Bu yazıda önce kısaca altın oran hakkındaki bilgilerimizi güncelleyelim sonra da plastik oran ve Harris spirali ile tanışalım.

İki parçaya bölmek istediğiniz bir doğru parçasına sahip olduğunuzu hayal edin. Bu doğruyu A ve B biçiminde büyük ve küçük parçalara bölerseniz, iki parçanın toplamının büyük parçaya bölümü, büyük parçanın daha küçük parçaya bölünmesine eşit olur. Yani (A + B) / A = A / B sonucunu elde ederiz. Bu sonuç altın orana eşittir.
Altın oran Yunanca phi (φ) harfi ile gösterilmektedir. Değeri ise φ = (1 + √5) / 2 = 1.6180339887498…biçimindedir. Altın orana φ denmesinin nedeni de aslında onu kompozisyonlarında kullanan Yunan heykeltıraş Phidias’a (MÖ 490-430) bir göndermedir. Phidias’ın adı Yunancada φ harfi ile başlar. Altın oranın en güzel özelliklerinden birisi öz benzerliğidir. Bunun için de altın dikdörtgen kavramını anlamanız gerekir.
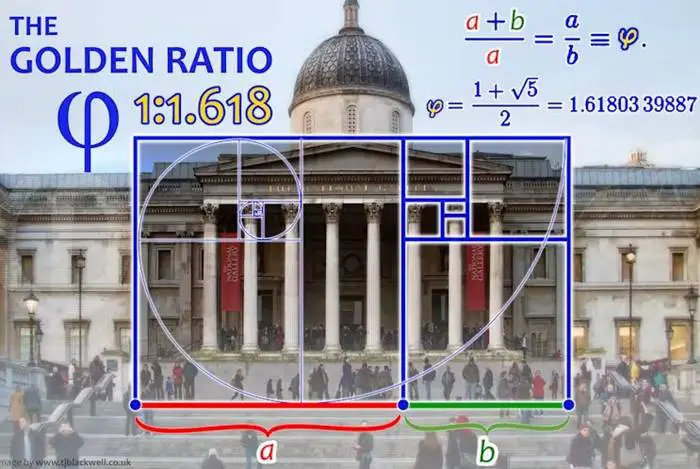
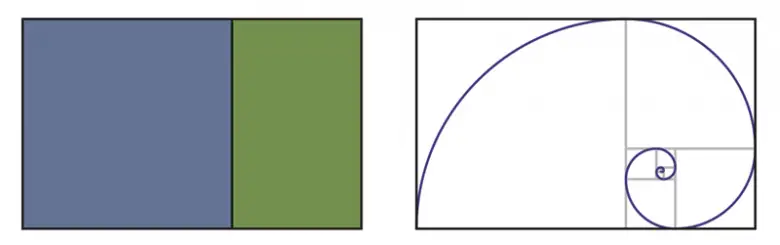
Altın dikdörtgen kenarları altın oran ile uyumlu olan bir şekildir. Diğer bir deyişle bu dikdörtgenin uzun kenarı, kısa kenarın yaklaşık 1.618 katı büyüklüğündedir. Altın dikdörtgenden bir kare çıkarırsanız geriye kalan kısım da altın orana uygun olacaktır. Bu işi yeterince tekrarlarsanız matematikçilerin en sevdiği şekillerden biri olan aşağıda da göreceğiniz bir altın bir spiral çizebilirsiniz.
Plastik Oran Nedir?
Estetik ve güzellik ölçütü olarak nitelendirilen biraz da abartılı bir üne sahip olan bu oran iddia edildiği kadar mucizeler ile ilişkili olmasa da yine de ilginç bir çok özelliği içeriğinde barındırır. Bu nedenle matematikçilerin her daim ilgisini çeker. Ancak altın oranın ünü aslında onun kardeşlerinden biri olan ve bir çok kişinin adını duymadığı plastik oranı gölgede bırakır.
Cebirsel sayılar, katsayıları tamsayılar olan bir polinomun kökü olarak ifade edilebilen sayılardır. Örneğin tüm rasyonel sayılar aynı zamanda bir cebirsel sayıdır. Sonuçta hepsi nx-m=0 biçimindeki bir polinomun kökleridir.
Bu noktada aslında bir matematikçi için, diğer cebirsel sayılarla altın oran örneğinde gördüğümüz gibi ilginç spiraller oluşturup oluşturamayacağınızı merak etmek doğal bir durumdur. Şaşırtıcı olmayan bir şekilde (aksi takdirde, bu makaleyi yazmıyor olurduk), güzel resimlere yol açan başka sayılar da var. Bunlardan bir tanesi plastik oran olarak bilinmektedir.
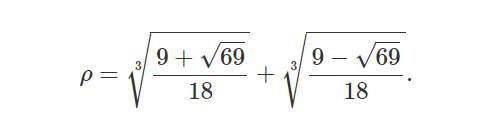
Plastik oran, x3 = x + 1 denkleminin çözümünde karşımıza çıkar ve ρ = 1.3247179… biçiminde bir açılama sahiptir. Tam karşılığı ise aşağıdaki formülde gördüğünüz gibidir. Kenar uzunlukları plastik orana uygun dikdörtgenler de çizebilirsiniz. Sonrasında bu şekillerden aynı altın oranda olduğu gibi bir kare çıkartırsanız geriye kalan dikdörtgenler yine plastik orana uygun olacaktır.
Ortaya çıkan her kareye iki yay çizip aynı parçalama işlemine devam edersek bu sefer ortaya daha ilgi çekici bir şekil çıkacaktır. ( Yaylar aynı hizada olacak şekilde seçilmelidir.). İşte bu şekil Harris spirali olarak bilinmektedir.
Harris Spirali İle Tanışalım
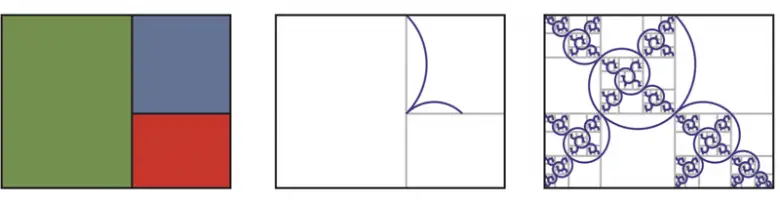
Matematikçiler genellikle yeni şeyler bulmayı severler. Bu bazen bir teorem olur bazen sadece bir çizim. Altın orandan ilham alan meraklı ve yaratıcı matematikçilerden birisi de Edmund Harris. Edmund Harris’de daha önce yukarıdaki plastik oran ile ilgili çalışmayı yapan kişi. Sonuçta da kimsenin çizmediği hoş bir fraktal eğri keşfetmiş ve bu eğriye adını vermiş durumda.

Gördüğünüz gibi altın oran matematikte varılacak son nokta değil tam tersine yaratıcı zihinler için bir başlangıç noktasıdır. Belki de polinom köklerine saklanmış başka etkileyici eğriler de vardır. Onları keşfetmek için de başka yaratıcı matematikçiler er ya da geç ortaya çıkacaktır. Kim bilir, belki de bunlardan birisi de siz bile olabilirsiniz. Neden olmasın? Ayrıca bu yazımıza da göz atmak isteyebilirsiniz:
Kaynaklar ve İleri Okumalar:
- The golden ratio has spawned a beautiful new curve: the Harriss spiral;yayınlanma tarihi: Bağlantı: https://www.theguardian.com
- Plastic number; https://en.wikipedia.org/
- Konu ile ilgili güzel bir video izlemek isterseniz: The Plastic Ratio – Numberphile; https://www.youtube.com/watch?v=PsGUEj4w9Cc
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel