Matematikte, Markov Zinciri, Markov özelliğine sahip bir stokastik süreçtir. Ancak elbette bu tanım konuya hakim olmayanlar için oldukça kafa karıştırıcı ifadeler içermektedir. Bu nedenle adım adım ilerlemek faydalı olacaktır.

Olasılık teorisinin kökleri şans oyunlarına dayanır. Buna göre adil bir madeni para atılırsa, yazı gelme olasılığı her zaman 1/2’dir. İkinci bir para atarsak, sonucun ilk atışımız ile hiçbir ilgisi yoktur. Bu bağımsızlık ilkesi bileşik olasılıkları hesaplamayı kolaylaştırır.
Adil bir parayı iki kez havaya atarsanız, her iki seferde de yazı gelme olasılığı basitçe 1/2×1/2 veya 1/4’tür. Daha genel olarak, iki bağımsız olayın p ve q olasılıkları varsa, her iki olayın birleşik olasılığı çarpımları pq olacaktır. Ancak, hayatın tüm yönleri bu ilkeye uymaz.
Yağmurlu bir günün olasılığının 1/3 olduğunu varsayalım. Bu, iki gün üst üste yağmur yağma olasılığının 1/3×1/3=1/9 olduğu anlamına gelmez. Monopoly oyununu düşünün. Zar atmak tahtada kaç adım ilerleyeceğinizi belirler, ancak sonunda nerede duracağınız nereden başladığınıza bağlıdır.

Zaman içerisinde önceden kestirilemeyecek şekilde gelişen süreçlere Stokastik yani Rastgele süreçler denir. Bu süreçlerde gelecekteki olayların olasılıkları sistemin mevcut durumuna bağlıdır ve olaylar birbirine bağlandıkça bir Markov zinciri oluştururlar.
Markov Zincirleri Nedir?
Uygun bir Markov zinciri olarak kabul edilmek için, bir sistemin aralarında geçişler bulunan bir dizi belirgin duruma sahip olması gerekir. Basitleştirilmiş bir hava durumu tahmini modeli sadece üç duruma sahip olabilir: güneşli, bulutlu ve yağmurlu. Bu durumda dokuz olası geçiş vardır.
Noktalar ve oklardan oluşan bir diyagram, bir Markov zincirinin yapısını gösterir. Noktalar durumları temsil eder; oklar geçişleri belirtir. Her ok, o geçişin olasılığını veren ilişkili bir sayıya sahiptir. Bu sayılar olasılıklar olduğundan, 0 ile 1 arasında yer alır. Ayrıca bir noktadan çıkan tüm olasılıklar tam olarak toplam 1’e eşit olmalıdır. Belirli dizinin olasılığını hesaplamak için, karşılık gelen geçiş oklarıyla ilişkili olasılıkları çarpmanız yeterlidir.
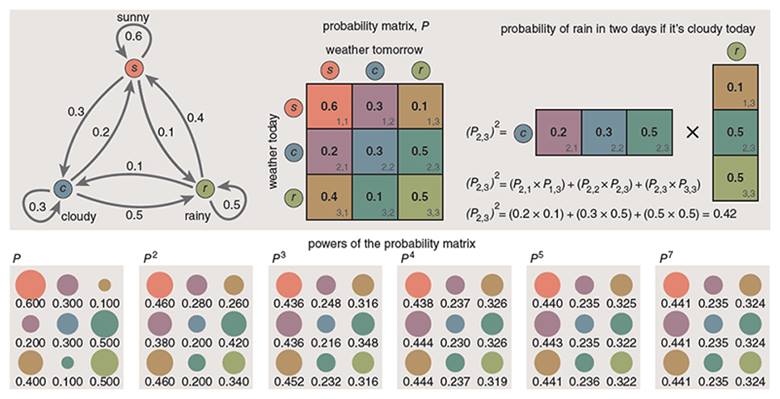
Üç durumlu bir Markov zinciri için geçiş olasılıkları, üçe üç matriste düzenlenebilir. Çizimde gösterildiği gibi, çok aşamalı geçişleri hesaplama süreci matris çarpımına eşdeğerdir. Matrisin kendisi ( P diyelim) yarının hava durumunu tahmin etsin. P × P veya P 2 çarpımı yarından sonraki gün için hava durumu olasılıklarını verir. P 3 üç gün sonraki olasılıkları tanımlar, vb. Tüm gelecek bu tek matristen ortaya çıkar.
Markov zincirleri son derece yararlı araçlardır ve ekonomi, biyoloji, bilgisayar, pazarlama ve daha pek çok alanda kullanılır. Örneğin, Google’ın kurucuları Larry Page ve Sergey Brin tarafından tasarlanan PageRank algoritması, durumları World Wide Web’in sayfaları olan bir Markov zincirine dayanmaktadır. Geçişler sayfalar arasındaki bağlantılardır. Algoritmanın amacı, her web sayfası için bağlantıları rastgele takip eden bir okuyucunun o sayfaya ulaşma olasılığını hesaplamaktır.
Markov zinciri ile ilgili bir örnek
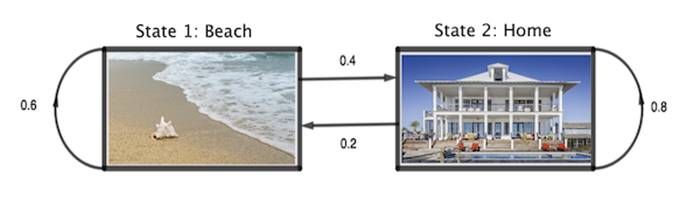
Yukarıdaki resim Markov zinciri kullanılarak modellenebilen bir duruma örnektir. Resimden de anlaşıldığı gibi iki durumumuz var: Sahil (durum 1) ve Ev (durum 2). Diyelim ki yazlığa gittiniz. Bu durumda günün tüm saatlerini bu iki durumdan birinde geçirmeyi tercih ediyorsunuz.
Bu durumda bazı olasılık hesaplamaları yapılmış ve sahildeysek, bir saat sonra hala sahilde kalma olasılığımız 0,6 ve bir saat sonra eve gitme olasılığımız 0,4 ve eğer evdeysek bir saat içinde evde kalma olasılığımız 0.8, kumsala gitme olasılığımız 0.2 biçiminde belirlenmiş olsun.
Şimdi bunları matris formunda göstermemiz gerekiyor. Markov zincirimiz için aşağıdaki matrisi tanımlayabiliriz. Burada solda gördüğünüz matriste m11, 1. durumda başlayıp, 1. durumda kalmayı, m12, 1. durumda başlayıp 2. duruma geçmeyi vb gibi ifade etmektedir. Sonrasında verilenleri yerlerine yerleştirirsek sağ taraftaki matrisi elde ederiz.
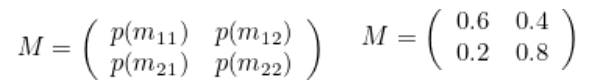
İki Saat Sonra Nerede Olacağız?
Bu aslında oldukça zor bir soru. Ancak Markov zinciri sayesinde bu soruya da bir cevap vermemiz mümkün. Güne sahil ile başlayan biri için, iki saat sonra sahilde olma olasılığı, tüm zaman boyunca sahilde kalma olasılığı artı eve gidip sahile geri dönme olasılıkları toplamı kadar olacaktır.
Burada, birinin gelecekte nerede olacağını hesaplamak için Markov zincirlerinin faydasını görüyoruz. Tek yapmamız gereken yukarıdaki matrisin karesini almak, diğer bir deyişle kendisi ile çarpmak olacaktır. Bu durumda, matris çarpım kurallarını kullanırsak bu bize aşağıdaki sonucu verecektir.
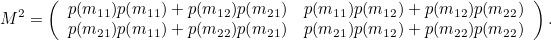
Yukarıdaki çarpımda sol üstte az evvel bahsettiğimiz, birinin güne sahilde başlayıp iki saat sonra sahilde olma olasılığının yer aldığını fark edeceksiniz. Bundan sonrasında, başlangıç ve bitiş durumunu temsil etmek için ok gösterimini kullanacağız. Okun solu ilk bulunduğumuz yeri, sağı ise ikinci bulunduğumuz yeri gösteriyor. Bu durumda çarpım matrisimizin sonucu aşağıdaki gibi olacaktır.
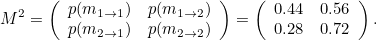
24 Saat Sonra Nerede Olacağız?
Bu durumda güne sahilde başlayan birinin iki saat içinde sahilde olma olasılığının 0.44 olduğunu görebiliriz. Aynı şekilde eve giren birinin iki saat sonra sahilde olma olasılığı 0.28’dir. İstersek, gelecekteki herhangi bir saat içinde birisinin nerede olacağını bulmak için matris çarpımı ile işe devam edebiliriz. Örneğin, birinin 24 saat içinde nerede olacağını görmek istersek, matris çarpımları yaparak şunu elde ederiz.
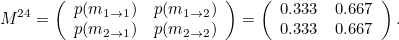
Aslında burada ilginç bir sonuçta elde ettik. Bunu aşağıda görebilirsiniz. Aslında birinin güne nerede başladığının pek de önemi yok. Güne ister sahilde ister ise evde başlamış olsunlar, 24 saat içinde sahilde olma ihtimali 0,333 kadardır. Yani aradan geçen saat sayısı arttıkça bu senaryodaki kişinin zamanının 1/3’ünü kumsalda ve 2/3’ünü evde geçirdiği sonucuna varabiliriz. Çok da kötü bir hayat sayılmaz.!
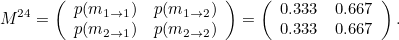
Bu örnek size Markov zincirlerinin nasıl çalıştığına dair basit bir mantık verebilir. Ancak unutmayın, işin teorik kısmı bundan çok daha fazlasıdır. Kısacası daha keşfetmeniz gereken çok şey var!
Kaynaklar ve ileri okumalar:
- Markov , A.. (2006). An Example of Statistical Investigation of the Text Eugene Onegin Concerning the Connection of Samples in Chains. Science in Context. 19. 591 – 600. 10.1017/S0269889706001074.
- Andrey Markov & Claude Shannon Counted Letters to Build the First Language-Generation Models. Yayınlanma tarihi: kaynak site: Bağlantı: Andrey Markov & Claude Shannon. Counted Letters to Build the First Language-Generation Models
- Andrey Markov’s Brilliant Ideas are still a Driving Force. (Erişim Tarihi: 10.03.2021); Kaynak site: Thats Math. Bağlantı: Andrey Markov’s Brilliant Ideas are still a Driving Force.
- Life on the beach with Markov chains; yayınlanma tarihi: 29 Kasım 2021; Kaynak site: Plus Math. Bağlantı: Life on the beach with Markov chains;
Matematiksel