Matematikte hangi taşı kaldırsak altından Leonhard Euler adı çıkıyor diye düşünüyorsanız haklısınız! Üstelik sadece matematik de değil geometride de adı pek çok yerde karşımıza çıkacaktır. Bunlardan biri de bu yazıda ele alacağımız Euler doğrusu ve beraberinde dokuz nokta çemberidir.

Lisede temel geometri eğitimi alırken üçgen ile ilgili bir çok özel nokta ile tanışmıştık. Bunlardan en temel olan iç teğet çemberin merkezi, diklik merkezi, ağırlık merkezi ve dış teğet çemberin merkezi olarak aklınıza gelebilecektir.
Eğer tam olarak aklınıza gelmiyorsa kısaca anımsatalım. Herhangi bir üçgende kenar orta dikmeler ( yani kenarların ortalarından geçen dik çizgiler tek bir noktada kesişir. Kesiştikleri bu noktaya dış teğet çemberin merkezi ya da çevrel çember denir.
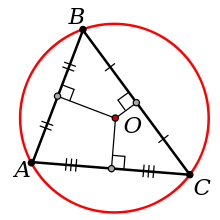
Benzer bir biçimde herhangi bir üçgenin üç kenarortayı da bir noktada kesişir. Kenarortayların kesiştikleri nokta ağırlık merkezidir. Son olarak herhangi bir üçgenin üç yüksekliği de tek bir noktada kesişir ve bu noktaya da diklik merkezi adı verilir.
Şimdi aşağıdaki görsele bakalım. Bu görselde yukarıda adı geçen tüm merkezlerin aslında tek bir çizgi üzerinde yer aldığını görüyorsunuz. Tüm üçgenler için böyle bir çizginin var olması oldukça beklenmedik bir durumdur. Peki ama bunun bir anlamı var mıdır? Bu sorunun cevabını 1763’te matematikçi Leonhard Euler (1707-1783) verecekti.
Dokuz Nokta Çemberi Nedir?
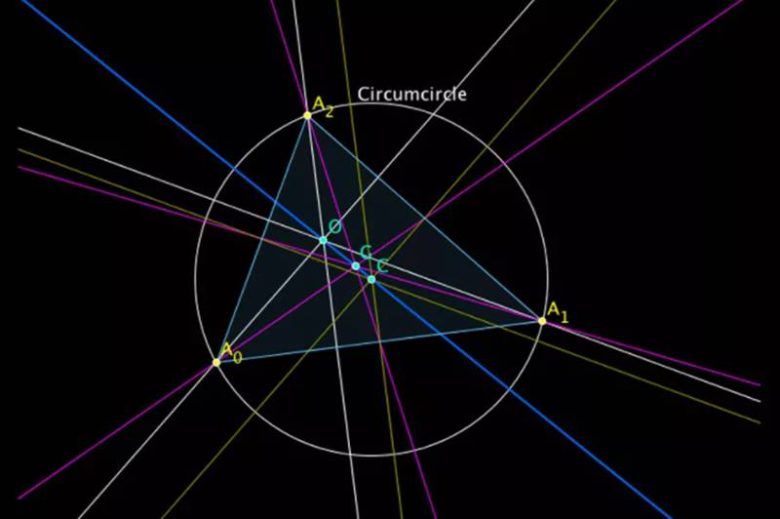
Doğrusal olmayan üç noktadan bir çember çizilebildiğini biliriz. Aynı çemberde bir dördüncü nokta ortaya çıkarsa bu oldukça dikkate değerdir. Hele ki aynı çember üzerinde dokuz nokta olduğunu gösterebilirsek bu gerçekten önemli bir başarı olur.
Aslında aynı çember üzerinde yer alan üçten fazla nokta bulmak matematikçiler için uzun süre devam eden bir uğraşı olmuştur. 18. ve 19. yüzyıl matematikçileri, analiz ve cebirle çok ilgilenmelerine rağmen, geometrik yapıları da keşfetmeye devam ettiler. Sonucunda 1765’te Leonhard Euler, bir üçgenden oluşturulan dokuz noktanın bir çember üzerinde yer aldığını gösterdi. Dokuz nokta çemberinin üzerinde bulunan noktaların altısının, kenarların orta noktaları ve yüksekliklere ait olduğunu ispatladı.
1820’de, Charles Julien Brianchon ve Jean Victor Poncelet tarafından konuyla ilgili bir makale yayınlandığında geri kalan noktaların da aynı çember üzerinde olduğu kanıtlanacaktı. Daha sonra işin içine Alman matematikçi Karl Wilhelm Feuerbach (1800-1834) dahil oldu. Kendisi de 1822’de konuya ilişkin bir teorem ileri sürdü. Bu çalışmalarının sonucunda günümüzde adı ile anılan Feuerbach çemberi ve Feuerbach noktası ile konuya katkı sağladı.
Euler Doğrusu Nedir?
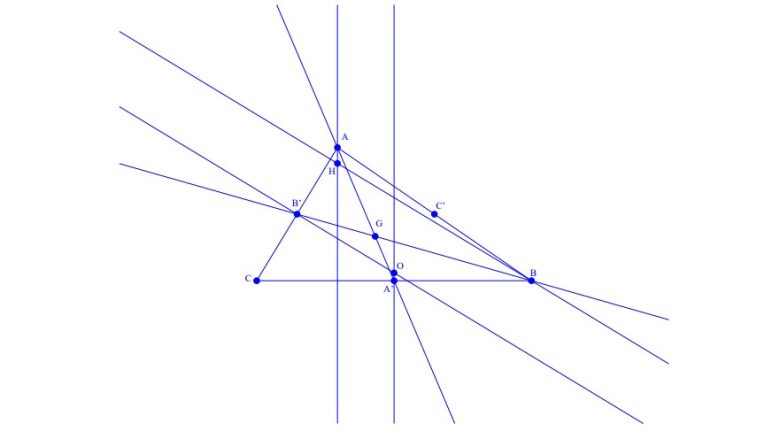
Bir dokuz nokta çemberi tanımladıysak elimizde bu çemberin de bir merkezi olmalıdır. İşte bu merkez yazının başında sizlere tanıttığımız Euler doğrusu ile ilginç bir ilişki içindedir. Üçgenin ağırlık merkeziyle diklik merkezini birleştiren doğrunun orta noktası dokuz nokta çemberinin merkezidir. Üçgenin kenarlarına orta noktalarından çizilen dikmeler de bir noktada kesişir. Bu nokta aynı zamanda üçgenin üç tepe noktasını içeren dış çemberin de merkezidir. Euler dokuz nokta çemberinin çapı işte bu dış çemberin yarıçapına eşittir.
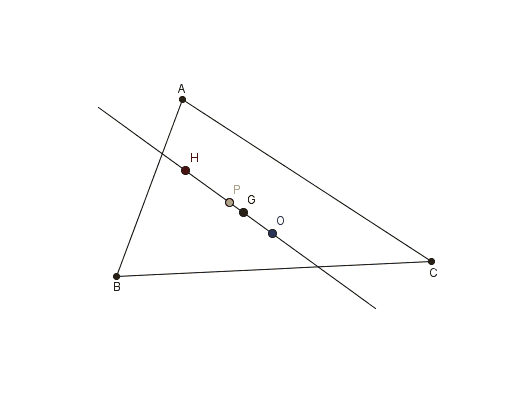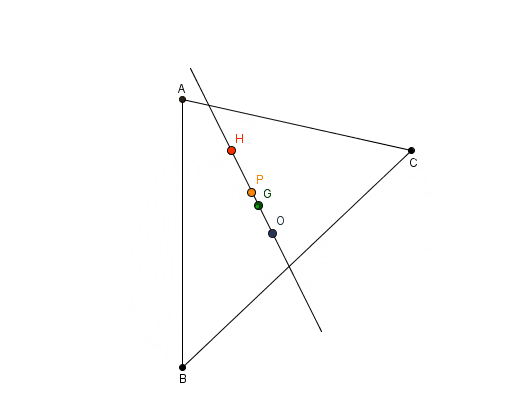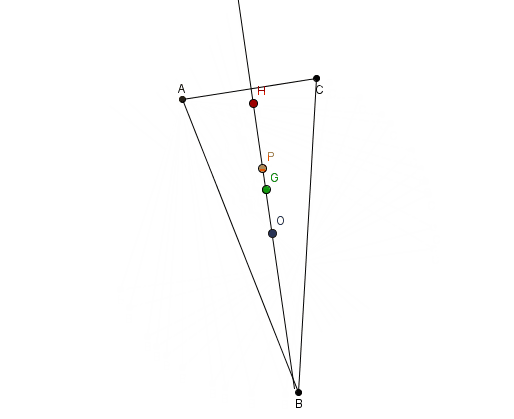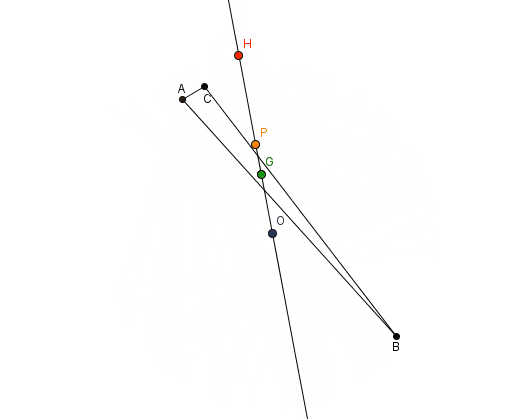
Ayırca tüm bu noktaları bir arada düşündüğümüz zaman karşımıza şaşırtıcı bir sonuç çıkar. Bu 4 nokta doğrusaldır yani aynı doğru üzerindedir. Bu sonuç tarafından keşfedildiği içinde dört noktayı üzerinde barındıran doğruya Euler doğrusu denir. Euler doğrusunun önemli bir sonucu, ağırlık merkezi, diklik merkezi ve çevrel çemberin merkezinin herhangi biri hakkındaki bilginin diğer ikisi hakkındaki bilgiden türetilebilmesidir. ( İspatına bu yazıdan göz atabilirsiniz.)
Kaynaklar ve ileri okumalar:
- What is Euler’s line?; Bağlantı: https://www.quora.com/
- Painting – Nine-Point Circle; Bağlantı: https://americanhistory.si.edu/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel