Doğrusal programlama, belirli bir gereksinimler listesinden olası en iyi çözümü belirlemek için kullanılan matematiksel bir yöntemdir. Para, enerji, insan gücü, zaman gibi sınırlı kaynakların tahsisinde en iyi çözümü bulmak için kullanılır. Çoğu durumda, doğrusal programlamadan ihtiyaç duyulan “en iyi sonuç”, maksimum kar veya en düşük maliyettir. Bu nedenle genellikle doğrusal optimizasyon da denir.

Doğrusal programlama ifadesindeki doğrusal kelimesi bir problemde kullanılan birinci derecedeki çeşitli değişken türleri arasındaki ilişkiyi ve programlama kelimesi ise bize bu problemleri çözmek için gereken adım adım prosedürü anlatır. Doğrusal programlama çeşitli problemlere bir çözüm üretmek için kullanılır türlerini çözmek için özellikle ekonomi, mühendislik, askeriye ve eğitim sektöründe yer alan optimizasyon probleminin çözümünde çokça kullanılır.
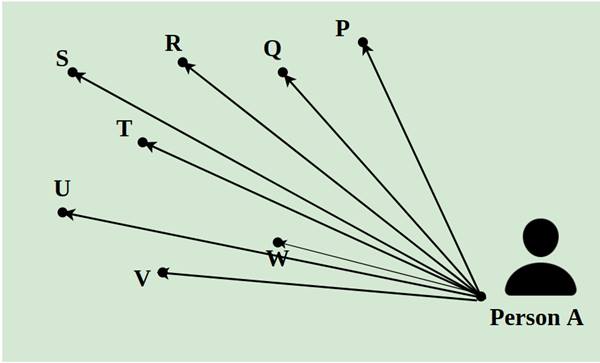
Bir teslimatçının bir günde 8 paketi şehrin farklı yerlerine teslim etmesi gerektiğini varsayalım. A’dan tüm paketleri alıp P, Q, R, S, T, U, V ve W noktalarına teslim etmesi gerekiyor. Aralarındaki mesafe aşağıdaki resimde gösterildiği gibi çizgiler kullanılarak belirtiliyor. Teslimatçının izlediği en kısa yol Doğrusal Programlama kavramı kullanılarak hesaplanır. Birçok farklı doğrusal programlama problemi vardır ancak bu makalede diyet problemini ele alacağız.
Diyet Problemleri Nedir?
Her insan, cebindeki paranın daha azını kullanarak, vücudun ihtiyacı olan besini almak ister. Yiyeceklerin mevcudiyetine ve fiyatlarına bağlı olarak minimum maliyeti elde etmek için diyete dahil edilecek farklı türdeki bileşenlerin sayısını hesaplama problemine de diyet problemi denir.
Diyet problemleri ilk olarak 1939 yılında George Stigler tarafından doğrusal programlama kullanılarak çözülmüştür. Stigler, modelinde vücudun ihtiyacı olan 16 temel gıda ve bu gıdaları içinde barındıran 77 çeşit yiyeceği kullanmıştır. Aynı problemi 1945 yılında 80 değişik yiyecek türünü kullanarak tekrar çözmüştür.
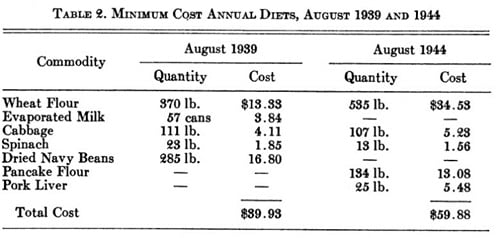
Aşağıda bir örnek verdiğimiz diyet problemleri, yarım asırdan fazla bir zamandır, ekonomistleri üzerinde en çok düşündüren konulardan biri olmuştur.
Doğrusal Programlama İle İlgili Bir Örnek: Diyet Problemi
Ayşe sporu ciddi bir uğraş olarak görür. Her gün spor salonuna gider, yediğine ve içtiğine de dikkat eder. Sağlıklı ve zinde kalmak için vitamin ve mineralleri her ay doğru miktarlarda alması önemlidir. Bu miktarları ise koçu belirler. Koçun dediğine göre her ay en az 120 mg vitamin ve 880 mg mineral alması gerekir. Ayşe, bu diyete uymak için 2 farklı besin takviyesi alır. Birisi katı haldeki Solido, diğeri sıvı haldeki Liquex. Ancak bir sorunu vardır. Koçunun söylediklerini yerine getirmek için hangisinden ne kadar almalıdır?
Bunun için Ayşe elbette iki ürünün de içeriğini inceler. Solido kutusunun üzerinde yazanlara göre içinde 2 mg vitamin 10 mg mineral; Liquex’de ise 3 mg vitamin 50 mg mineral vardır. 30 kutu Solido ve 5 şişe Liquex alır. Sonra hesabını yapar. Aldıklarına göre elinde toplam 75 mg vitamin (2 x 30 = 60 ve 3 x 5 = 15; 60+15=75); 550 mg mineral (10 x 30 + 50 x 5= 550 ) olduğunu görür.
| Solido | Liquex | Gereken Miktar | |
| Vitamin | 2 mg | 3 mg | 120 mg |
| Mineral | 10 mg | 50 mg | 880 mg |
Tanya koçun dediği miktarı düşününce, 10 kutu Solido ve 10 şişe Liquex daha almaya karar verir. Yeniden hesap yapınca elinde 125 mg vitamin ve 1150 mg mineral vardır. Ancak bu sefer gereksiz masraf yapmıştır. Sonuçta koçun isteğinden bile fazla vitamin ve minerale şu an sahip olmuş durumdadır.
Ayrıca problemin olası birden çok çözümü olduğunu fark eder. Sonuçta sadece 88 kutu Solido alsa 176 mg vitamin ve 880 mg mineral alacaktır. Bu da koçun söylediği miktarı karşılayacaktır. Ya da sadece 40 şişe Liquex alsa120 mg vitamin ve 2000 mg mineralde istenilen için yeterlidir. Asıl soru şurada başlar. Tüm bu olasılıkların içerisine harcanacak parayı optimize etme sorunu girerse uygun çözüm hangisi olur?
Problemin içine Optimizasyon Karıştıralım
İlaçların her ikisinin de fiyatları 5 dolardır. Dolayısıyla çözüm olarak bulunan (40,15), (88,0) ve (0,40) değerlerinin maliyetleri sırasıyla 275, 440 ve 200 dolar olacaktır. İlk bakışta Solido almayıp 40 şişe Liquex almak en uygun sonuç gibi görünmektedir. Ama ya daha da iyisi mevcutsa? İşte bu esnada Ayşe’nin aklına grafik çizmek gelir. Gördüğünüz gibi (48,8) noktasında yeni bir çözüm mevcut.
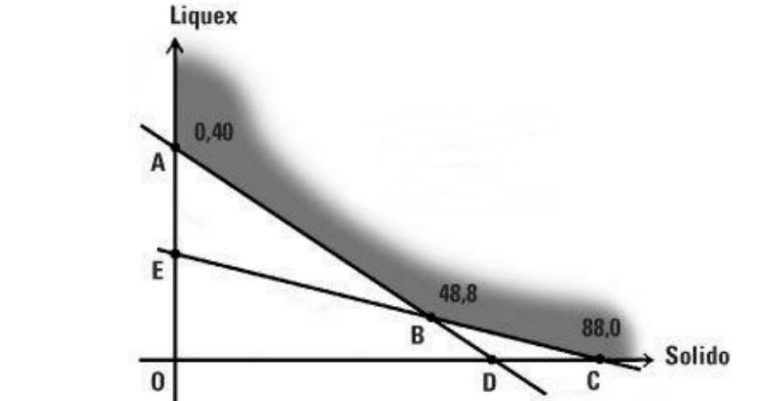
Yani 48 kutu Solido ve 8 şişe Liquex alırsa koçun isteğini tam sağlayan (120 mg vitamin ve 880 mg mineral) miktarı almış olacaktır. Fakat bunun maliyeti ise 280 dolardır. Yani ya parayı düşünüp 200 dolara 40 şişe Liquex alabilir. Ya da tam alması miktarı düşünüp 280 dolara 48 kutu Solido ve 8 şişe Liquex alabilir. Siz olsanız ne yapardınız?
Muhtemel siz de parayı düşünürdünüz. Zaten bu tip problemlerde optimum çözüm, genelde de paraya bağlıdır. Doğrusal programlamanın temel amacı kârı maksimize edecek optimum çözüme ulaşmaktır. Klasik diyet problemiyle başlayan sorumuz bizi doğrusal programlamanın mantığını anlamaya kadar götürür.
Doğrusal Programlama Problemleri Nasıl Çözülür?
Doğrusal programlama problemini çözmek için en yaygın yöntemlerden biri simpleks yöntemidir. George Dantzig, doğrusal programlama problemlerinin çözümünde kullanılan simpleks algoritmasını geliştirmesi ile tanınan ünlü bir matematikçidir. Good Will Hunting ya da Türkçe adıyla Can Dostum filmini izleyenlerin hatırlayacağı bir sahne vardır.

Bu sahnede bir gün profesörlerden biri, ofisinin dışındaki tahtaya zorlu bir matematik problemi yazar. Herhangi bir üniversite eğitimi almamış temizlikçi ise bu soruyu kolayca çözer. Bir çok kişinin bilmediği şey filmin bu sahnesinin kısmen gerçeğe dayanmasıdır. Filmin amaçları doğrultusunda bir miktar değişiklik olsa da daha sonra ünlü bir matematikçi olacak olan George Dantzig hikayenin asıl kahramanıdır.
Grafik Yöntemi, doğrusal programlama problemlerinin çözümünde kullanılan Simplex yönteminden farklı bir yöntemdir. Adından da anlaşılacağı gibi bu yöntem, verilen doğrusal programlama problemlerini çözmek için grafikleri kullanır.
Kaynaklar ve ileri okumalar:
- Maths in a minute: Some basic linear programming; Yayınlanma tarihi: 26 Nisan 2017; Bağlantı: https://plus.maths.org/
- Sahiner, Ahmet & BUZKAN, Gamze. (2014). Fuzzy Hedef Programlamanın Özel Bir Diyet Problemine Uygulanması. Süleyman Demirel Üniversitesi Fen Bilimleri Enstitüsü Dergisi. 14. 10.19113/sdufbed.71779.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel



