Dünya çok hızlı bir şekilde dijitalleşiyor. Artık sadece fiziksel dünyada bir kimliğimiz yok. Aynı zamanda çevrimiçi ortamlarda da bizi temsil eden bilgilerimiz var. Bu da dijital ortamda bizi temsil eden verilerin güvenliğini sağlamamız gerektiği anlamına geliyor. Fiziksel dünyada kendinizle ilgili başkalarının bilmesini istemediğiniz şeyleri saklamak kolaydır. Peki çevrimiçi ortamda gizliliğimizi ve güvenliğimizi nasıl sağlıyoruz?

Çevrimiçi ortamlarda erişmek istediğimiz şeyler için zaman zaman çeşitli bilgiler vermemiz gerekebiliyor. Çünkü bizden bilgi isteyen tarafın da ne için kendilerine başvurduğumuzu bilmesi gerekiyor. Yani onlar da kendi güvenlikleri için bunu yapmak durumunda kalıyor. Fakat biz de bilgilerimizi vermek istemeyebiliyoruz. Sonuçta paylaştığımız bilgilerle ne yapacaklarını bilemiyoruz.
İşte bu noktada karşımıza matematiğin sunduğu harika bir çözüm çıkıyor: Sıfır bilgi ispatları. İsim kulağa biraz tuhaf gelmiş olabilir. Çünkü matematiksel ispatların bir dolu bilgi üzerinden yapıldığını biliyoruz. O halde nasıl sıfır bilgiyle ispat yapılabilir öyle değil mi? Gelin, matematik ve bilgisayar biliminin ürünü olan bu ilginç kavramı birlikte inceleyelim.
Sıfır Bilgi İspatı Nedir?
1980’lerde Shafi Goldwasser, Silvio Micali ve Charles Rackoff tarafından ortaya atılan sıfır bilgi ispatları, dijital iletişimde gizlilik ve güvenlik hakkındaki düşüncelerimizde devrim yaratmıştır. Bununla da kalmayıp modern kriptografinin önünü açmış ve ispatlara bakış açımızda bir değişikliğe sebep olmuştur. Peki sıfır bilgi ispatları tam olarak nedir?

Aslında sıfır bilgi ispatları için kısaca, bir ifadenin geçerliliğini ifadenin kendisinin geçerliliğinden başka bir şey ortaya koymadan kanıtlama yöntemidir diyebiliriz. Ancak bu tanımı biraz daha açarak anlatmak daha güzel olacaktır. Diyelim ki birisine bir şeyi ispatlamak istiyorsunuz. Fakat ispat yönteminiz biraz farklı. Amacınız, karşınızdakine ispatlamak istediğiniz şeyin doğru olduğu dışında başka hiçbir bilgi vermemek. İşte sıfır bilgi ispatı budur.
İspatlamak istediğimiz şey hakkında hiçbir bilgi vermeden onun doğruluğunu ispatlamak imkansızmış gibi görünebilir. Çünkü ispat deyince hepimizin aklına satır satır işlem ve doğrulama yaptığımız matematiksel ispatlar geliyor. Ve bir matematiksel ispat, bir ifadenin doğruluğunun eksiksiz, adım adım gösterilmesidir. Matematiksel bir ispatta her şey açıkça ortadadır ve doğrulanabilirdir. Sıfır bilgi ispatları ise doğrulayıcı gerektiren minimum bilgi ispatlarıdır. Gizliliği korumak için ortaya atılmıştır ve bu nedenle açık değildir.
Sıfır Bilgi İspatlarını Daha İyi Anlayabilmemiz İçin İki Örnek
Sıfır bilgi ispatları ilk ortaya çıktığında matematikçiler bu kavrama biraz şüpheyle yaklaştı. Ancak bu ispatların ne kadar etkili olduğunu görmeleri çok uzun sürmedi. Yine de sıfır bilgi ispatlarının tam olarak bir ispat olmadığını söylemek sanıyoruz yanlış olmaz. Çünkü bu ispatların çok az da olsa yanlış olma payı vardır. Fakat bu olasılık son derece (%0.00000…1, burada 100’den fazla 0 vardır) küçüktür ve ihmal edilebilir.
Örnek 1: Kırmızı-Yeşil Renk Körü Arkadaşınıza Topların Farklı Renkte Olduğunu Nasıl Kanıtlarsınız?
Diyelim ki elinizde tek farkları renkleri olan biri kırmızı diğeri yeşil iki top var. Arkadaşınız ise kırmızı-yeşil renk körü. Arkadaşınıza hangi topun kırmızı, hangi topun yeşil olduğu bilgisini vermeden bu iki topun farklı renkte olduğunu kanıtlamanız gerekiyor. Bunu nasıl kanıtlayabilirsiniz?

Arkadaşınızdan topları arkasında saklamasını isteyin. Arkadaşınız bu esnada topları elden ele değiştirebilir ya da değiştirmeyebilir. Bu iki seçenekten istediğini yaptıktan sonra size topları göstermesini isteyin. Siz topların rengi ayırt edebildiğiniz için arkadaşınızın topları yer değiştirip değiştirmediğini anlayabilirsiniz. Bu süreci hata yapmadan yeterince tekrar ettiğinizde arkadaşınız hangi topun ne renk olduğunu bilmeden topların farklı renkte olduğuna ikna olacaktır.
Örnek 2: Fiyat Açıklaması Yapmadan Kimin Daha Fazla Ödediğini Nasıl Bulursunuz?
Diyelim ki siz ve rakibiniz, aynı ürünleri aynı tedarikçiden aldığınızı keşfettiniz. Ve bu tedarikçinin ürünleri ikinizi de aynı fiyata satıp satmadığını merak ediyorsunuz. Ancak hem birbirinize rakip olduğunuzdan hem de tedarikçiyle fiyatı kimseye açıklamayacağınıza dair bir sözleşme yaptığınızdan ürünlere kilogram başına ne kadar ödediğinizi açıklayamıyorsunuz. Bu durumda tedarikçinin ürünleri aynı mı yoksa farklı fiyata mı sattığını nasıl öğrenebilirsiniz?
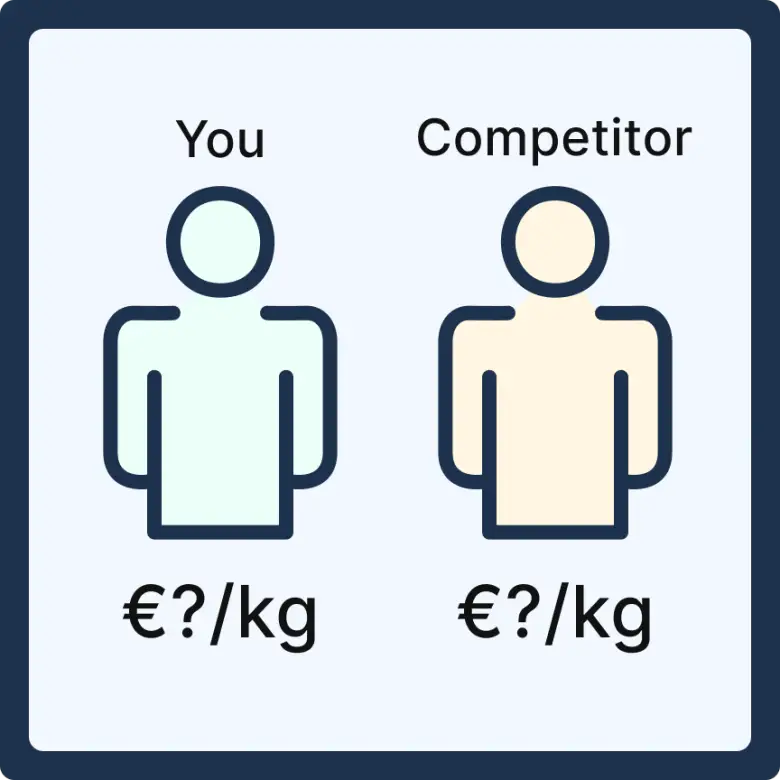
Bunun için şöyle bir yol izleyebilirsiniz. Diyelim ki ürünlerin kilogram başına piyasa fiyatı 100, 200, 300 veya 400 Euro’dan biri olabiliyor. Bu durumda üzerinde 100, 200, 300 ve 400 yazan, içine sadece minik bir kağıdın sığabileceği 4 tane kilitlenebilir kutuyu bir odaya yerleştiriyorsunuz.
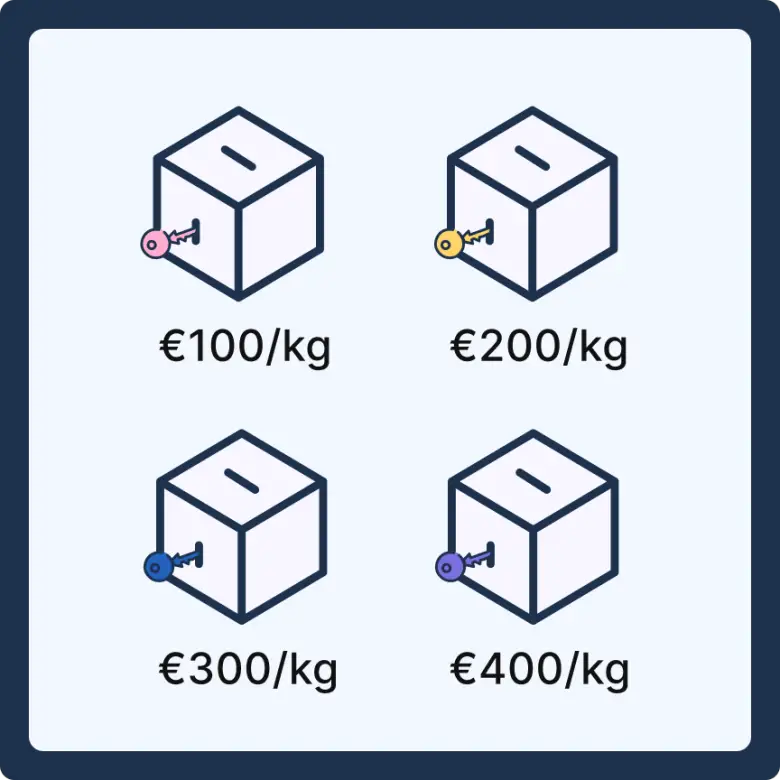
Odaya ilk önce siz, tek başınıza giriyorsunuz. Diyelim ki siz, kilogram başına 200 Euro ödüyorsunuz. Bu nedenle üzerinde 200 yazan kutunun anahtarını alıyor ve diğer anahtarları imha ediyorsunuz. Sonra da odadan çıkıyorsunuz.
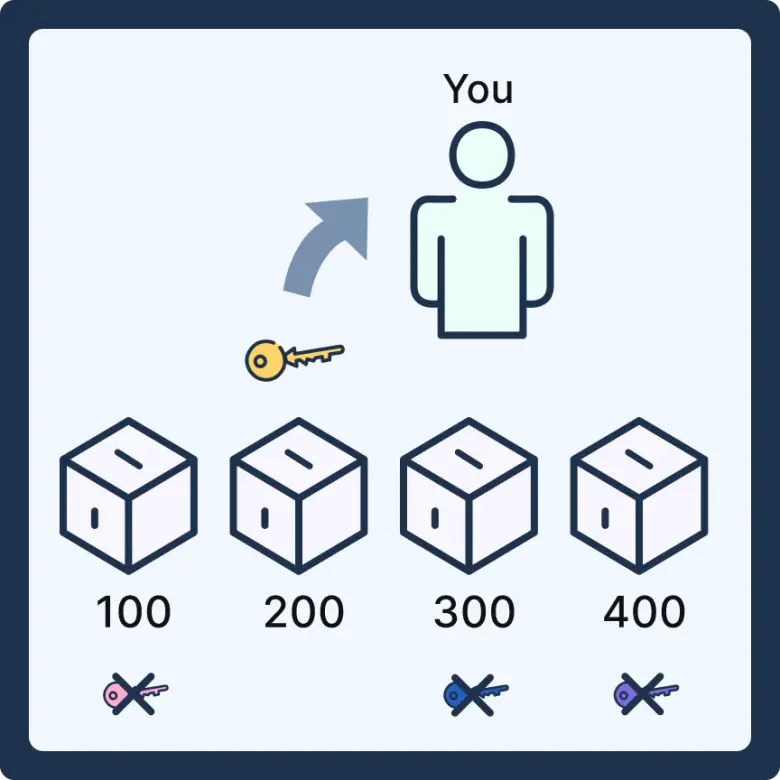
Siz odadan çıktıktan sonra rakibiniz elinde 4 kağıtla içeri giriyor. Rakibinizin elindeki bu 4 kağıdın 3’ünde çarpı işareti, 1’inde de tik işareti var. Diyelim ki rakibiniz de kilogram başına 300 Euro ödüyor. Bu nedenle de elindeki tik işareti olan kağıdı üzerinde 300 yazan kutuya atıyor. Çarpı işareti olan kağıtları ise birer tane olmak üzere diğer kutulara atıyor.
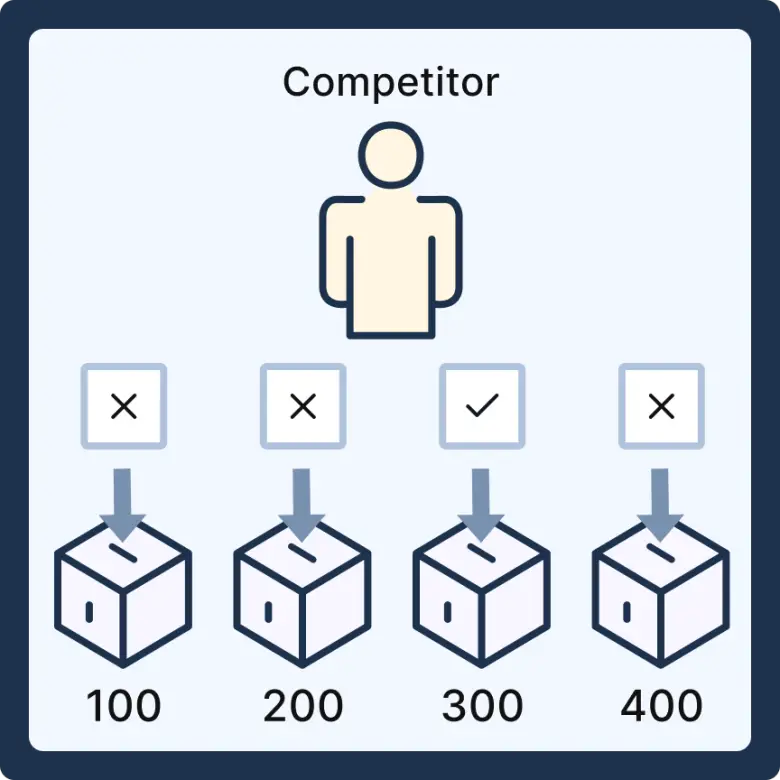
Daha sonra siz elinizde üzerinde 200 yazan kutunun anahtarıyla odaya giriyorsunuz. Elinizde bir tek o anahtar olduğu için 200 yazan kutunun kilidini açıyor ve çarpı işaretli kağıdı görüyorsunuz.
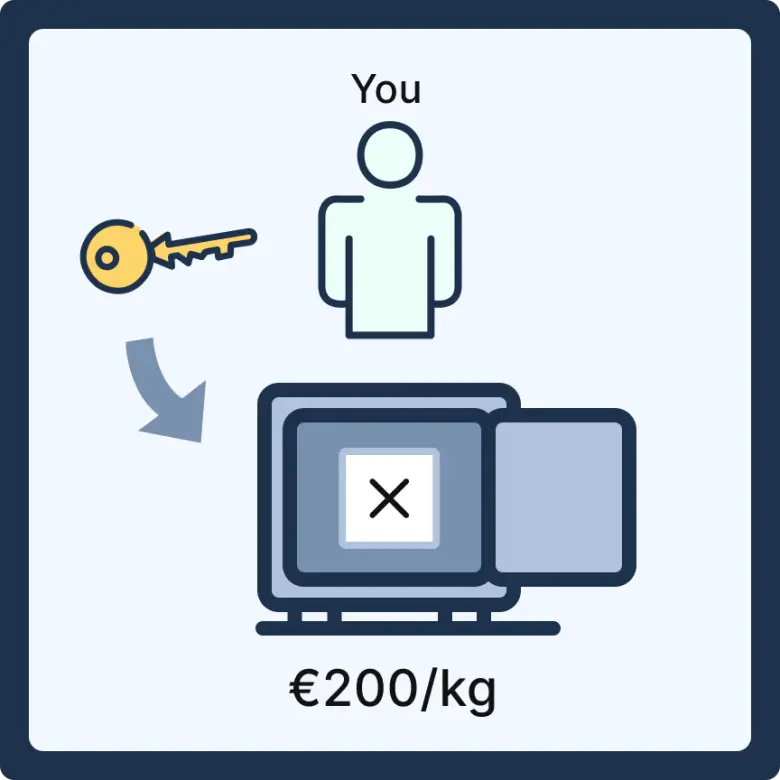
Odadan elinizde çarpı işareti olan kağıtla çıkıyorsunuz. Rakibiniz elinizde çarpı işareti olan kağıdı görünce tedarikçinin ürünleri size farklı bir fiyattan sattığını anlıyor. Ama size kaça sattığını bilmiyor. Benzer şekilde siz de üzerinde 200 yazan kutudan tik işaretli kağıt çıkmadığı için rakibinizin 200 lira ödemediğini biliyorsunuz. Ancak kaç Euro ödediğini de bilmiyorsunuz.
Sıfır Bilgi İspatlarını Günlük Hayatta Nerelerde Kullanıyoruz?
Buraya kadar anlattıklarımızla sıfır bilgi ispatları biraz teoride faydalıymış gibi görünmüş olabilir. Ancak günlük hayatta bu ispatlardan sürekli yararlanıyoruz. Dijital ortamda belge imzalamaktan tutun da çevrimiçi oyun oynamaya, kimlik doğrulama işlemlerinden blok zincir işlemlerine kadar birçok yerde sıfır bilgi ispatları sayesinde gizliliğimizi ve güvenliğimizi koruyoruz.
Ancak bu ispatların sadece dijital ortamlarda işe yaradığını söylemek yanlış olur. Öyle ki, 2016 yılında Princeton Plazma Fiziği Laboratuvarı ve Princeton Üniversitesi sıfır bilgi ispatlarını oldukça ilginç bir yerde kullandı. Gelecekteki nükleer silahsızlanma görüşmelerinden uygulanabilecek bir teknik geliştirdiler ve bunda da sıfır bilgi ispatlarından yararlandılar. Bu teknikte denetçiler, bir nesnenin gerçekten bir nükleer silah olup olmadığını anlayabilecekler. Fakat nesnenin gizli olabilecek iç işleyişini bilmeden ve ifşa etmeden bunu yapacaklar.
Sıfır bilgi ispatlarının fiziksel uygulama alanlarına bir başka örnekse DNA testidir. Bir şüpheliyi yakalarken birçok kişiden DNA örneği almak gerekir. Ancak suçlu hariç diğer tüm insanların DNA’sının gizlilik nedeniyle sistemden kaybolması gerekir. Bu noktada sıfır bilgi ispatlarından yararlanıp DNA’nın sadece eşleşip eşleşmediğine dair bilgi almak mümkün oluyor.
Kısacası sıfır bilgi ispatları yeni bir alan olmasına rağmen günlük hayatın içine entegre olmuş bir kavram. Bu nedenle ileride ondan daha çok söz edeceğiz gibi duruyor.
Kaynaklar ve İleri Okumalar
- The crazy mathematical concept that underlies all your online security: zero knowledge proofs ; Bağlantı: The crazy mathematical concept that underlies all your online security: zero knowledge proofs (zmescience.com) ; Yayınlanma tarihi: 18 Nisan 2024
- Zero-knowledge proofs explained in 3 examples ; Bağlantı: Zero-knowledge proofs explained in 3 examples (circularise.com) ; Yayınlanma tarihi: 21 Aralık 2022
- What are zero-knowledge proofs? ; Bağlantı: Zero-knowledge proofs | ethereum.org ; Yayınlanma tarihi: 23 Nisan 2024
- S. Goldwasser et al. The Knowledge Complexity of Interactive Proof Systems ; Bağlantı: The_Knowledge_Complexity_Of_Interactive_Proof_Systems.pdf (mit.edu)
Matematiksel








