Finans piyasaları karmaşıktır ve fiyatlar sürekli olarak değişir. Yatırımcılar, bu dalgalanmalar karşısında risklerini yönetmek ve kazançlarını en üst düzeye çıkarmak için matematiksel modeller geliştirirler. Black-Scholes denklemi, bu modellerin en ünlülerinden biridir ve opsiyon fiyatlamasında devrim yaratan bir yaklaşım sunar.

Finansal türev araçlarının fiyatlandırılmasını sağlayan bu denklem, Fischer Black, Myron Scholes ve Robert Merton tarafından geliştirilmiş ve 1997’de Scholes ve Merton’a Nobel Ekonomi Ödülü kazandırmıştır. Black-Scholes modeli, opsiyon fiyatlarını belirlemenin yanı sıra, risk yönetimi ve portföy optimizasyonu gibi birçok finansal analizde kullanılır.
Opsiyon Nedir ve Neden Önemlidir?
İş dünyasında şirketler, mümkün olduğunca risklerini azaltmak isterler. Bunu yapmanın en önemli yollarından biri türev ürünler olarak adlandırılan finansal araçları kullanmaktır. Bu ürünler, sigorta poliçeleri gibidir. Bir şirket bugünden bu türev ürünlerden birini satın alırsa, gelecekte belirli risklere maruz kalmaktan korunmuş olur.
Türev ürünler yalnızca risk yönetimi için değil, bağımsız olarak alınıp satılan yatırım araçları olarak da kullanılmaktadır. Ancak bu ticaret, büyük miktarlarda para kazanmanın yanı sıra kaybetme potansiyeline de sahiptir.

Bir havayolu şirketinin bir yıl sonrası için bir uçuş bileti sattığını düşünelim. Havayolları için en büyük maliyetlerden biri yakıt olduğu için, şirket bilet satışından elde ettiği gelirin bir yıl içinde yükselen yakıt fiyatlarını karşılayamayacağı bir durumla karşılaşmak istemez. Bu riski azaltmak için havayolu şirketi forward sözleşmesi adı verilen bir türev ürün kullanabilir.
Bu sözleşme, şirketin bir yıl sonra yakıtı belirli bir fiyattan satın almasını garanti eder. Ancak burada bir risk de vardır. Eğer yakıt fiyatları düşerse, forward sözleşmesi ile belirlenen fiyat piyasadaki fiyattan daha yüksek olur. Yani şirket gereğinden fazla ödeme yapar.
Bu nedenle, türev ürünleri satan finans kuruluşlarının, bu ürünlerin doğru fiyatını belirleyebilmesi gerekir. İşte burada matematiksel modellemeler ve finans mühendisliği devreye girer. Bu tür türev ürünlerden biri de opsiyonlardır.
Bir yatırımcının, belirli bir varlığı (örneğin bir hisse senedini) belli bir tarihte ve belli bir fiyattan satın alma veya satma hakkına sahip olduğu finansal araçlara opsiyon denir. Opsiyonların fiyatları, piyasa oynaklığı, zaman, faiz oranları ve dayanak varlığın fiyatına bağlı olarak değişir. İşte burada Black-Scholes denklemi devreye girer.
Black Scholes Denklemi Nedir?

1973 yılında Fischer Black, Robert Merton ve Myron Scholes tarafından geliştirilen Black-Scholes modeli, opsiyon sözleşmelerinin teorik değerini hesaplamak için kullanılan ilk yaygın matematiksel yöntemdir. Denklem ilk olarak, Black ve Scholes’un 1973 yılında yayınladıkları bir makalede tanıtılmıştır. Robert C. Merton ise bu makalenin düzenlenmesine katkıda bulunmuş, modelin matematiksel altyapısını genişletmiş ve “Black-Scholes opsiyon fiyatlandırma teorisi” terimini ortaya atmıştır.
Black-Scholes denklemi, opsiyonun önerilen fiyatını dört temel değişkenle ilişkilendirir.
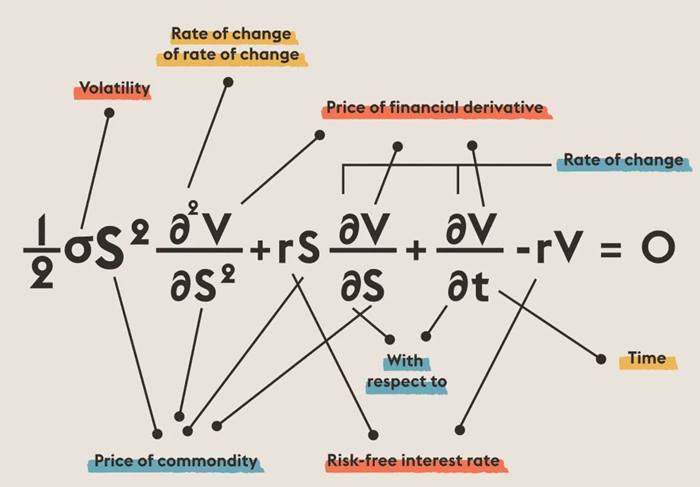
- Zaman (t): Opsiyonun vadesine kalan süre.
- Dayanak varlığın fiyatı (S): Opsiyonun bağlı olduğu varlığın (örneğin bir hisse senedi) güncel piyasa fiyatı.
- Risksiz faiz oranı (r): Genellikle devlet tahvilleri gibi güvenli yatırım araçlarının getirisi olarak kabul edilmektedir.
Dördüncü değişken ise varlığın oynaklığı (σ), yani fiyat değişimlerinin ne kadar dalgalandığını gösteren ölçüttür. Oynaklık, bir varlığın piyasa değerinin ne kadar düzensiz değiştiğini ifade eder.
Black Scholes Modeli Nasıl Ortaya Çıktı?
Pek çok finansal modelin kökeni, Louis Bachelier’in 1900 yılında ortaya attığı fikre dayanır. Günümüzde opsiyonları anlayabilsek de Louis Bachelier’in zamanında gördüğü şey bir kaostu. Bu kaos özellikle de hisse senedi opsiyonlarının fiyatı söz konusu olduğunda ortaya çıkıyordu. Çünkü kimse fiyatlandırmanın tam bir yolunu bulamamıştı.

Bachelier gelecekteki fiyat hareketlerinin geçmiş fiyatlara dayanarak tahmin edilemeyeceğini fark etmişti. Yapılacak en iyi şey herhangi bir zamanda hisse senedi fiyatının düşme ihtimalinin de artması kadar olası olduğunu ve bu nedenle uzun vadede hisse senedi fiyatlarının rastgele bir yürüyüş izlediğini varsaymaktı.
Fiyat hareketlerinin rastgeleliğini göstermek için Bachelier, akışkanlarda gözlemlenen fiziksel bir olay olan Brown hareketi kavramını ödünç aldı. Bir hisse senedi fiyatının rastgele bir yürüyüşe geçmesi durumunda, belirli bir süre sonra herhangi bir değeri alma olasılığının, normal dağılım veya çan eğrisi olarak bilinen bir eğri tarafından verildiğini buldu.
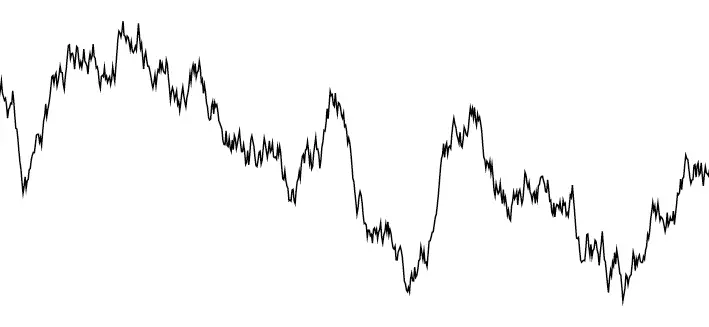
Black-Scholes modeli, Bachelier’in borsa hareketlerini modelleme fikrini hayata geçirmiştir. Ancak Black-Scholes denklemi, doğrudan opsiyonun fiyatını vermez. Bu denklem, opsiyon fiyatının zaman içindeki değişim oranını, diğer değişkenlerin değişim oranlarına bağlı olarak tanımlar.
Black-Scholes modelinin erken dönemdeki başarısı, finans sektöründe farklı finansal enstrümanlar için benzer denklemler geliştirilmesini teşvik etti. Geleneksel bankalar, bu matematiksel modelleri kullanarak kredileri ve işlemleri analiz etti, potansiyel kârları tahmin etti ve riskleri hesapladı.
Ancak daha spekülatif yatırımcılar ve kuruluşlar, bu modelleri daha riskli yatırımlar yapmak için de kullanmaya başladı. Kısa sürede bankalar da bu spekülatif işlemlere yönelerek daha yüksek riskli finansal faaliyetlere girdi.
Black-Scholes Modelinin Sınırlamaları ve Gerçek Piyasalardaki Sorunlar
Her matematiksel model, gerçek dünyayı basitleştirilmiş varsayımlar üzerine inşa eder. Black-Scholes denklemi de fiyat hareketlerinin belirli sabit varsayımlara göre belirlendiğini kabul eder. Ancak, bu varsayımlar gerçek piyasalarda çoğu zaman geçerli değildir. Bu modelin dayandığı başlıca varsayımlar şunlardır:
- Piyasa oynaklığı (volatilite) ve fiyat değişim trendi (drift) sabittir. (Gerçekte, piyasa koşulları değiştikçe volatilite de değişir.)
- İşlem maliyetleri yoktur. (Gerçekte, alım-satım işlemleri için komisyon ve diğer maliyetler vardır.)
- Short-selling (açığa satış) sınırsızdır. (Gerçekte, açığa satışa yasal ve finansal kısıtlamalar getirilebilir.)
- Borç alma ve verme her zaman sabit bir risksiz faiz oranı ile mümkündür. (Gerçekte, faiz oranları piyasa koşullarına bağlı olarak değişir.)
Gerçek finansal piyasalarda bu varsayımların çoğu doğru olmadığı için, Black-Scholes modeli her zaman gerçeğe birebir uymayacaktır.. Ancak, bu model hala modern finansın en önemli araçlarından biri olarak kabul edillmektedir. Bu nedenle de opsiyon fiyatlandırmanın temel çerçevesini oluşturmaya devam eder.
Kaynaklar ve ileri okumalar:
- The mathematical equation that caused the banks to crash. Yayınlanma tarihi: 12 Şubat 2012. Kaynak site: Guardian. Bağlantı: The mathematical equation that caused the banks to crash
- A risky business: how to price derivatives. yayınlanma tarihi: 1 Kasım 2018; Bağlantı: https://plus.maths.org/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi artırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak, bilimin bütünsel yapısı itibarıyla diğer bilim dallarıyla ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı, sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak, ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca, yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım
Matematiksel





