Tüm arkadaşlarınızın bir listesini yapın. Ardından tüm arkadaşlarınızdan aynı şeyi yapmalarını isteyin. Muhtemelen, arkadaşlarınızın listeleri sizinkinden daha uzun olacaktır. “Arkadaşlık paradoksu” olarak bilinen bir fenomene göre, arkadaşlarınız ortalama olarak sizden daha popülerdir.
Hepimizin çok arkadaşı olan biriyle arkadaş olma olasılığımız, az arkadaşı olan biriyle arkadaş olmamızdan daha fazladır. Aynı zamanda Twitter’da takip ettiğiniz kişilerin sizden daha fazla takipçisi olması ve Facebook’taki arkadaşlarınızın çoğunun sizden daha fazla arkadaşı olması ihtimali de daha yüksektir.

Mantığa aykırı geldiğinin farkındayız. Sonucunda ben senin arkadaşın ve sen benim arkadaşımsan, o zaman her birimizin bir arkadaşı olur diye düşünebilirsiniz. Ancak arkadaşlık bu şekilde dengeli gibi görünse de aslında değildir. Paradoksun nedeni, arkadaş ağlarının yapısı ile ilgilidir.
Arkadaşlık Paradoksu Nedir?
Sosyolog Scott Feld, “arkadaşlık paradoksu” fikrini ilk kez 1991’de ” “Why Your Friends Have More Friends Than You Do? (Arkadaşlarınızın Neden Sizden Daha Çok Arkadaşı Var?)” başlıklı bir dergi makalesinde açıkladı. Basit bir hesaplamaya dayanan genel fikir, bir kişinin arkadaşlarının arkadaş sayısının ortalama olarak o kişinin arkadaş sayısından daha fazla olduğudur.

İlerleyen süreçte de matematikçiler, arkadaşlık paradoksunu ortalamaların ötesine taşıyan bir teori buldular. Bu varsayımı açıklayan denklemleri, gerçek dünya durumları ile daha uyumluydu. Araştırmacılar ayrıca, arkadaşlık paradoksundan yola çıkarak “genelleştirilmiş arkadaşlık paradoksu” adlı yeni bir matematiksel teori geliştirdiler. Bu, popüler insanların popüler olmayan insanlardan daha zengin ve yakışıklı olma ihtimalinin daha yüksek olduğunu ileri sürüyordu!
Nedenini anlamak için sadece iki arkadaşı olan bir insanla yüzlerce arkadaşı olan bir insanı karşılaştırın. Şimdi bu iki kişi ile aynı ortama girdiğinizi düşünün. Sonucunda sosyal olarak aktif olan kişi ile arkadaş olma olasılığınız diğer kişiye göre daha fazladır. Ancak aynı durum bu ortamdaki insanların çoğu için de geçerlidir. Tam olarak açıklamak için de bir örneğe göz atalım.
Arkadaşlık Paradoksunu Anlamak İçin Bir Kaç Örnek
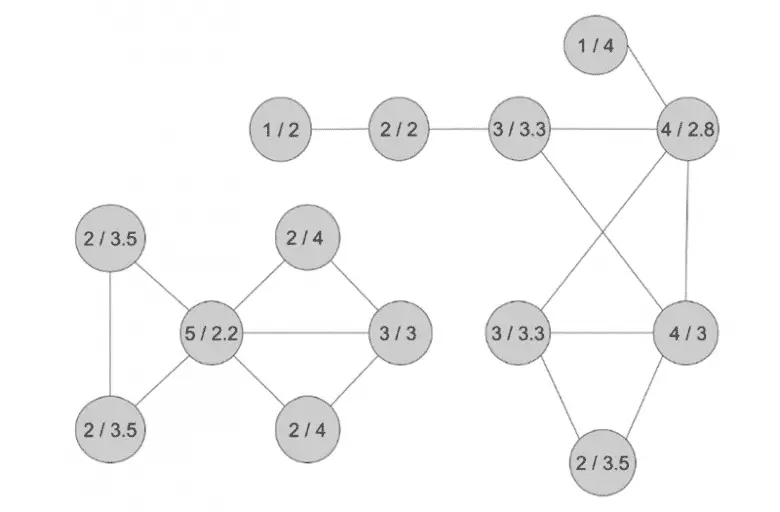
Şimdi yukarıdaki çizimi inceleyelim. Her daire bir sınıfta bulunan kız öğrenciyi temsil etsin. Toplam 14 kızımız var. Daireler arasındaki çizgiler de iki kız öğrencinin birbiri ile arkadaş olduğunu göstersin. Her kız için listelenen ilk sayı, kızın kaç arkadaşı olduğunu göstersin. İkinci sayı da kızın arkadaşlarının sahip olduğu ortalama arkadaş sayısını göstermekte olsun.
Örneğin sol alt köşedeki kızın 2 arkadaşı var. Bu kızın arkadaşlarının arkadaş sayısı ise 3 ve 4. Bu durumda da ortalamaları 3,5. Yani 2 / 3.5 ortalama olarak bu kızımızın arkadaşlarından daha az popüler olduğunu bizlere gösteriyor. Listeyi kontrol ederseniz, bu durumun, 14 kızdan 9’u için geçerli olduğunu göreceksiniz. Sadece 3’ü arkadaşlarından daha popüler ve 2’si arkadaşlarının popülaritesine eşit.
Arkadaşlık paradoksunun anlaşılması kolaydır. En popüler kişiler diğer birçok kişinin arkadaşlık listelerinde görünürken, çok az arkadaşı olan kişiler ise nispeten az sayıda kişinin listesinde görünür. On arkadaşı olan biri, yalnızca beş arkadaşı olan başka bir kişiye göre iki kat daha fazla kişi tarafından arkadaş olarak sayılır.
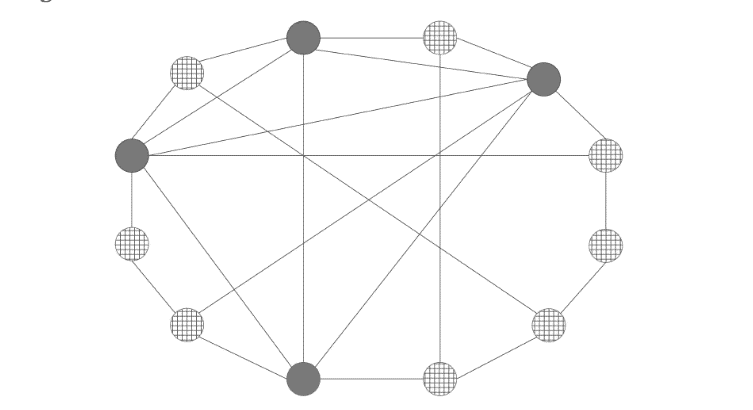
Arkadaşlık paradoksunun sonuçlarını açıkça görmek için basit bir örnek ele alalım. Okulun ilk günü öğrencilerin iki farklı okul forması seçme şansı var: düz veya kareli. Herkes canının istediğini giymiş ve okula gelmiş. Resimde görüldüğü gibi dört öğrenci düz, sekiz öğrenci kareli tercih ediyor. Yani öğrencilerin üçte ikisi kareli tercih ediyor. Bununla birlikte, düz renk tercih eden en popüler dört öğrenci olduğunu unutmayın.
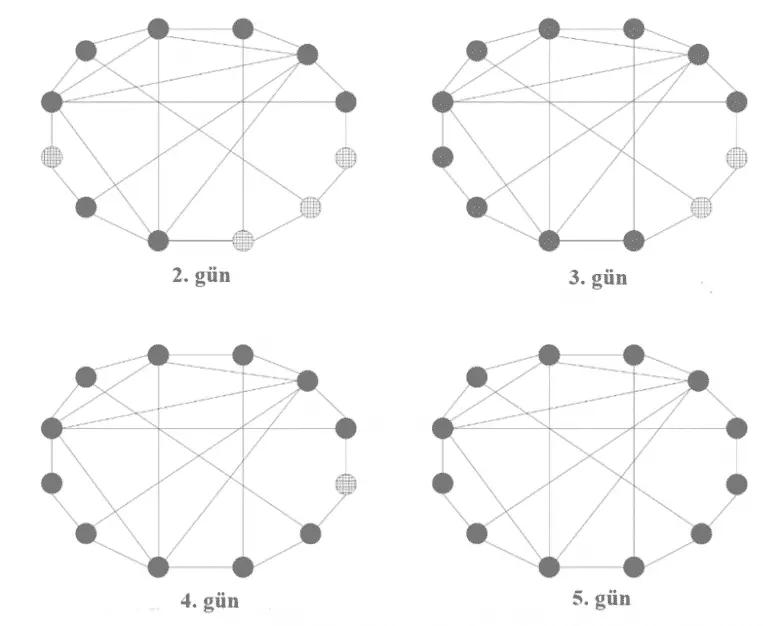
Öğrenciler herkesi aynı anda görmezler sadece arkadaşları ile etkileşimde bulunurlar. Şimdi ilerleyen günlerde neler olabileceğine bakalım. Popüler öğrencilerin hepsi birbirlerini görüyor ve bu yüzden düz renk giymeye devam ediyor. Diğer öğrenciler de çoğunlukla popüler öğrencileri görüyor. Sonra yavaş yavaş tercihlerini değiştirip düz giysiler giymeye başlıyorlar. Beşinci güne gelindiğinde, çoğu kareli tercihiyle başlamış olmasına rağmen, sonunda her öğrenci düz renk giysiler giyiyor.
Arkadaşlık Paradoksunun Düşündürdükleri
Yukarıdaki örnekte fark edebileceğiniz iki husus vardır. Birincisi, en popüler öğrencilerin hepsinin aynı tercihlere sahip olmasıdır. Bu önemli ve popüler kişilerin birbirinin aynısı gibi görünüyor olmasının nedenidir.
İkincisi, popüler öğrencilerin tümünün birbirleriyle arkadaş olmasıdır. Bu güç birliği, davranışlarını güçlendirmekte ve etki alanlarını arttırmaktadır. Bir dahaki sefere sosyal medyaya göz attığınızda ve kendinizi kötü hissettiğinizde, diğer insanların da çoğunun sizinle aynı şekilde hissettiğini unutmayın. Yazının devamında göz atmak isterseniz: Ayşe’den Alya’ya: Popüler Bebek İsimleri Neden Sürekli Değişiyor?
Kaynaklar ve ileri okumalar:
- Jackson, Matthew; The human network : how your social position determines your power, beliefs, and behaviors; Pantheon Books, 2019.
- The friendship paradox: You’ll never be as popular on social media as your friends; Bağlantı: The friendship paradox: You’ll never be as popular on social media as your friends
- The ‘friendship paradox’ doesn’t always explain real friendships, mathematicians say. Yayınlanma tarihi: 11 Haziran 2021; Bağlantı: The ‘friendship paradox’ doesn’t always explain real friendships, mathematicians say.
- George T Cantwell and others, The friendship paradox in real and model networks, Journal of Complex Networks, Volume 9, Issue 2, April 2021, cnab011, https://doi.org/10.1093/comnet/cnab011
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










