Üstel Büyümeyi Anlamamak Riskleri Hafife Almamıza Neden Olur

Üstel büyüme insan beyni tarafından kavranması zor bir kavramdır. Ancak bu zorluk çoğu zaman önemli düşünce hataları yapmamıza da neden olur.

Bir göletin üzerinde bulunan küçük bir nilüfer yaprağının her gün kendisinin iki katı boyuta ulaştığını düşünün. Bu nilüfer 29. günde göletin yarısını kaplamış olsun. Göletin tamamını kapladığı zaman içinde yaşayan tüm canlılar ölecektir. Peki bu canlıların kurtulmak için kaç günü var? Diğer bir deyişle nilüfer hangi gün göletin tamamını kaplar?

Cevap 30. gün olacaktır. Nilüfer neredeyse fark edilmeyecek bir hızla büyümeye başlar. Yirminci gün geldiğinde, göletin yüzde birinin onda biri kadar yer kaplıyordur. Beş gün sonra, yüzde üçe ulaşır. Sonra bir anda, yirmi dokuzuncu günde nilüfer göletin yarısını kaplar. O an geldiğinde ise, herkesi kurtaracak çok az zaman kalmıştır.

Gölet hikayesinden çıkarılacak ders, üstel büyümenin doğasının doğrusal düşünce yapımızla uyumlu olmamasıdır. Ancak yine de üstel büyüme, piramit şemalarından nükleer silahlara, hayatımızın pek çok noktasında karşımıza çıkar.

Bir piramit şemasında, her yeni yatırımcı iki yeni üye daha davet eder, onlar da iki yeni üye daha davet eder. Bu hızlı büyüme, kaçınılmaz olarak yeterli yeni üyenin olmadığı ve sonunda çöktüğü bir duruma yol açar. Piramit yıkıldığında da, çoğu yatırımcı parasını kaybeder. Benzer bir duruma bir nükleer fisyon bombasında da rastlanır.

Önce tek bir uranyum atomu ikiye bölünecektir. Bu bölünme sonucunda hızlı hareket eden nötronları dışarı atar. Nötronlar daha sonra daha fazla atom çekirdeğiyle çarpışır, daha fazla atomu böler. Sonucunda üssel olarak artan bir nükleer zincir reaksiyonu oluşur. 6 Ağustos 1945 sabahı saat 8:15 civarında patlayan ve Japonya’nın Hiroşima şehrini yerle bir eden atom bombası da, üstel büyümenin müthiş gücüdür.

Üstel Büyüme Nedir?

Matematiksel olarak ifade edersek üstel büyümede, belirli herhangi bir anda, bir niceliğin artışı o niceliğin büyüklüğüyle orantılıdır. Dolayısıyla ne kadar büyükse o kadar hızlı artar. Üstel büyüme toplamanın değil çarpmanın gücünden faydalanır. Sonucunda 1,2,3,4,5… biçiminde toplama yardımı ile büyüyen çokluklar, 2,4,8,16,32… biçiminde büyüyenler bir noktadan sonra çok daha yavaş büyüyecektir.

Bir şeyi defalarca ikiye katlamak, üstel büyümeyi anlamanın iyi bir yoludur. Sonuçta sadece 0,1 mm kalınlığında bir kağıt alıp ikiye katlarsanız, yeni kalınlık 0,2 mm olacaktır. Bir biçimde katlamaya devam ederseniz 0,4 ve ardından 0,8 mm kalınlığa ulaşır. Ancak 50 katlamadan sonra kağıdın kalınlığı 100 milyon kilometredir. Bu, yaklaşık olarak Dünya ile Güneş arasındaki mesafe kadardır.

Üstel Büyüme Yanılgısı Nedir?

Üstel büyüme çok yavaş başlayabilir ve bir süre zar zor fark edilebilir. Ancak kaynakların sınırlı olduğu her yerde bunun dramatik sonuçları olacaktır. Sorun şu ki üstel büyüme söz konusu olduğunda doğru çıkarımlarda bulunmamız da her zaman olası değildir. Bunun sonucunda da üstel büyüme yanılgısı adı verilen sorunla kendimizi karşı karşıya buluyoruz.

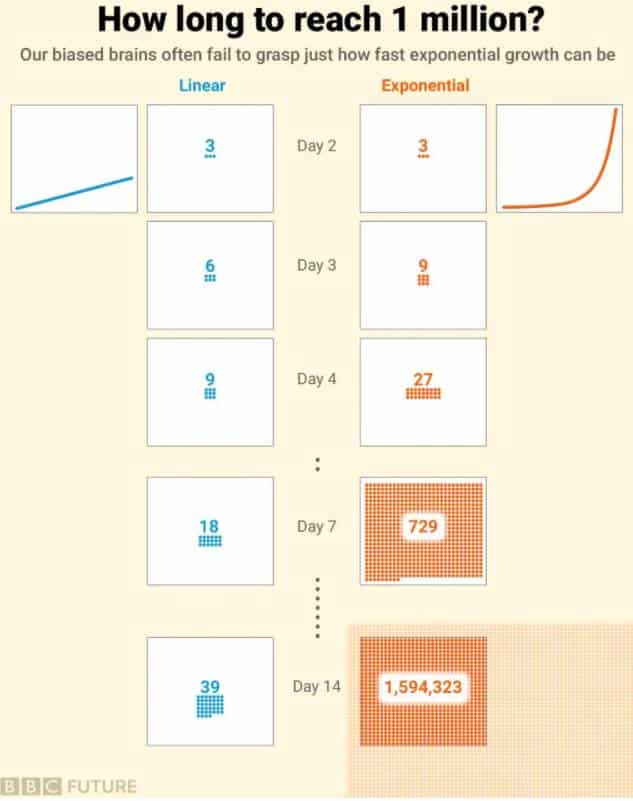
Bankanız ile bir anlaşma yaptığınızı düşünelim. Banka size paranızın her üç günde bir ikiye katlanacağı bir anlaşma teklif etmiş olsun. Bugün sadece 1$ yatırım yaparsanız, dolar milyoneri olmanız kabaca ne kadar sürer? Bir yıl? Altı ay? Kesin cevap, bakiyenizin tam olarak 1.048.576 $ olacağı ilk yatırımınızdan 60 gün sonrasıdır. 30 gün içinde bir milyardan fazla kazanırsınız.

Ve yıl sonuna kadar, 1.000.000.000.000.000.000.000.000.000.000.000.000 dolardan fazlasına sahip olursunuz. Tahminleriniz bu rakama yakın değilse üzülmeyiniz. Yalnız değilsiniz. Pek çok insan, bir değerin ne kadar hızlı arttığını sürekli olarak hafife almaktadır çünkü insan beyni doğrusal büyümeye alışıktır.

Bahçenizdeki ağaç her gün üç elma veriyorsa, iki gün sonra altı, üç gün sonra dokuz elma verir ve böyle devam eder. Üstel büyüme ise aksine, zamanla hızlanır. Bileşik faizin ürkütücü ya da güldürücü yüzü de üstel büyümenin bir sonucudur. Finans dünyasında üstel büyüme en çok, hisse senetleri ve yüksek faizli tasarruf hesapları da dahil olmak üzere çeşitli yatırım araçlarında yaygın olan bileşik faizde görülmektedir.

Sonuç olarak

Üstel büyüme yanılgısının farkına vardıktan sonra değiştirmek mümkündür. Sonuç olarak artış değerleri söz konusu olduğunda, hislerinize güvenmeyin. Yanılgıdan kurtulmak için de, işinize gerçekten yarayacak olan şey bir hesap makinesi ve biraz da matematik olacaktır.

Kaynaklar ve ileri okumalar

• A simple mathematical mistake may explain why many people underestimate the dangers of coronavirus, shunning social distancing, masks and hand-washing.; Yayınlanma tarihi: 13 Ağustos 2020; Bağlantı: https://www.bbc.com
• Schonger M, Sele D. Intuition and exponential growth: bias and the roles of parameterization and complexity. Math Semesterber. 2021;68(2):221-235. doi: 10.1007/s00591-021-00306-7. Epub 2021 Aug 25. PMID: 34795462; PMCID: PMC8386158.

Size Bir Mesajımız Var!

Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel