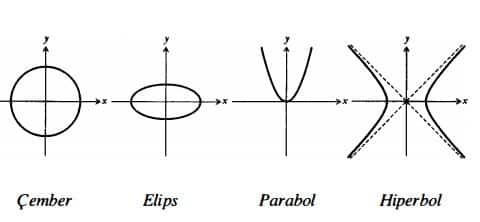
Öğrenim hayatımız sürecinde matematikte çeşitli eğriler ile tanışırız. Bunlardan ilki birinci dereceden denklemler çizilmeleri sonucunda karşımıza çıkan düz çizgilerdir. Sonrasında da ikinci dereceden denklemler ve onların karşılığı olarak da çember, elips, parabol ya da hiperbol gelecektir.

Bu eğrilerin hepsi gerçek dünyada da karşılıklarını kolayca bulurlar. Örneğin, parabol havada uçan bir cismin yörüngesinin biçimidir. Elips, gezegenlerin güneş çevresinde yaptığı harekettir. Güneş saatinin gölgesinin ucunun gün içinde yaptığı hareket ise hiperboldür.
Ancak matematiksel eğriler sadece bu dört şekil ile sınırlı değildir. Gerçek dünyada karşımıza çıkmayan ya da çıksa bile farkı gözlerimiz ile anlayamayacağımız başka eğriler de vardır.
Normal bir elipsin denklemi (x/a)2 + (y/b)2 = 1 biçimindedir. Burada a, elipsin uzun ekseninin uzunluğunun yarısı ve b, elipsin kısa ekseninin uzunluğunun yarısıdır. On dokuzuncu yüzyılda, Fransız matematikçi Gabriel Lamé bu eğriler ile ilgili araştırmalar yaptı. Çok da şaşırtıcı olmayacak biçimde |x/a|n + |y/b|n = 1 biçiminde ortaya koyduğu genelleme günümüzde Lame eğrileri olarak bilinmektedir.
Lame Eğrileri
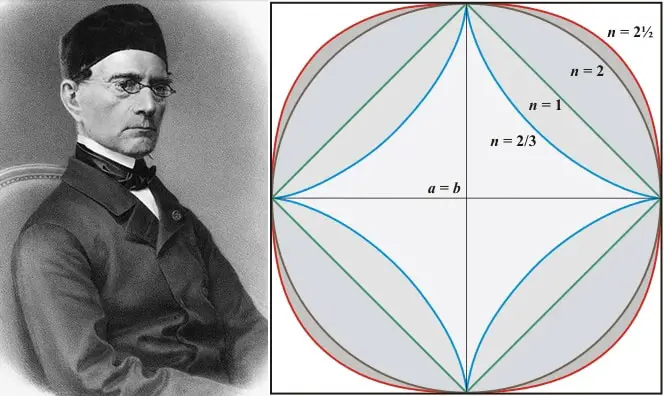
Elips sadece n = 2 olan bir Lamé eğrisidir. n = 2/3 olduğunda ortaya astroid adı verilen dört köşeli bir yıldız şekli çıkar. Ayrıca 2’den büyük tüm n değerleri için ise, Lame eğrileri süper elips olarak bilinmektedir. Bir süper yumurta şekli ise n = 2.5 ve a/b = 6/5 oranlarına sahip olan bir süper elipsin kendi ekseni etrafında döndürülmesi sonucunda ortaya çıkacaktır. Bunlar çok soyut kavramlar gerçek hayatta hiç bir işimize yaramaz demeden önce hemen bir örnek verelim.
Sergels Torg Meydanı Sorunu

Stockholm şehir merkezinde Sergels Torg isimli bir halk meydanı vardır. 1950’lerde Sergels Torg’u tasarlayan şehir planlamacıları geometrik bir problemle karşı karşıya geldiler. Dikdörtgen biçimindeki bir alana yapılacak en iyi yürüyüş yolu biçimi ne olmalıydı?
Cevap arayışı içinde, projede çalışan mimarlar, Danimarka’da yaşayan, bir ressam ve matematikçi olan Piet Hein’a danıştılar. Piet Hein’ın çözümü basit bir biçimde matematiği kullanmak idi. Bunun için elips denklemindeki üs değerini değiştirdi.
Piet Hein, oval ve dik kenarlar arasındaki sanatsal anlamda en iyi uyuşmanın n değerinin 2.5 alındığında meydana geldiğine karar verdi. Sonuç da uygulamaya karar verdiği şekil az evvel de bahsettiğimiz süper elips oldu. Ancak bu garip süper eğrilerin hayatımıza dahil olması bunla da sınırlı değil. Stockholm’ün süper eliptik yürüyüş yolu başka mimarlar tarafından da kopyalandı. Örneğin 1970 ve 1986 yıllarında dünya kupasının oynandığı Mexico City’deki Azteca stadyumu aynı biçimde inşa edildi.
Piet Hein’ın zihni süper elipste durmadı. Ayrıca 1970’lerde Piet Hein, çeşitli formlarda ürettiği süper yumurta biçimde objeleri piyasaya sürdü. Süper yumurtanın beklenmedik özelliklerinden biri düşmeden uçlarının üzerinde durabilmesidir. Merak uyandıran güzel nesnelerdi. Aslında Piet Hein’ın tüm eğrileri zamanla gündelik hayata yayılarak tasarımcıların vazgeçilmezlerinden oldu.

Yeni Bir Süper Eğri: Gömböc
Ancak süper eğrilerin hikayesi burada bitmedi. Sonraki süreç de bir garip süper eğri ile daha tanıştık. Bu şeklimizin adı da Macarca ‘küre’ anlamına gelen için gömböc idi. Gömböc’ün varlığı ilk olarak 1995 yılında Rus matematikçi Vladimir Arnold tarafından tahmin edildi. Bir gömbecin neye benzediğini aşağıda görebilirsiniz. Gömböc’ün gerçek dünyada ve birçok farklı biçimde var olabileceğinin kanıtı ise, 2006’da Macar matematikçi ve mühendis Gábor Domokos ve öğrencisi Péter Várkonyi’den geldi.

Bildiğiniz gibi, kaplumbağalar bir biçimde ters dönerlerse başları belaya girer. Sonucunda tekrar eski hallerini almak bir ölüm kalım meselesidir. Kimi kaplumbağa türleri bunu kolaylıkla başarır. Domokos ve Várkonyi, Budapeşte Hayvanat Bahçesi’nde farklı kaplumbağa türlerinin kabuklarının şekillerini ölçmek ve analiz etmek için bir yıl geçirdiler. Kaplumbağa vücut şekli ve kendi kendini yönetme yeteneği ile ilgili ortaya çıkan açıklamaları, gömböc geometrisini açıklamalarına yardımcı oldu.
Gömböc, bir kararlı ve bir kararsız denge noktasına sahip ilk ve tek üç boyutlu homojen nesne olarak kabul görmektedir. Bu özelliği sayesinde hangi konumda bırakılırsa bırakılsın, bir kaplumbağa gibi, kendi temel konumuna geri dönebilmektedir. Yazının devamında ayrıca göz atmak isterseniz: Yumurta Şeklinin Geometrisini En Sonunda Anlayabildik
Kaynaklar ve ileri okumalar:
- Gabriel Lamé; Bağlantı: https://mathshistory.st-andrews.ac.uk/Biographies/Lame/
- Superellipse; Bağlantı: https://en.wikipedia.org/wiki/Superellipse
- Gömböc; Bağlantı: https://www.atlasobscura.com/places/gomboc
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel