Walt Disney Studios’un bir yan kuruluşu olan Pixar, bilgisayar animasyonunun öncülerinden biri olarak kabul edilmektedir. Finding Nemo (2003), The Incredibles (2004), WALL-E (2008), Inside Out (2015) ve Toy Story 4 (2019) gibi ödüllü uzun metrajlı filmler en çok bilinen çalışmaları arasında yer almaktadır. Daha az bilinen şey, devrim niteliğindeki animasyonlarının altında matematiktir.
Pixar teknolojisi matematik ile bilgisayarın şahane bir kesişimi, hatta kaynaşmasıdır. Animasyon ve matematik ilişkisini bilmek, matematiğin gücünü anlamamız için önemlidir. Başlıkta Ters Yüz adlı animasyon filminden bir kare görüyoruz. Bu kareyi oluşturmak için matematikten nasıl yararlanıldığına bir göz atalım.
Renderleme
Renderleme hayali 3D bir sahnenin 2D olarak oluşturulmasıdır. Gerçekçi bir şekilde yapılmazsa sahnenin hiçbir cazibesi ve inandırıcılığı kalmaz. Renderleme sahneye yerleştirilen bir kamera aracılığıyla yapılmaktadır. Ancak bu kamera da diğer nesneler gibi matematiksel olarak oluşturulmuş hayali (geometrik) bir cisimdir.
Bilgisayara render komutu verildiğinde renderer denen bir yazılım devreye girer. Bunun sonucunda kameranın sahneyi nasıl “göreceğini” hesaplanır ve görüntüyü oluşturur. Oluşturduğu bu görüntüyü ekrana yansıtarak, bizim de görmemizi sağlar.
Bu karmaşık işlemler matematiksel yöntemlerle başarılr. Aşağıdaki görselde “renderleme” denklemi görülmekte. Ekranda beliren her bir nokta, aslında kendisine doğrudan ve dolaylı yollardan gelen ışık ışınlarının bir toplamı, yani integralidir.

Aslında bilgisayar her şeyi bu kadar kesin hesaplamıyor. Çünkü hesaplanması gereken sonsuz sayıda nokta ve sonsuz sayıda yansıma var. Hiçbir bilgisayar bu hesabın altından kalkamaz. Bilgisayarların gerçekte yaptığı istatistik hesap tekniklerini kullanarak render denklemini sadeleştirmekten ibaretir. Aslında bilgisayar grafiklerinde istatistiğin birçok dalı kullanılmaktadır.
İstatistiğin dışında elbette fizik de devreye girer. Işık skalar bir büyüklük olmadığından bilgisayarda ışığı temsil etmek için hangi modeli kullanacağınıza karar vermelisiniz. Işığın kutuplanması (polarizasyonu) dikkate alınacak mı? Ya da 255’ten büyük ışık şiddetlerine izin verilecek mi?
(Bilgisayarlarda genellikle siyah için 0, beyaz için ise 255 değeri kullanılır. Bu da ışığın sadece 256 parlaklık seviyesine izin verildiği anlamına gelir. Oysa gerçek yaşamda ışığın parlaklığının bir üst sınırı yoktur. Bir sahnede Güneş gibi parlak bir cisim varsa 255’ten daha büyük değerlerin kullanılması zorunlu olur.) Kestirme yollar kullanılmadığı takdirde hiçbir bilgisayarın böylesine muazzam bir hesap yükünün altından kalkamayacağı açıktır. O halde işin içine ciddi miktarda mühendislik optimizasyonu girmektedir.
Simülasyon
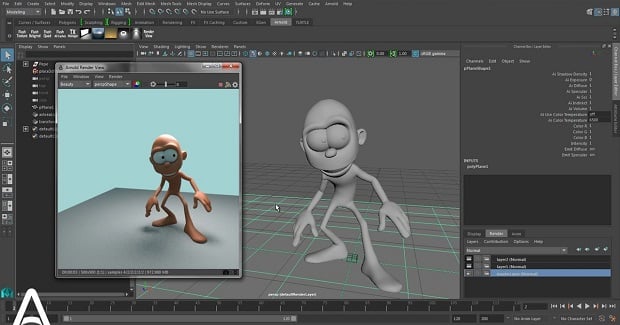
Resmin nasıl çizildiğini anladık, şimdi neyin resmini çizeceğimize karar verme zamanı. Üstteki resimde Üzüntü (filmdeki bir karakter) erimiş lavlar üzerinde yüzüyor, tüylü bir kazak giyiyor ve konuşurken cildi deforme oluyor.
Akışkanların animatörler tarafından canlandırılması çok zordur. Bunun yerine akışkanı simüle etmek daha iyi sonuç verir. Canlandırma sinemasında fiziksel simülasyonların önemi büyüktür. Filmlerde gördüğümüz birçok şey simülasyonla oluşturuluyor. (Saç, kıllar, giysiler, kalabalıklar, kar taneleri, çarpışmalar, ateş, duman vs.)
Örneğin üzüntünü giydiği süveteri ele alalım. Kumaşlar birbirine bağlı minik yaylardan oluşmuş bir sistem şeklinde modellenir. (Her bir kumaş iplikçiği minik bir yay gibi davranır.) Simülasyonun mantığı kısaca budur. Üzüntü hareket ettikçe kumaşın nasıl kıvrılacağı simülasyon yazılımı tarafından hesaplanır. Üzüntü’nün saçı da simüle edilmiştir. Simülasyonda her bir saç teli kafa hareketlerinden etkilenen fiziksel yaylar gibi ele alınmaktadır. Sonuç olarak simülasyon motoru (yazılımı), bütün bunları hesaba katarak her bir saç telinin bir arada nasıl hareket edeceğini hesaplar.
Sahneleme
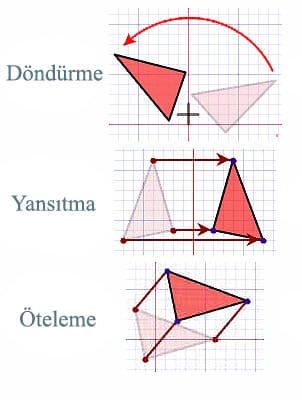
Bir sahnenin 3D olarak temsili matematiğin en temel dallarından biri olan doğrusal cebir sayesinde olmakta. (Bkz. Khan Akademi.) Modelciler sık sık karakterlerin 3D kafesi üzerindeki noktaların yerini değiştirirler. Hem de bunu binlerce kez yapmak zorunda kalırlar. 3D uzayda bir noktayı yerinden oynatmak, yani ona bir dönüşüm uygulamak, doğrusal cebir sayesinde mümkün oluyor.
Döndürme, boyutlandırma ve öteleme gibi temel dönüşümler işin kolay kısmıdır aslında. (Sadece matrislerin toplamı ve çarpımı…) Doğrusal cebir bundan çok daha zor işlerde de kullanılmaktadır. Bir örnek ters kinematik (inverse kinematics) olacaktır.
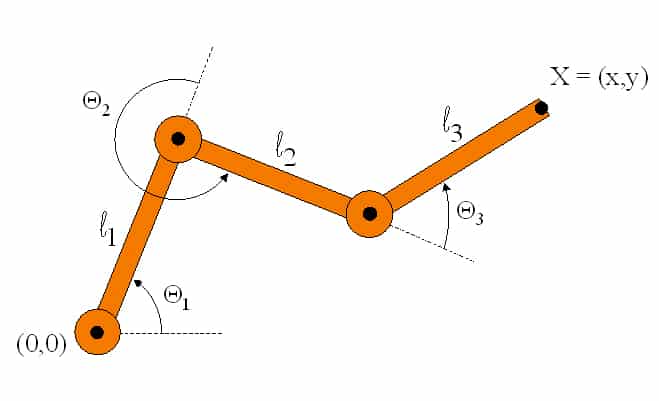
Ters Kinematik, zincir gibi birbirine bağlı nesnelerin (el, ön ve üst kollar, omuz ve gövde) hareketini çözümleyen bir animasyon teknolojisidir. Ters kinematikte siz sadece uçtaki nesneyi (eli) hareket ettirirsiniz, geri kalan nesnelerin hareketi bilgisayar tarafından hesaplanır. Böylece canlandırma sanatçısının işi kolaylaşır.
Bir simülasyonu oluşturan binlerce minik yay, devasa bir denklem sistemi oluşturur. Bu sistemin çözümü doğrusal cebir yardımıyla yapılmaktadır. Simülasyonlar esasında binlerce satır ve sütundan oluşan devasa matrislerle yapılan işlemlerdir.
Üzüntü’nün yanağı sıkıldığında yanağının alacağı şekli de yine doğrusal cebir belirliyor. Bir sıkışma simülasyonunda hacim korunmazsa simülasyon gerçekçi görünmez. (Yanak sıkıldığında etin biçimi değişse de hacim değişmemelidir.)
Son bir örnek de çarpışma simülasyonlarıdır. Çarpışma karmaşık bir dinamik simülasyondur. Çarpışan cisimlerin çarpışma noktaları, çarpışma sırasındaki yön ve hızları hesaba katılmalıdır. Ayrıca çarpışan cisimlerin esnekliği gibi özellikleri de simülasyona dâhil edilmelidir. (Çelik bilyelerin çarpışmaları ile çamur toplarının çarpışmaları birbirinden farklıdır.)
Gölgeleme ve Doku Oluşturma
Gerçek yüzeyler genellikle çok karmaşıktır. Bir ağaç kütüğünü düşünelim. Kütüğün yüzeyindeki damarlar, reçine, nem, böceklerin açtığı yaralar vs. gibi birçok şeyi tek tek modellemek çok zordur. Bunun yerine o yüzey bir doku ile kaplanır. Ancak kaplama doğru biçimde simüle edilemezse, kütük göze çok yapay görünecektir.
Gerçek yüzeyler bilgisayarda yaratılmış olan yüzeylerden çok daha düzensizdir. Bu yüzeylerin geometrilerinin bilgisayarda birebir oluşturulması pratik olmaz, çünkü milyarlarca minik üçgen kullanmak gerekir. Bunun yerine gölgeleme teknikleri (Shading) kullanılarak yüzeylerin gerçekçi görünmesi sağlanır. Gerçi shading kelimesini biz gölgeleme olarak çevirdik ama doku oluşturma ya da doku kaplama demek daha doğru olacaktır.
Burada makine öğrenmesi, doğrusal regresyon analizi ve çeşitli parametrik modeller devreye girmektedir. Bunun yanında BSSDF modelleri de aktif olarak araştırılmaktadır. Aslında makine öğrenmesi ile yüzey dokularının nasıl görüneceğini tahmin etmek mümkündür. Yani, ışınların izleyeceği yolları tamamen hesaplamaya gerek kalmadan, tahminle aynı sonuçlara ulaşmak mümkün.
Bu sonuçlar istatistik dağılımlardan faydalanarak da elde edilmektedir. Bu yolla örneğin süveter, saç ya da deri gibi pürüzlü yüzeylerin kendine özgü parıltısı oluşturulmaktadır.
Animasyonlarda Kullanılmakta Olan Diğer Matematik Dalları
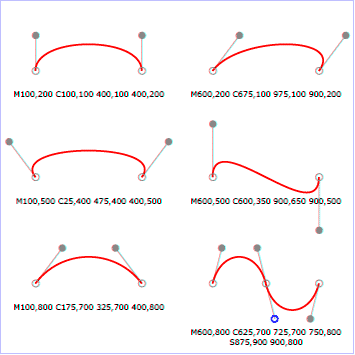
Paraboller, parametrik eğriler, fraktallar bilgisayar grafiklerinde her zaman karşımıza çıkıyorlar. Parametrik eğrileri ele alalım. Bunlar nod denen 3D noktaları birbirine bağlayan eğri parçalarını tanımlayan denklemler kümesidir. Bir çimen yaprağının biçimi parametrik eğrilerle oluşturulmaktadır. Bir topun zıplamasını tanımlayan hız-zaman grafiğinde de aynı eğriler karşımıza çıkar. Canlandırmacı, bu eğrilerle oynayarak animasyonun daha gerçekçi olmasını sağlar. Bütün bunlar Bezier splines denen parametrik eğriler sayesinde olmaktadır.
Sinyal İşleme
Ters Yüz filminin karakterleri parıltılı bir hâleye sahipler. Bu da kenarlarında tırtıklı bir görüntü oluşmasına neden oluyor. Bu tırtıklar bilgisayar grafiklerinde çok ciddi bir sorundur. Yakından bakıldığında bilgisayar ekranındaki şekillerin minik karelerden (piksel) oluştuğu görülür.
Düzgünleştirme algoritmaları uygulanmazsa çizgiler göze düzmüş gibi görünmez. Özellikle kenar ve konturlarda merdivensi bir görünüm oluştururlar. Bu istenmeyen görüntüye aliasing denir. Aliasing ciddi bir sorundur.
Bilgisayar bilimcileri bu pürtüklü görüntüyü ortadan kaldırmak için anti-aliasing yani düzgünleştirme algoritmaları kullanırlar. Düzgünleştirme algoritmaları, çizgilerin testere ağzı gibi görünmesini engeller. Anti-aliasing algoritmaları sayesinde ekranındaki harflerin kenarları düzgün görebiliyoruz.
Bilgisayar grafiklerinde kullanılan matematiğe öğrenmek için Khan Akademi’nin Pixar-in-a-Box iyi bir başlama yeridir. Ayrıca kaynaklar kısmındaki yazılara da göz atarak matematik ve animasyon ilişkisi hakkında daha fazla fikir edinmeniz mümkündür. Ayrıca göz atmak isterseniz: Neden Çizgi Film Karakterlerinin Genelde Dört Parmağı Vardır?
Kaynaklar ve ileri okumalar:
- What type of mathematics is behind Pixar animation?; Bağlantı: https://www.quora.com/
- Alp AKKAYA; Güncel animasyon teknolojilerinin film jeneriklerine etkisi; Bağlantı: https://acikbilim.yok.gov.tr
Matematiksel