1969’da İngiliz matematikçi John Conway, karmaşık davranışlar yaratmak için baştan çıkarıcı derecede basit bir kurallar dizisi tasarladı. “The Game Of Life” yani “Hayat Oyunu”, basit kurallarla başlayan ve karmaşık yapılar üreten bir simülasyon oyunudur.

Hayatla ilgili şaşırtıcı şeylerden biri, onun katıksız karmaşıklığıdır. Bir grup hücre bir araya gelerek insan beyni kadar karmaşık veya bir kelebeğin kanadındaki desenler kadar narin, güzel ve son derece organize bir şeyi nasıl oluşturabilir? İlgili süreçleri tanımlama ve canlı organizmaları anlamamızı geliştirme umudu var mı?
Şimdiye kadar kimse hayatın sırrını tamamen çözemedi, ancak matematik bu konuda bize bazı ilginç iç görüler veriyor. Bunlardan biri, karmaşıklığın bazı çok basit kurallardan kaynaklanabilmesidir. Bunun bir örneğine, 1970 yılında matematikçi John Conway tarafından icat edilen The Game Of life yani Hayat Oyununda rastlanır.

Bu oyun aslında bildiğimiz oyunlara fazla benzemez. İki değil tek bir oyuncu vardır. Tek yapmanız gereken sahneyi ayarlamak ve oyunun gelişmesini izlemektir. Oyun bir dama tahtası benzeri ızgara üzerinde oynanır. Başlangıçta, bazı kareler bir organizma içerir ve bazıları ise içermez. Her karenin bir üstte, bir altta, bir solda, bir sağda ve dört köşede olmak üzere sekiz komşusu vardır. Bir sonraki adımda, yeni organizmalar aşağıdaki basit kurallara göre doğar, ölür veya hayatta kalır.
Conway’in Hayat Oyunu Kuralları
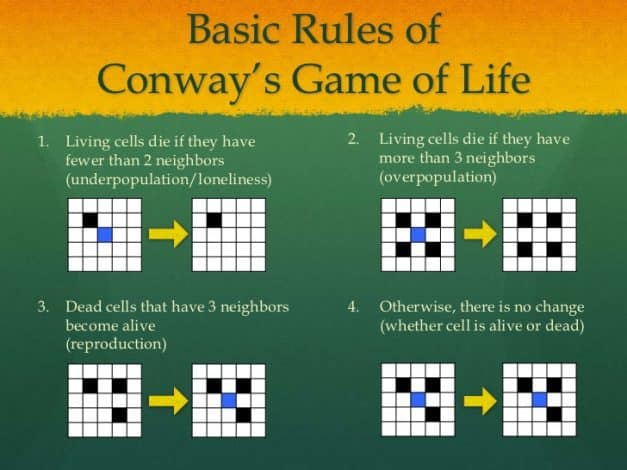
- Sekiz komşu karesi yalnızca bir başka organizma içeren veya hiç içermeyen her organizma yalnızlıktan ölür. Bir sonraki adımda kaybolur.
- Dört veya daha fazla komşu organizmaya sahip her organizma aşırı nüfustan dolayı yok olur.
- İki veya üç komşu organizmaya sahip her organizma hayatta kalır.
- Tam olarak üç kareye bitişik olan her boş kare ise bir doğum karesidir. Bir sonraki hamlede içinde yeni bir organizma belirecektir.
Gördüğünüz gibi kurallar aslında son derece basittir. Ancak buna rağmen, gelişen hücre kalıplarından inanılmaz derecede karmaşık davranışlar ortaya çıkar. Bu basit kurallar, ızgaranın olası birçok farklı başlangıç konfigürasyonundan gelişen şaşırtıcı derecede çeşitli desenler veya “yaşam formları” dizisi yaratır.
Oyunun ismine rağmen, John Conway adını verdiği sistemi geliştirdiğinde, hayatı simüle etmeyi aslında hiç amaçlamıyordu. Yine de oyunun gerçekçi doğası devamında dünyanın her yerinde hayal gücünü ele geçirdi. Conway’in asıl amacı tamamen matematikseldi – sözde evrensel bir sistem, yani keyfi hesaplamalar yapabilen bir sistem – bir tür sonsuz programlanabilir bilgisayar bulmaya çalışıyordu.
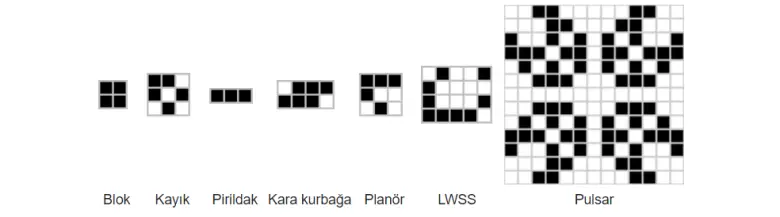
Matematiksel olarak bu oyun aslında 0 (sıfır) oyunculu bir oyun. Oyunun akıbetini belirleyen tek koşul başlangıçtaki canlı-ölü hücrelerin dağılımı. Ve herhangi bir başlangıç düzeninin sonunun neye varacağını tahmin etmek imkansız. Yani matematiksel olarak başlangıç koşuluna göre sistemin nasıl ilerleyeceğini sabitleyen algoritmik bir yapısı yoktur.
Conway’in Hayat Oyunu Bir Oyundan Çok Daha Fazlası Oldu
Conway’in dikkat çekici oyunu, ilk olarak, Scientific American’ın Ekim 1970 sayısında Martin Gardner’ın “Matematiksel Oyunlar” sütunu aracılığıyla dünyanın dikkatine sunuldu. Conway başlangıçta seçilen hiçbir kalıbın sonsuza kadar büyümeyeceğini düşünüyordu. Ona göre oluşan tüm desenler eninde sonunda bir miktar kararlı hale gelecekti. Bu noktadan sonra da ya yok olacak ya da salınım durumuna geçecekti.
Gardner’ın oyunla ilgili 1970 tarihli makalesinde Conway, bu varsayımı kanıtlayacak veya çürütecek ilk kişi için elli dolarlık bir ödül ortaya koydu. Haftalar içinde ödül, matematikçi ve programcı Bill Gosper tarafından talep edildi. Ödülü elde etmenin bir yolu da kalıpları keşfetmekti. O da bunu yaptı.

Hayat Oyununun en önemli katkısı hücresel otomatların kullanımını teşvik etmesi oldu. O zamandan beri hücresel otomatlar fizik, bilgisayar teknolojileri ve matematik dünyasında yaygın biçimde kullanılıyor. Ayrıca Conway’in Yaşam Oyunu “Turing complete”tir yani herhangi bir Turing makinesi modellenebilir. Yani Hayat Oyunu ile bir bilgisayar yapılabilir.
Oyun ayrıca yeni yaşam formlarını bulma umuduyla kalıplar inşa eden programcılardan oluşan bir “Lifenthusiast” kültü oluşturdu. ( Terim, özellikle yeni ve ilginç kalıplar keşfetmek gibi oyuna katkıda bulunan kişilere atıfta bulunmak için kullanılır.)
Hayat oyunu ayrıca bir software endüstrisi geliştirdi. Konu hakkında binlerce kitabın basılmasına da sebep oldu. İnternet ortamında da bu oyunu deneyimleyebileceğiniz kolay kullanımlı uygulamalar mevcut. Hayat oyunu hakkında daha fazla bilgiyi oyunun yaratıcısı Conway’in ağzından daha fazla öğrenebilirsiniz.
Kaynaklar ve ileri okumalar:
- Maths in a minute: Cellular automata ;Yayınlanma tarihi: 16 Mayıs 2017. Kaynak site: Plus Math Bağlantı: Maths in a minute: Cellular automata/
- Games, Life and the Game of Life; Yayınlanma tarihi: Kaynak site: Plus Math. Bağlantı: Games, Life and the Game of Life/
- Math’s ‘Game of Life’ Reveals Long-Sought Repeating Patterns. Yayınlanma tarihi: 18 Ocak 2024. Kaynak site: Quanta Magazine. Bağlantı: Math’s ‘Game of Life’ Reveals Long-Sought Repeating Patterns
Size Bir Mesajımız Var!
Matematiksel, matematik ile ilgili önyargıları yıkmak amacını taşıyan bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










