Bu makalede ne kadar bilgi var? Söylemesi zor. Sonuçta uzunluğu içindeki bilginin bir göstergesi değil. Peki içindeki bilginin az ya da çok olup olmadığını anlamak için kullanabileceğimiz bir araç var mı? Matematikçiler bu soruya evet cevabını verdiler. Sonucunda da karşımıza Kolmogorov Karmaşıklığı adıyla da bilinen Algoritmik Bilgi Teorisi çıktı.

1960’ların başında, Gregory Chaitin adında Amerikalı bir genç, dünyaca ünlü Rus matematikçi Andrey Kolmogorov ve bilgisayar bilimi öncüsü Ray Solomonoff, bağımsız olarak karakter dizilerinin karmaşıklığını ölçmenin bir yolunu formüle ettiler. Fikirleri Kolmogorov Karmaşıklık Teorisi veya Algoritmik Bilgi Teorisi olarak anılmaya başlandı.
Bunu yapmak için bilgiyi makinelerin yaptığı biçimde ele aldılar. Sonucunda bir makine için bir bilgi yalnızca bir dizi sembolden oluşacaktır. Bu sembol yığının uzunluğu bilginin doğası hakkında bize bir fikir sunabilir. Dizedeki bilgiler sıkıştırılabiliyorsa, bunu yapan kısa bir program olmalıdır. Eğer başaramazsa program daha uzun olacaktır.
Bununla ne demek istediğimizi daha iyi açıklamak için basit bir örnek üzerinden ilerleyelim. Bir dizinin yüz tane sıfırdan oluştuğunu hayal edin. Bu dizinin çıktısını alan bir programın yalnızca “0 yazdır; 100 kez tekrarla” gibi bir şey söylemesi gerekir. Farklı programlama dilleri bunu yapmak için farklı komutlar kullansa da genel fikir aynı olacaktır.
(Örneğin, 2 + 2 eklemek için bir komut dosyası, bir metin-konuşma programından daha düşük Kolmogorov karmaşıklığına sahiptir.)
Yani bu oldukça basit bir dizi için kısa bir program yeterlidir. Öte yandan, dizginiz herhangi bir desen olmaksızın 0’lar ve 1’ler içeriyorsa, bunu yapmanız olası olmayacaktır. Programınızın print komutundan sonra dizenin tamamını alıntılaması gerekir. Bu da programın dizinin kendisinden biraz daha uzun olacağı anlamına gelir.
Kolmogorov Karmaşıklığı Nedir?
Belirli bir diziyi üreten ve sonra duran (sonsuz döngüler istemiyoruz) en kısa bilgisayar programının uzunluğuna, bu fikri ortaya atan üç kişiden biri olan Andrey Kolmogorov‘e ithafen dizinin Kolmogorov karmaşıklığı denir. Eğer karmaşıklığı yapı eksikliği olarak yorumlarsanız, o zaman isim daha anlamlı olur.
Kolmogorov karmaşıklığı bilginin iletimi, sıkıştırılması ve tanımlanmasının inceleyen bilgi teorisi kapsamında incelenir. Alan, mühendislik, matematik ve bilgisayar bilimlerindeki uygulamalarla multidisiplinerdir. Algoritmik bilgi teorisi, bilgi teorisinin bilgisayar bilimi ile ilgili alt alanıdır. ( Bilgi teorisi ile ilgili detaylar için bu yazıya göz atınız: Bilgi Teorisi Nedir? Bilgi Matematiksel Olarak Nasıl Ölçülebilir?)
Şimdi aşağıdaki üç diziyi inceleyelim.
- 100100100100100100100100100100100100100100100100100100100100100100100
- 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
- 38386274868783254735796801834682918987459817087106701409581980418.
Bu dizeleri nasıl tanımlayabiliriz? Bunların ilk ikisini kısaca tanımlayabileceğimiz açıktır. Birincisi basitçe tekrar tekrar “100” kalıbıdır. İkincisi ise ilk birkaç asal sayının listesidir. Peki üçüncüsü ne olacak? Bunu daha iyi ve daha kısa bir biçimde açıklamak mümkün mü? Yukarıdaki üç diziye bakalım. İlk iki dizi nispeten kısa bilgisayar programları ile tanımlanabilir:
- 100’ü 30 kez yazdır.
- İlk 25 asal sayıyı yazdır bu program konutları olabilir.
Birinci programın Kolmogorov karmaşıklığı ikinci programın Kolmogorov karmaşıklığından daha azdır çünkü ilk program ikinci programdan daha kısadır. Ancak üçüncüsünde ise belirgin bir model yoktur. Bu dizeyi üretmek için uzun bir program gerekir, bu durumda dize karmaşıktır ve daha fazla algoritmik içeriğe sahiptir.
Kolmogorov Karmaşıklığı Nerede Karşımıza Çıkar?
Bir dizinin Kolmogorov karmaşıklığını, bu dizideki bit cinsinden ölçülen “bilgi miktarı” olarak yorumlamak bizi bazı pratik sonuçlara götürür. Dosya sıkıştırma, tahmin edilebileceği gibi, Kolmogorov karmaşıklığının ana uygulama alanlarından biridir.
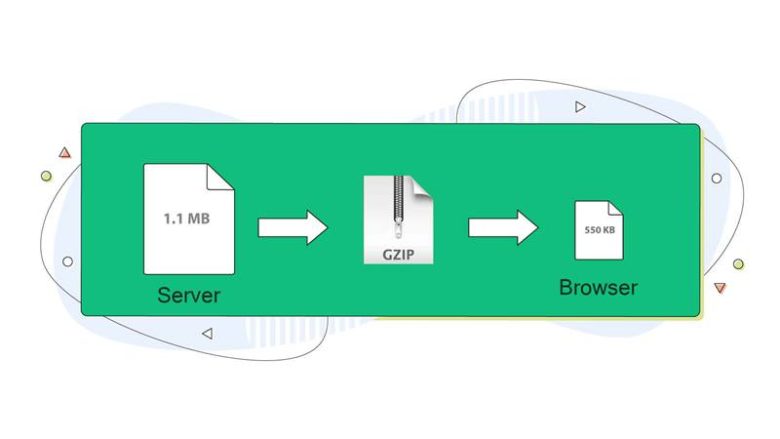
Bildiğiniz gibi, zip, gzip, bzip2, sıkıştırma, rar, arj, vb. gibi programlar, bir dosyayı (metin, resim veya diğer bazı veriler) muhtemelen daha kısa bir dosya biçiminde sıkıştırır. Orijinal dosya daha sonra bir “açma” programı ile geri yüklenir. Düzenli bir yapıya sahip bir dosya önemli ölçüde sıkıştırılacaktır. Öte yandan, düzenliliği olmayan bir dosya pek sıkıştırılamaz ve sonucunda sıkıştırılmış boyutu orijinal boyutuna yakındır.
İki tür sıkıştırma algoritması vardır: kayıpsız ve kayıplı sıkıştırma. Kayıpsız sıkıştırma algoritmaları, bir veri parçasının herhangi bir bilgi kaybı olmadan sıkıştırılmasına ve ardından sıkıştırılmasının açılmasına olanak tanırken, kayıplı algoritmalar sıkıştırma sırasında bilgi kaybına neden olur. Kolmogorov karmaşıklığı, kayıpsız sıkıştırma algoritmalarının sınırlarını etkili bir şekilde tanımlayarak, performanslarının değerlendirilmesinde kullanılır.
Herhangi bir dizinin Kolmogorov karmaşıklığını basit bir şekilde hesaplayabilecek bir bilgisayar olsaydı harika olurdu. Ne yazık ki böyle bir bilgisayar var olamaz! Modern bilgisayarlar ne kadar güçlü olsa da bu görev gerçekleştirilemez. Bir bilgisayar belirli bir kalıbın çıktısını veren kısa bir program bulabilir ancak daha da kısa bir program da mevcut olabilir. Asla bilemeyeceğiz. Bu nedenle de Kolmogorov karmaşıklığının hesaplanabilir olmamasından bahsedilir.
Sonuç Olarak;
Bazı kısıtlamaları olsa da Kolmogorov karmaşıklığı, matematik ve bilgisayar bilimlerinin tamamında, özellikle de istatistik ve hesaplama karmaşıklığı alanlarında geniş kapsamlı çıkarımlara sahip, inanılmaz derecede faydalı bir fikirdir. Konuya giriş anlamında yazdığımız bu makale ilginizi çekti ise daha fazla araştırma yapmanız önerilmektedir.
Kaynaklar ve ileri okumalar
- Information is complexity; Yayınlanma tarihi: 24 Mart 2015. Kaynak site: Plus Maths. Bağlantı: https://plus.maths.org
- Li, Ming & Vitányi, Paul. (1997). An Introduction to Kolmogorov Complexity and Its Applications. 10.1007/978-1-4757-2606-0.
- Randomness, Information Theory, and Kolmogorov Complexity. Yayınlanma tarihi: 27 Nisan 2020. Bağlantı: Randomness, Information Theory, and Kolmogorov Complexity
- Kolmogorov Complexity and Our Search for Meaning. Yayınlanma tarihi: 31 Temmuz 2018. Bağlantı: Kolmogorov Complexity and Our Search for Meaning
Matematiksel





