Büyük sayılar kanunu ya da büyük sayılar yasası, olasılık teorisi ve istatistiğin temellerinden biridir. Uzun vadede, gelecekteki olayların sonuçlarının makul bir doğrulukla tahmin edilebileceğini garanti eder. Bu, finans şirketlerine sigorta fiyatlarını belirleme konusunda güven verir. Aynı zamanda kumarhanelerin müşterilerinden her zaman kâr etmelerini sağlar.
Bir madeni para bir kez havaya atıldığında, tura gelme olasılığının 1/2 olduğu bilinen bir gerçektir. Peki madeni para 50 kez havaya atıldığında ne olur? 25 kez tura mı gelir?
Bu sorunun cevabını ve beraberinde büyük sayılar yasasının nasıl çalıştığını anlamak için bir oyun oynamak istediğimizi varsayım. İki takım olsun. Bir miktar bozuk parayı atıyorsunuz ve en fazla tura atan kazanıyor. Her tura bir puan demek. Ancak herkeste eşit sayıda bozuk para bulunmuyor. Bir gruptaki üyelerin her birinde 10, diğer gruptaki üyelerin her birinde 100 adet madeni para var.
Yukarıda verdiğimiz bilgilere göz atarak oyunu kesinlikle daha fazla madeni paraya sahip olan takımın kazanacağı neredeyse kesindir. Sonuçta yazı tura oyununda tura gelme olasılığı 1/2’dir. Bu durumda bir grup 100 atışta 50, diğer grup da 10 atışta 5 tura atma şansına sahiptir. Bu durum da sonuç adil gözükmüyor. Bununla birlikte ne kadar fazla para atarsanız yüzde 50-50’ye o kadar çok yaklaşırsınız.
1939 yılında Avrupa’ya bir ziyarette bulunan Güney Afrikalı matematikçi John Edmund Kerrich kendini bir anda bir toplama kampında bulmuştu. Bu süreçte bir parayı 10.000 kez atıp tura sayısını kaydederek Büyük Sayılar Yasasını gösterdi. Aslına bakarsanız daha fazla paranızın olması ve daha fazla yazı tura oynamanız daha fazla tura geleceği anlamına gelmez. Turaların sayısı daha fazla para attıkça %50’ye yakınlaşacaktır.
Büyük Sayılar Yasası Nedir?
Yasaya göre, meydana gelen bir olay hakkında daha fazla gözlem yaptıkça, o sonucun ölçülen olasılığı (veya şansı), herhangi bir gözlem başlamadan önce hesaplanan teorik şansa daha da yaklaşır. Başka bir deyişle, çok sayıda denemeden elde edilen ortalama sonuç, olasılık teorisi kullanılarak hesaplanan beklenen değere yakın bir eşleşme olacaktır. Bu durumda deneme sayısının arttırılması, ortalamanın daha da yakın hale gelmesine neden olacaktır.
Bir deney defalarca tekrarlandığında bu deneyin sonuçlarının belirli bir ortalamaya yakınlaştığı anlayışı yeni değildir. Aslında bu neredeyse matematiksel olasılığın kendisi kadar eskidir. Bu prensibin biçimsel olmayan bir formu 16. yüzyılda Girolamo Cordano tarafından ortaya konmuştur.

Büyük sayılar yasası adını veren kişi ise 1800’lerin başlarında Simeon-Denis Poisson olmuştur. On sekizinci yüzyılın başlarında Jakob Bernoulli, Büyük Sayılar yasasının matematiksel ispatını ortaya yapmış sonucunda da bir teorem halini almasını sağlamıştı.
Zayıf ve Güçlü Büyük Sayılar Yasası
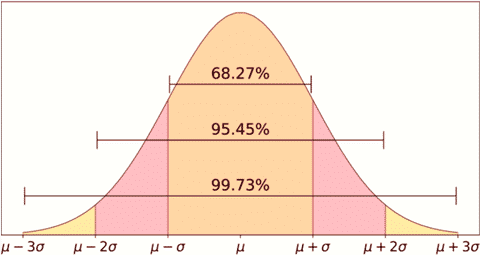
İstatistiksel analizde büyük sayılar kanunu merkezi limit teoremi ile ilişkilidir. Merkezi limit teoremi, örneklem büyüklüğü arttıkça örneklem ortalamasının eşit şekilde dağılacağını belirtir. Bu genellikle çan şeklinde bir eğri olarak gösterilir. Burada eğrinin zirvesi ortalamayı gösterir.
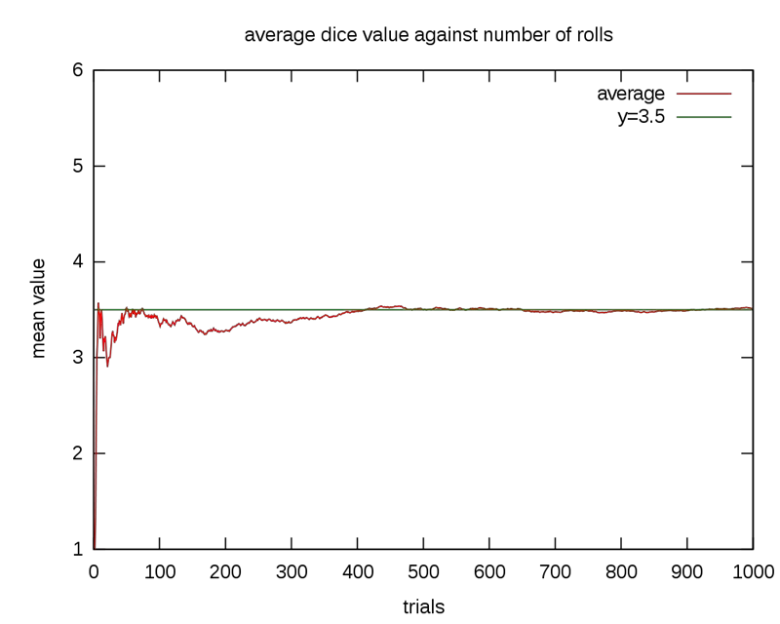
Rastgele dizilerin sınırlayıcı davranışıyla ilgilenen iki büyük sayı yasası vardır. Birine büyük sayıların “zayıf” yasası, diğerine ise büyük sayıların “güçlü” yasası denir. Adil bir zar attığınızda, 1’den 6’ya kadar olan altı sayıdan her biri için eşit şansınız vardır. Bu durunda zarın beklenen değeri ise 3.5’tir. Olasılık teorisinde beklenen değer, bir şeyin olası sonuçlarının olasılığını yansıtan idealleştirilmiş bir ortalamadır. Hesaplama biçimini aşağıda görebilirsiniz.
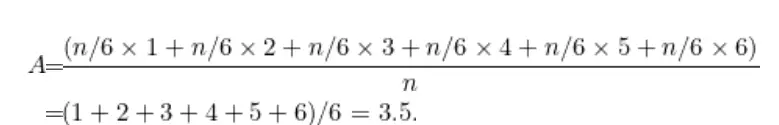
Zayıf büyük sayılar yasasında örneklem ortalaması olasılık sınırları içinde ama bilinmeyen bir olasılıkla ilgili dağılımın ortalamasına yakınsar. Güçlü büyük sayılar yasası ise n büyüdükçe gerçek ortalamanın 3.5’e yaklaştığını söyler. Tahmin ettiğiniz gibi zayıf yasa, güçlü yasa ile karşılaştırıldığında, çok doğru olmayan bir sonuç verir.
Büyük Sayılar Yasasının Algılarımız Üzerine Etkileri
Bu kanunlar sayesinde geleceğe yönelik yapılan kestirimlerde, gerçeği yansıtan değerlere ulaşma şansımız artacaktır. Hayatımızın belli riskler altında sürdüğünü düşünürsek bu kanunların ne kadar işlevsel olduğunu da anlarız. Mesela sosyal medyada sıklıkla karşımıza çıkan kişilik testleri büyük yüzdelere varan başarı oranlarına sahiptir. Belli soruların cevaplarını bizden ister ve cevapları verip testin sonucuna baktığımızda vay be ne kadar da iyi bildi diye düşünürüz. Testlerin başarısı aslında çoklu sayıda veri kullanımının getirdiği başarıdan kaynaklanır.
Bir başka örneği internet alışverişlerimizden verebiliriz. Son aldığımız ürünlere baktığımızda -diğer insanların alışverişlerde edinmiş oldukları benzer ürünlerin bilgisiyle- alınabilecek diğer ürünlerle karşılaşırız. Bir öneri listesi önümüze düşer. Bu da bizi ihtiyacımız olsun olmasın yeni ürünler almaya yönlendirir.
Yine sıklıkla başımıza gelen bir örnek daha var. Uygulamalar üzerinden dinlediğimiz müzik, izlediğimiz dizi veya programların akışında öneriler sekmesiyle izlenme sayıları sürekli karşımıza çıkar. Bu durumun etkisel olarak en basit hali -zaman yönetimi problemi günümüzün artan şikayetlerinden biri- belki de izleyerek zaman kaybetmek istemeyeceğimiz yeni videoları izlememize yol açmasıdır. Hayatımızın içinden verebileceğimiz örnekleri pek çok farklı alanda çoğaltmamız mümkündür. Örneklerin temelinde ise hakkımızda toplanan bilgilerin oluşturduğu bilgi havuzuyla algılarımıza nasıl yön verildiği yatmaktadır.
Bireysel Etkiden Toplumsal Etkiye Uzanış
Bunlar basit ama önemli bir bireysel etkidir. Çünkü algılarımızı ve değer yargılarımızı değiştirmeye yönelik çalışmaları içerir. Aynı stratejinin kullanımının topluma etkisi ise her alanda muazzam ölçüde artmakta ve geleceğimize yön vermektedir.
İstatistik bilimi anlatılmaz ölçüde güzelliklerini, çıkar gruplarının elinde bize karşı olumlu ya da olumsuz yapıda göstermektedir. Bu yüzden ünlü oyuncu Sidney Poitier’ın da dediği gibi dilerim herkes yaptığı çalışmaları, pozitif değerlerinin bir yansıması olarak kullanmayı seçer.
Kaynaklar ve ileri okumalar:
- Maths in a minute: Expectation; yayınlanma tarihi: 20 Mayıs 2016; Bağlantı: https://plus.maths.org/
- What is financial mathematics?; yayınlanma tarihi: 1eylül 2009; Bağlantı: https://plus.maths.org/
- Law of Large Numbers: What It Is, How It’s Used, Examples. Yayınlanma tarihi: Kaynak site: Bağlantı: Law of Large Numbers: What It Is, How It’s Used, Examples
- Falk, Ruma & Lann, Avital. (2013). Numbers defy the law of large numbers. Teaching Statistics. 37. 10.1111/test.12031.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel