Bazen doğru olduğundan şüphelendiğimiz (ama henüz kanıtlayamadığımız) bir şey aslında yanlış olsaydı ne olurdu diye kendi kendimize sorarız. Yanlış olduğuna inandığımız bir şeyin doğru olduğunu varsaymak, temeli Aristo’ya kadar giden eski ve geçerli bir akıl yürütme yöntemidir. Buna reductio ad absurdum, yani olmayana ergi denir.

İspat, bir ifadenin doğru olduğunu göstermeye çalışan mantıksal bir argümandır. İspatlanmayan bir ifade (aksiyom değil ise) matematikçiler tarafından doğru kabul edilemez. Bir şeyi ispatlamanın birçok farklı yolu vardır ancak genellersek doğrudan ve dolaylı olmak üzere ikiye ayrılır. Olmayana ergi, dolaylı ispatlar kategorisinde kendine yer bulur.
Reductio Ad Absurdum Nasıl Çalışır?

Reductio Ad Absurdum, mantıklı bir sonuca varmanın saçmalığını göstererek bir argümanı çürütür. Eğer bir hipotez yanlış bir şeyi ima ediyorsa o zaman hipotezin kendisi de yanlış olmalıdır. Plan şu şekildedir:
- H hipotezinin doğru olduğunu varsayın.
- H’ye göre belirli bir hakikat olan F geçerli olamaz.
- Ancak F geçerlidir.
- Dolayısıyla H yanlıştır
Yani önce yanlış hipotezi geçici, araştırma amaçlı olarak kabul ederiz. Sonra H’nin geçerli olduğu, gerçeğe aykırı zihinsel bir dünyayı kurarız ve devamında realitenin baskısı altında bu dünyanın yıkılışını izleriz. Bu şekilde ifade edince olmayana ergi çok sıradan görünmektedir. Ancak bu yanıltıcıdır. Kullanmaya çok fazla alışmaktan ötürü ne kadar güçlü bir zihinsel araç olduğunu unuturuz.

Reductio Ad Absurdum İçin Bir Örnek
Aslında karekök 2’nin irrasyonel olduğuna dair ispat da basit bir olmayana ergi örneğidir. Bu ispatı yapanı Pisagor’un öğrencilerinden Hippasus, ispat nedeniyle hayatını kaybetmiştir.
- H: karekök 2 rasyonel bir sayıdır. Yani karekök 2, m ve n tam sayı olmak ve ortak bir bölenleri
olmamak üzere, m/n’ye eşittir. - F: m ve n’nin her ikisi de çifttir.
Aslında bunun anlamı, m ve n’nin ikisinin birden çift olamayacağıdır çünkü iki sayının birden çift olduğunu söylemek, 2’nin her iki sayının da bir çarpanı olduğunu söylemekle tam olarak aynı şeydir. Bu durumda da her ikisini de 2 ‘ye bölebiliriz, bu da kesirin en basit terimlerden oluşmadığı anlamına gelecektir.
Şimdi √2 =m/n olduğu için her iki tarafın da karesini alırsak 2=m2/n2 olur. Diğer deyişle veya 2n2=m2 elde ederiz. Bu durumda m2 çift bir sayıdır, yani m’nin kendisi de bir çift sayıdır. Bir tam sayı, ancak başka bir tam sayının iki katı şeklinde yazılabilirse çift sayı olur; dolayısıyla m’yi bir k tam sayısı için m=2k şeklinde yazabiliriz. Bu durumda 2n2=(2k)2= 4k2 olur. Her iki tarafı 2’ye bölersek, n2=2k2 olduğunu buluruz.
Ancak eğer n2 çiftse, n de çifttir. Bu F’nin doğru olduğu anlamına gelir. Yani H’yi benimseyerek gerçek dışı bir şeye ulaşmış oluruz. Dolayısıyla H yanlış olmalıdır. Karekök 2 rasyonel bir sayı değildir.

Asal sayıların sonsuzluğunu da aynı biçimde ispatlayabiliriz. Bu durumda doğru kabul edeceğimiz önerme ‘Sonlu sayıda asal sayı vardır.’ olacaktır. Bu önermeyi doğru kabul ettiğimize göre en büyük asal sayı olmak zorundadır. İlk önce en az bir asal sayı içeren sonlu bir asal sayı listemiz olduğunu düşünelim. Bu listedeki tüm asalları çarpalım ve çıkan sayıya 1 ekleyelim. Bu bulduğumuz sayı listemizdeki asalların hepsinden büyük olduğu için kendisi bu listede değil. Demek ki sonsuz sayıda asal vardır.
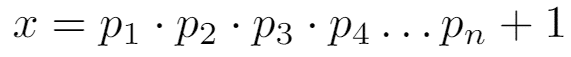
Sonuç Olarak
Matematikteki kalıpları farkında olarak veya olmayarak günlük yaşantımızda kullanırız. Reductio ad absurdum tekniği de bir yönüyle mizah alanında kendini bizlere gösterir: Acayip bir önerme ele alınır. Şaka ya da fıkra bu öncülü saçma bir noktaya kadar geliştirir. Ya da akla uygun ama mecazi anlamda söylenen bir önerme asıl anlamında yorumlanır ve fıkra buna uygun olarak geliştirilir.
Örneğin, bir çok mizah öyküsü “şöyle şöyle olsaydı ne olurdu?” anlamına gelen paragraflarla başlar. Burada “şöyle şöyle olsaydı” tümcesi saçma sonuçları öykünün devamında geliştiren öncüldür. Mizahta vurgulanan şey doğal olarak matematiktekinden farklıdır. Mizahta, öncülüğü saçmalığa indirgemek, öncülü reddetmek amacından çok, saçmalığın kendisi için yapılır. Yine de hicivde olduğu gibi, iki amaç bir arada bulunabilir. Hocanın fıkralarından birine veya birkaçına bu bakış açısıyla bakmak size kalsın….
Kaynaklar ve ileri okumalar:
- Reductio Ad Absurdum in Argument. Kaynak site: yayınlanma tarihi: Thought Bağlantı: Reductio Ad Absurdum in Argument
- Britannica, The Editors of Encyclopaedia. “reductio ad absurdum”. Encyclopedia Britannica, 29 Apr. 2024, https://www.britannica.com/topic/reductio-ad-absurdum. Accessed 16 May 2024.
Matematiksel






