17. yüzyılda İtalyan fizikçi ve matematikçi Evangelista Torricelli sadece barometreyi bulmakla kalmadı. Aynı zamanda adını imkansız bir matematiksel şekil ile ölümsüzleştirdi. Bu şekil günümüzde Torricelli’nin trompeti (diğer adıyla Cebrail’in borusu – İng: Gabriel’s horn) olarak bilinmektedir. Bu şekli ilginç kılan şey ise şeklin sonlu hacme ancak sonsuz yüzeye sahip bir cisim olması.

Galileo’nun öğrencisi Evangelista Torricelli, barometrenin mucidi olarak anılıyor. Aynı zamanda yetenekli bir matematikçiydi ve artık Torricelli’nin Trompet’i olarak adlandırılan basit bir geometrik yüzeyin olağanüstü özelliklerini keşfetti. Ancak sonsuza kadar uzanan bir geometrik formun sonlu bir hacme sahip olabilmesi Torricelli için büyük bir sürpriz oldu.

Torricelli’nin Trompeti Nedir?
Öncelikle bu cismin nasıl elde edildiğine bakalım. Torricelli’nin trompeti, y=1/x eğrisinin x’in 1’e eşit ya da büyük olduğu bölgelerde x ekseni etrafında 360 derece döndürülmesiyle oluşmuş bir üç boyutlu şekildir. Hatırlamayanlar için y=1/x şeklinin grafiği aşağıdaki gibi gözükmektedir.
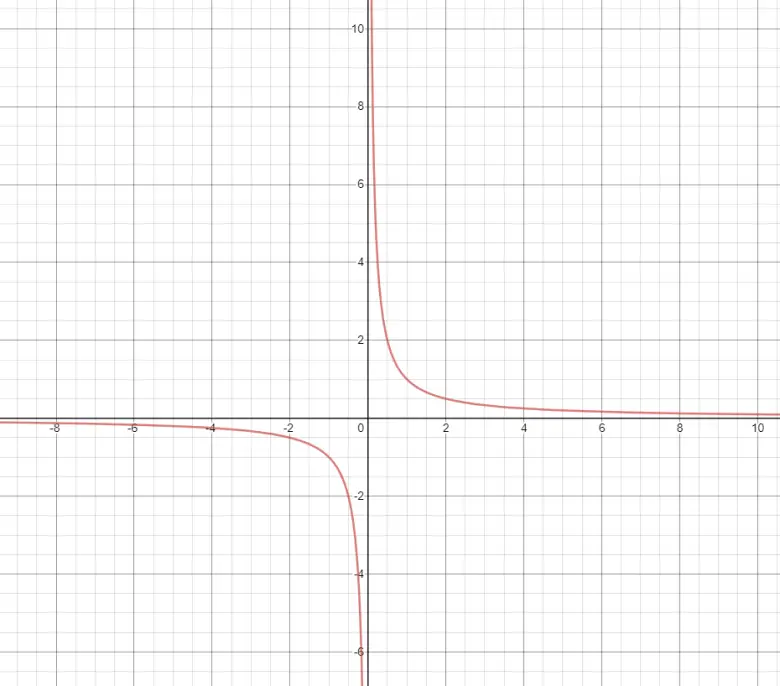
Aşağıda bir örneğini gördüğünüz Torricelli’nin trompeti gibi bir nesnenin gerçekte var olması mümkün değildir. Ancak şeklin sonlu bir hacme, ancak sonsuz yüzey alanına sahip olduğunu göstermek için standart matematik yöntemleri kullanılabilir! Yani bu şeklin ancak matematiksel bir dünyada var olması mümkündür.
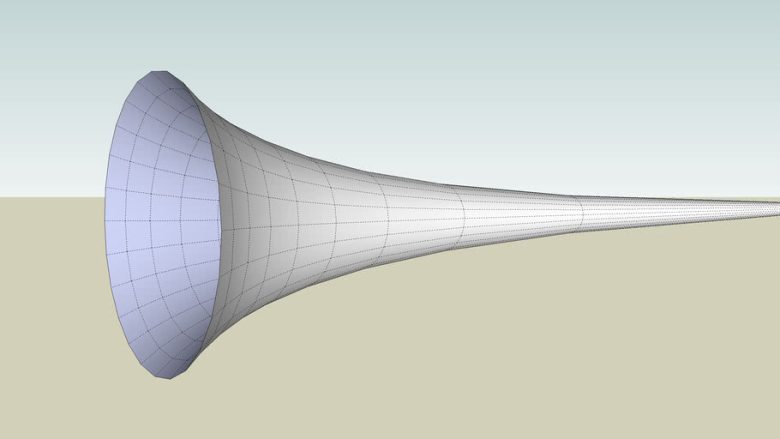
Matematikte sonsuzluk işin içinde dahil olduğunda paradokslar bir biçimde işin içine karışacaktır. Torricelli’nin trompeti de bir paradoks oluşmasına neden olur. Sonucunda x değerine herhangi bir üst sınır koymadan 1/x fonksiyonunun grafiğini döndürdüğümüzde yüzeyi sonsuz olan bir cisim elde ediyoruz. Ayrıca x ne kadar büyük olursa 1/x değeri de o kadar küçük olur.
Örneğin, x = 10 iken 1/x = 0,1 olur; x = 100 iken 1/x = 0,01 olur. Yani x büyüdükçe fonksiyonunun değeri küçülecektir. Bu yüzden x büyüdükçe trompetin ağzı da giderek küçülecektir. Bu durum asla sona ermeyecek diğer bir deyişle de Torricelli’nin trompetinin yüzey alanı sonsuz olacaktır.
Torricelli’nin trompeti sonlu bir hacme sahiptir
Güzel bir mantık ama şaşıracak fazla da bir şey yok diye düşünüyorsanız aslında haklısınız. Zaten asıl şaşırtıcı olan şey yüzeyinin sonsuz olmasına rağmen hacminin sonlu olmasıdır. Şimdi bu yapının hacmini hesaplamaya çalışalım. Şekle farklı bir açıdan baktığımızda, grafiğin temelde birbiri üstünde duran ve boyutları küçülen çok sayıda daireden oluştuğunu fark edeceksiniz. Bu nedenle de aşağıdaki formülü kullanarak tüm dairelerin alanlarını toplayıp, hacmini hesaplamak için integrali kullanabiliriz:
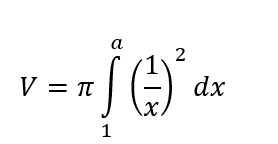
Burada a şu anda sadece bir reel sayıyı temsil etmekte olmakla beraber integrali aldıktan sonra bu a’nın sonsuza giderken limitini alacağız. İntegrali alırsak aşağıdakini elde ederiz.
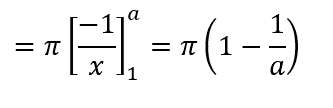
Ve şimdi a sonsuza giderken limit alırsak karşımıza V= π çıkar. Bu durumda şeklin sonlu bir hacme sahip olduğunu görüyoruz! Mantıklı olmayan kısım burasıdır. Bilgimiz bize bir şeklin hacminin grafiğin altında kalan alan ile ilişkili olduğunu söyler. Bu, şeklin hacminin de tanımsız olması gerektiği anlamına gelir. Ancak hacmin sonlu olduğunu kanıtladık. Bu durum da bizi Boyacı paradoksuna ( the Painter’s paradox) götürüyor.
Torricelli’nin trompeti aralarında Thomas Hobbes, John Wallis ve Galileo Galilei’nin de bulunduğu, dönemin pek çok önemli bilim insanının dahil olduğu, sonsuzluğun doğası üzerine tartışmalara neden olmuştu. Sonrasında da bazı çözümlere kavuştuk.
Boyacı Paradoksu Nedir?

Şimdi bir ressam olduğunuzu ve Torricelli’nin trompetini boyamak istediğinizi düşünelim. Şekil sonlu bir hacme sahip olduğu için boyayla doldurmanız mümkün olacaktır. Aslına bakarsanız az önce hacminin Pi kadar olduğunu bulmuştuk. Yaklaşık olarak düşünürsek bu da üç metreküp veya üç bin litre boya gerekir. Peki bu miktarda boya ile şeklin yüzeyini boyamamız mümkün olacak mı?
Ressam paradoksunda şaşırtıcı olan şey, trompetin içini boyayla doldurabilmemize karşın yüzeyini boyayamıyor olmamızdı. Ayrıca daha da kafa karıştırıcı bir durum var. Sonucunda elimizdeki bir koca boyayı şeklimizin içine döktüğümüz zaman şeklimizin iç yüzeyini de boyamış olacağız. Peki ama sonsuz bir şekli sonlu bir şeyler kaplamak nasıl mümkün olacaktır?
Boyacı Paradoksunun Çözümü Nedir?
Matematik, ilk başta inanılmaz gibi görünse de sahip olduğumuz araçları kullanarak çözülmesi mümkün olan benzer birçok paradoksla doludur. Aslında sonsuz bir alanı sonlu hacimde boyayla kaplamak oldukça mümkündür. Bunun bir örneğini anlamak için aşağıdaki görsele bakalım.
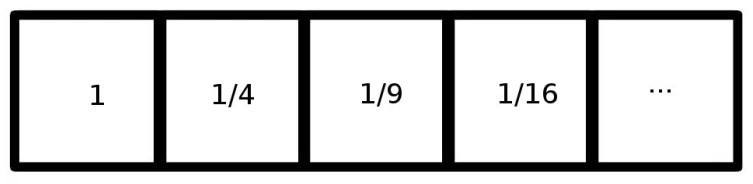
Burada yanyana duran sonsuz sayıda kare görüyorsunuz. İçlerindeki rakamlar da bu karelerin alanlarını gösteriyor. Bu karelerin alanlarının toplamını aşağıdaki gibi göstermemiz mümkündür.
Toplam \, Alan=\sum_{n=1}^{\infty }\frac{1}{n^{2}}Yukarıda gördüğünüz formül Euler tarafından 1734’te çözülen ünlü Basel Problemine aittir. Basel problemi 1644 yılında Pietro Mengoli tarafından ortaya atılmıştır. Sonucun yaklaşık olarak 1.644934’e eşit olduğu Euler tarafından kanıtlanmıştır.
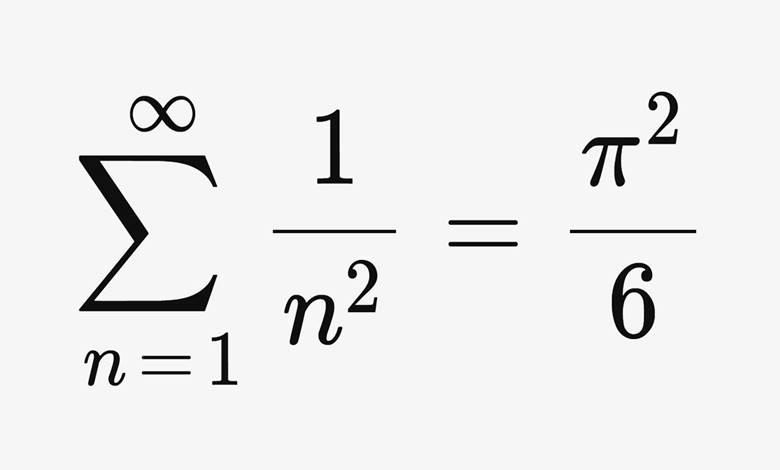
Peki ama bunun ressam paradoksu ile ne ilgisi var derseniz hemen açıklayalım. Bunun için öncelikle Torricelli’nin trompetini aşağıdaki gibi yan yatmış bir doğum günü pastası biçiminde düşünün. Ancak bu doğum günü pastamızın sonsuz büyüklükte olduğunu biliyoruz.
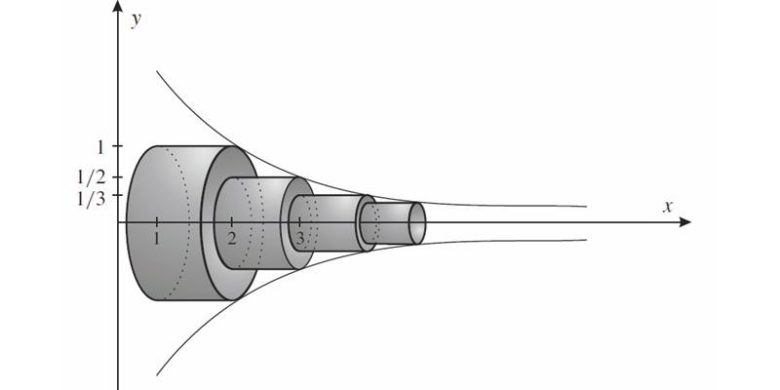
Bu biçimde düşünürsek şekil aslında birim uzunlukları ve yarıçapları sıralı biçimde azalan bir dizi silindirden oluşuyor. Tüm silindirlerin hacimlerini toplayarak hacmi hesaplamak kolaydır ve bu bizi yine Basel problemine götürecektir. Bu durumda toplam hacmin aşağıdaki kadar olması gerektiğini biliyoruz.
V=\pi \sum_{n=1}^{\infty }\frac{1}{n^{2}}=\frac{\pi ^{3}}{6}Öte yandan bu şeklin de yüzey alanı sonsuzdur. Bu, silindirlerin kavisli yüzeylerinin alanları toplandığında kolayca görülebilir. Toplam, ıraksak olduğu iyi bilinen harmonik seridir. Bu silindirlerin alanları toplamı da aşağıdaki biçimde hesaplanabilir.
S=2\pi \sum_{n=1}^{\infty }\frac{1}{n}.1Ancak bu pastayı yan değil de dik biçimde koyduğumuzu düşünün. Bu durumda her bir kat, sanki içiçe geçen bardaklar gibi, bir öncekinin içine girecek ve sonuçta elimizde sadece 1 silindir kalacaktır. Onun da hacmi de Pi kadardır. Yani aslında imkansız gibi gözükse de ortada bir paradoks mevcut değildir.
Sonuç olarak
Aslında son verdiğimiz örnek sonsuz katlı bir düğün pastasına benzediği için Gabriel’in Düğün Pastası (Fleron, 1999) olarak adlandırılmıştır. Bu pastanın sınırlı bir hacmi vardır. Bu nedenle düğüne davet edilenler tarafından tüketilmesi mümkündür. Ancak yüzey alanı sınırsız olduğundan pastanın dışına krema sürülmesi oldukça sorun çıkaracaktır.
Kaynaklar ve ileri okumalar
- Wijeratne, Chanakya & Zazkis, Rina. (2015). On Painter’s Paradox: Contextual and Mathematical Approaches to Infinity. International Journal of Research in Undergraduate Mathematics Education. 1. 10.1007/s40753-015-0004-z.
- Wijeratne, C., Zazkis, R. On Painter’s Paradox: Contextual and Mathematical Approaches to Infinity. Int. J. Res. Undergrad. Math. Ed. 1, 163–186 (2015). https://doi.org/10.1007/s40753-015-0004-z
- Fleron, Julian F., 1999: Gabriel’s Wedding Cake. College Math. Journal, 30, 1, 35-38.
- Torricelli’s Trumpet (or Gabriel’s Horn): A Paradox of Area and Volume; Bağlantı: https://www.youtube.com
- Torricelli’s Trumpet & the Painter’s Paradox. Yayınlanma tarihi: 13 Nisan 2017. Bağlantı: Torricelli’s Trumpet & the Painter’s Paradox
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










