1+1/4+1/9+1/16… şeklinde sonsuza dek devam eden bir toplamın sonucunu aşağıda görüyorsunuz. Peki cevapta neden Pi sayısı var ve neden karesi alınmış durumda? Bu yazıda Pietro Mengoli tarafından ortaya atılan ve Leonhard Euler tarafından çözülen, zamanın matematikçilerini bolca uğraştırmış Basel Problemini öğrenelim.
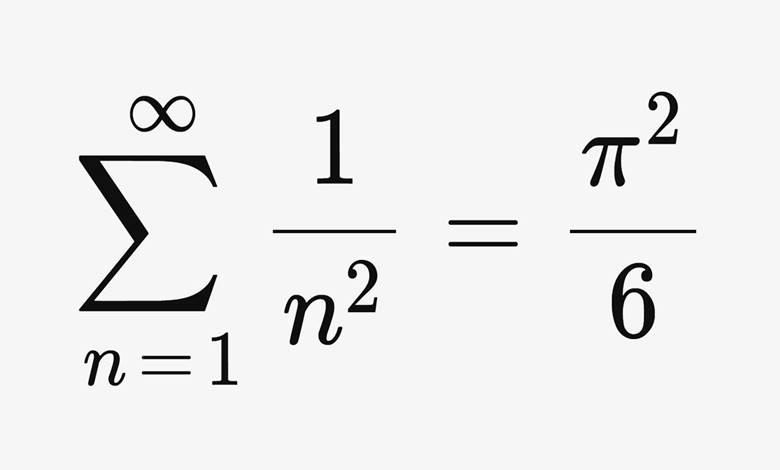
Basel problemi ilk kez 1644’te İtalyan matematikçi Peitro Mengoli tarafından önerildi. Peitro, daha sonra Newton ve Leibniz’in çalışmalarının temelini oluşturacak birçok sonsuz seri ile ilgili çalışmalar yapıyordu. Farklı sonsuz serileri incelerken aşağıda gördüğünüz sonsuz serinin toplamını bulamadı.
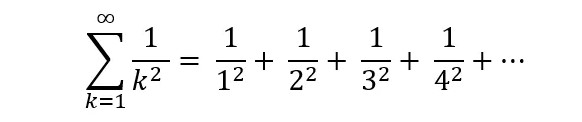
Matematik tarihine göre, Basel Problemi üzerinde çalışan ilk matematikçiler İsviçreli kardeşler Jacob Bernoulli (1654–1705) ve Johann Bernoulli (1667–1748) idi. Yıllar boyunca seriyi çözmeye çalıştıkları halde hiçbir başarı elde edemediler. Leibniz de bu problem üzerinde çalıştı ancak bir çözüm bulamadı.
1721’de Daniel Bernoulli (Johann’ın oğlu) değeri 8/5 buldu ve bunu Goldbach’a bir mektup ile iletti. Bunun üzerine Goldbach mektubuna yanıt vererek değerin kesinlikle 1,64 ile 1,66 arasında olduğunu iddia etti. Bu seri, Basel’de doğan Bernoulli kardeşler ve devamında problemi çözecek Leonhard Euler’in anısına halk arasında Basel problemi olarak bilinmeye başladı.

Basel Problemi İle İlgili Sorun Neydi?
Bu tarz bir problemin çözümü için akla gelen ilk yol elbette daha fazla terim ekleyip sonucu hesaplamaktır. Ancak bu problem ile ilgili en büyük sorun belli bir sayıya çok yavaş yakınsamasıdır. İlk 1000 terimi toplamaya kalkarsanız bulduğunuz sonucun yalnızca ilk iki ondalık basamağı doğru olacaktır. ( Dönemin matematikçilerin bunu el ile yaptığını düşünmek gerçekten takdire şayan).
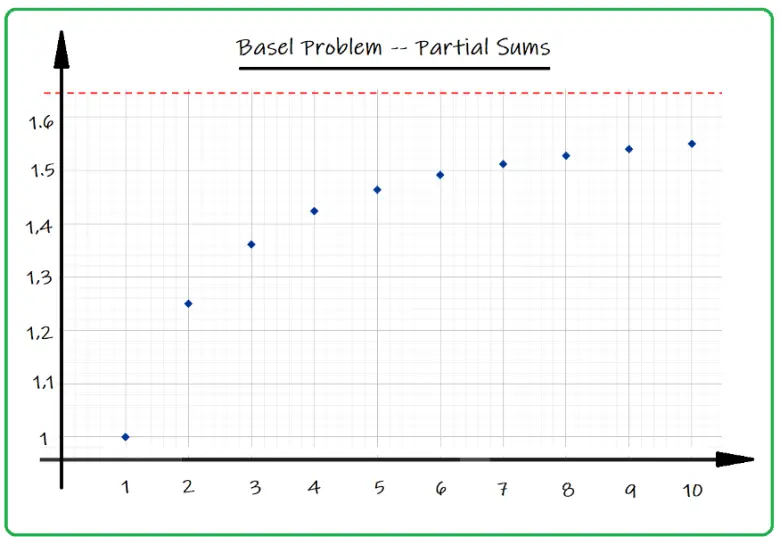
Neyse ki Euler vazgeçmemiş ve 1735 yılında bu sorunun sonucunun π²/6 olduğunu bulmuştu. Pek çok ünlü matematikçi bu problemle uğraşırken, sadece 28 yaşındayken verdiği bu cevap Euler’e matematikçiler arasında bir şöhret kazandıracaktı. Euler daha sonra 1741’de ve 1755’de konu ile ilgili kanıtlarını yayınladı.
Onun kanıtları daha sonra Weierstrass ve Riemann’a analizi ve aşağıdaki şekilde tanımlanan zeta fonksiyonunu geliştirme konusunda ilham verdi. Buda hala matematikte çözülmemiş en önemli problemlerden biri olan Reimann hipotezinin keşfedilmesine yol açtı.
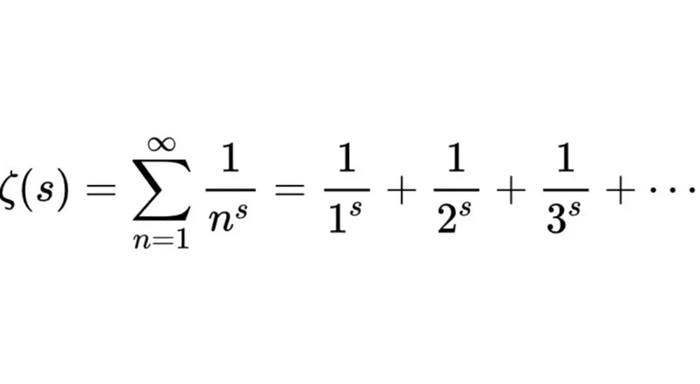
Basel Problemi Çözümü Nedir?
Şimdi Basel probleminin kanıtına göz atalım. Basel problemini çözmenin çeşitli yöntemleri vardır. Euler’in Basel problemine getirdiği çözüm matematiğin gelişimi üzerinde önemli bir etki yarattığı için biz onun çözümünü anlamaya çalışalım.
Öncelikle Euler sinüs fonksiyonunu aşağıdaki gibi gösterdi. Bu gösterim x’in kuvvetleri ile ilgili olduğu için kuvvet serisi olarak bilinir. Bu özel durum da konu ile ilgili çalışmalar yapan Colin Maclaurin’e ithafen (1698 – 1746) Maclaurin serisi olarak bilinmektedir.
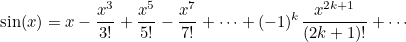
Bildiğiniz gibi herhangi bir ikinci dereceden polinomun kökleri sıfırdan farklı ise, bu polinomu çarpanları cinsinden yazmak mümkündür. Bu nedenle genel olarak aşağıdaki gibi gösterebiliriz. Burada a1,a2…an polinomun kökleridir.
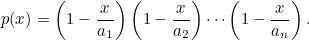
Euler bir p(x) polinomu tanımlayarak başladı. Bu polinomun kökleri sıfırdan farklıydı ve p(0)=1 olmalıydı. Aslında Euler bu aşamada bir varsayımda bulunmuştu. Bu varsayım “Sonlu bir polinom için geçerli olan şey, sonsuz bir polinom için de geçerlidir” biçimindeydi. Bunun sonucunda da aşağıdaki polinomu yazdı. Bu polinom ile de p(0)=1 şartını sağladı.
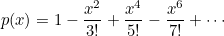
Ardından bu polinomun her iki tarafını da x ile çarptı. Çarpımın sonucuna dikkat ederseniz sin(x) açılımını bulmuş oluyoruz.
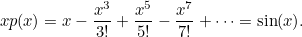
Sinüs fonksiyonu x eksenini 180 derecenin katlarında keser. Bu nedenle de kökleri x= kπ biçimindedir. ( Burada kullandığımız π sembolü bir açı ölçü birimi olan radyanı temsil ediyor.) Burada k=1,2,3…n artı ya da eksi değerler alır. Yani köklerinden biri +π, diğeri –π; bir diğeri +2π diğeri -2π biçimindedir ve bu biçimde devam eder.
Az evvel bir polinomu kökleri cinsinden yazabileceğimizi ifade etmiştik. Bu nedenle de bu kökleri yerlerine yazarak p(x) polinomumuzu aşağıdaki gibi tanımlayabiliriz.
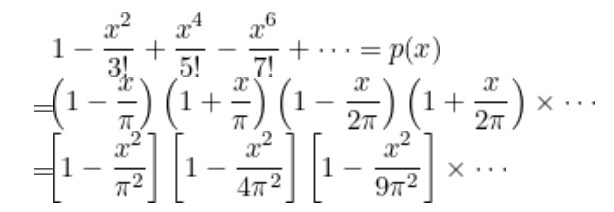
Gördüğnüz gibi Euler’in hilesi p(x) polinomunu iki farklı biçimde tanımlamaktı. Aslında bu aşamadan sonra yapması gereken şey p(x) polinomunun iki farklı biçimini birbirine eşitlemek ve basit düzenlemeler yapmaktı. Sonuç aşağıdaki gibiydi.
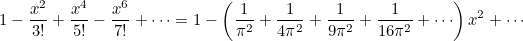
Bu aşamadan sonra yapması gereken x2 li terimlerin katsayılarını karşılaştırmaktı.
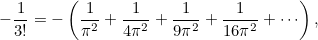
Bu da bize Basel probleminin cevabını verecektir. Sonuç yaklaşık olarak 1.644934’e eşit olur.
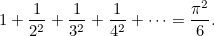
Sonuç olarak
Ancak Euler burada da durmadı. Başka katsayıları da birbirine eşitledi ve başka sonuçlar da elde etti. Yani kendisi sadece Basel problemini çözmedi benzer problemler için de kullanılacak bazı sonuçlar elde etti. Örneğin elde ettiği sonuçların iki tanesi aşağıdadır.

Aslında Euler bu yöntemle k sayısının tüm çift kuvvetleri için bir sonuca ulaşmıştı. Ama tek kuvvetler için bir cevabı yoktu. Bu aslında hala çözülememiş önemli problemlerden biridir. Yani 1+1/ 8+1/27+ 1/64+1/125+1/256… bir sonuca yakınsıyor mu? Bilmiyoruz.
Euler’in kanıtı muhteşemdi ama aynı zamanda o dönemin matematik bilgisi ile açıklanamayan geliştirilen manipülasyonlar kullanmıştı. Euler’in kanıtındaki boşlukların tamamen doldurulması 100 yıl alacaktı. Sonunda Euler’in iddiasını doğrulayacak temel teorileri geliştiren kişi, parlak analist Karl Weierstrass’tı.
Basel Problemi sayı teorisi, karmaşık analiz ve cebirsel geometri arasında derin bir bağlantı kurmuştur. Bazı kriptografi algoritmaları bu problemden faydalanır. Ancak şüphesiz ki en önemli katkısı Reimann hipotezinin keşfedilmesine ön ayak olmasıdır.
Riemann Hipotezi, David Hilbert’in 1900’de yayınladığı çözülmemiş 23 problem listesindeki sekizinci problemdir. Ayrıca Clay Mathematics Institute Millennium Prize Problems (2000) listesinde en önemli ikinci problem olarak yerini korumaktadır.
Kaynaklar ve ileri okumalar:
- An infinite series of surprises; Yayınlanma tarihi: 1 Kasım 2001. Kaynak site: Plus Math. Bağlantı: An infinite series of surprises/
- The Basel Problem: 1 + 1/2² + 1/3² + …… = π²/6 — Two Simplest Proofs. Yayınlanma tarihi: 22 Mayıs 2023. Kaynak site: Medium. Bağlantı: The Basel Problem: 1 + 1/2² + 1/3² + …… = π²/6 — Two Simplest Proofs
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel