Dünyanın en zor ve en ünlü matematik probleminin ne olduğunu belirlemek elbette tam olarak mümkün değil. Ancak, Bernhard Riemann tarafından 1859’da ortaya atıldığından beri matematikçileri şaşkına çeviren Riemann Hipotezi bunun için bir aday gibi gözüküyor.
Riemann Hipotezi, David Hilbert’in 1900’de yayınladığı çözülmemiş 23 problem listesindeki sekizinci problemdir. Ayrıca Clay Mathematics Institute Millennium Prize Problems (2000) listesinde en önemli ikinci problem olarak yerini korumaktadır.
Bu hipotezin çözen kişi elbette adını tarihe yazdıracaktır. Ancak “Milyon Dolarlık Problemlerinden” birisi olduğu için aynı zaman da maddi sıkıntılarını da ortadan kaldıracaktır. Riemann hipotezi özünde asal sayılar daha ziyade asal sayıların sayı doğrusu üzerine dağılımı ile ilgilidir. Riemann hipotezinin cevabı basit bir “evet” veya “hayır”dır, ancak bu cevaba ulaşmanın pek çok varsayımsal yolu vardır ve bunların hepsi son derece zordur. Eğer ispatı doğru çıkarsa bu, uzun yılların en önemli matematik başarılarından biri olacaktır.
Kısaca Riemann Hipotezi Nedir?
Riemann hipotezinin ne olduğunu anlamak için işe asal sayıların ne olduğundan başlamalıyız. Bir matematikçi için asal sayılar atomlar gibidir, yani her sayının yapı taşıdır. Elimizde küçük sayılar olduğunda bu yapıtaşlarını çarpanlara ayırma ile bulabiliriz. Ancak sayılar büyüdükçe bu iş zorlaşır. Ayrıca bir asal sayı bulduktan sonra bir sonraki asal sayının nerede olacağını bilemeyiz. Bu nedenle matematikçiler asal sayıların dağılımlarına bakarlar.

Asal sayılar sayı doğrusuna düzensiz bir biçimde dağılmıştır. Sayılar büyüdükçe, asal sayılar karşımıza daha seyrek çıkmaya başlar. Asal sayı teoremi bize verilen herhangi bir pozitif reel sayıya eşit veya ondan küçük olan asal sayıların sayısını verir. Başka bir deyişle bir pozitif n tamsayısı verildiğinde, n’ye kadar ve n dahil kaç tam sayı asal sayı olduğunu söyler.
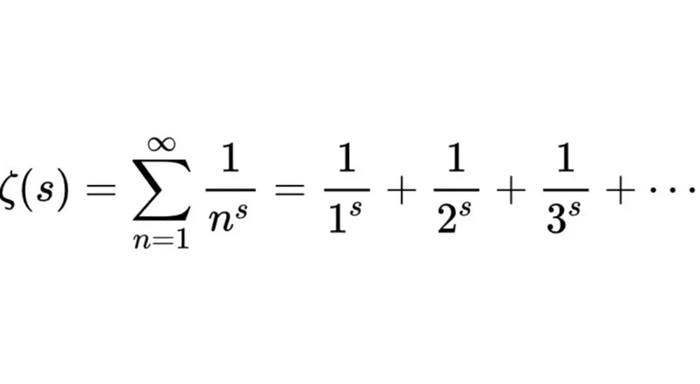
1700’lü yıllarda Leonhard Euler, zeta fonksiyonunu tanımlamayı başardı. Yunan alfabesinin altıncı harfi zetayla (ζ) ile gösterilen bu fonksiyon ζ(s) = 1 + 2–s+ 3–s + 4–s +… biçimindeydi. Euler, zeta fonksiyonunun sonsuz bir çarpıma eşit olduğunu gösterdi. Bu sonsuz çarpımın terimleri ise asal sayılardı. ( Daha fazlası için bu yazıya göz atınız.) Bu asal sayıların dağılımını bulmak konusunda önemli bir adımdı ancak daha fazlasına ihtiyaç vardı.
Riemann Zeta Fonksiyonu Nedir?
1859’da Alman matematikçi Bernhard Riemann (1826–1866) Berlin Akademisi’ne “Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse” başlıklı bir makale sundu. Aslında bu makale onun sayı teorisi üzerine yayınladığı tek makale idi.

Bu makalede Riemann, 1’den büyük değerler için Euler’in zeta fonksiyonu ile aynı olan, ancak daha iyi tanımlanmış bir fonksiyon buldu. Euler’in zeta fonksiyonunu alıp karmaşık sayıları içerecek şekilde genişletti. Fonksiyon bu yeni haliyle Riemann zeta fonksiyonu olarak bilinmektedir.
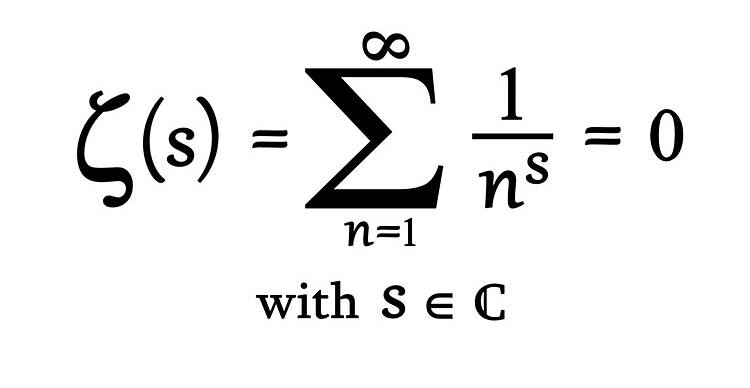
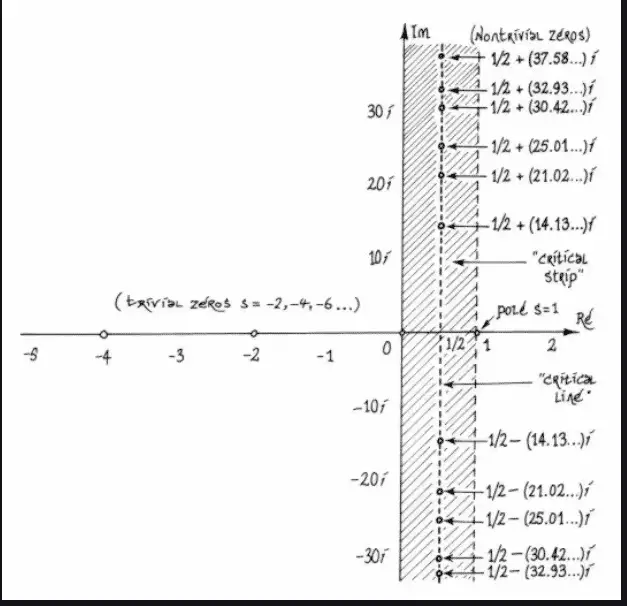
Belirli bir sayıya kadar kaç asal olduğunu tahmin etmek, Riemann zeta fonksiyonunun hangi değerler için sıfır olduğunu bilmeye bağlıdır. Fonksiyon, tüm negatif çift tamsayılar (–2, –4, –6 vb.) için sıfıra gider. Ancak bunlar, asal sayıların nasıl dağıldığı sorununu çözmekle ilgili değildir. Bu nedenle önemsiz (trivial) sıfırlar olarak adlandırılırlar.
Fonksiyonu ayrıca x= 0 ile x=1 arasındaki kritik bölgede sonsuz sayıda sıfır yapan değer vardır. Bugün Riemann hipotezi diye anılan sav bu değerlerin hepsinin karmaşık düzlemde x=1/2 doğrusu üzerinde olup olmadığıdır.
Diğer bir deyişle, Riemann hipotezi, hangi s değerlerinin Riemann zeta fonksiyonunu sıfıra eşitlediğiyle ilgilidir. Bernhard Riemann’a göre bunun bulunması durumunda, sayı doğrusunda herhangi bir aralıkta kaç asal sayının bulunduğunu büyük bir doğrulukla tahmin etmek mümkün olacaktır.
Riemann kurala uyduklarından emin olmak için ilk kontrolleri el ile kendisi yaptı. 1986’da Riemann zeta fonksiyonunun bir buçuk milyar sıfırının x=1/2 doğrusu üzerinde olduğu doğrulandı. ZetaGrid çalıştırdıktan sonra, ilk 100 milyar sıfırın bu çizginin üzerinde olduğu bulundu.
Riemann Hipotezi Neden Önemlidir?
Bilindiği gibi asal sayılar şifrelemenin bel kemiğidir ve güvenliğimiz çoğunlukla büyük asal sayılara bağlıdır. Günümüzde RSA şifrelemesi, çok büyük iki asal sayının çarpılmasıyla oluşturulan sayısal bir anahtar kullanır. Sistemin güvenliği, çok büyük sayıları çarpanlarına ayırmanın zorluğundan gücünü alır.

Riemann Hipotezi asal sayılar dışında görünüşte ilgisiz alanlarda ortaya çok sık olarak çıkar. Bu nedenle, kanıtlamanın (veya çürütmenin) önemi, sayı teorisinin veya bir bütün olarak matematiğin sınırlarının çok ötesine geçer. Riemann hipotezinin atom altı evrenle ince ama doğrudan bir bağlantısı vardır.
Nükleer fizikte, Riemann zeta fonksiyonunun sıfırlarının dağılımındaki düzen ile ağır bir atom olan Uranyum atomunun enerji seviyelerinin dağılımdaki düzen tamamen aynıdır. Bu, kuantum mekaniğinin asal sayılarla bağlantılı olduğu anlamına gelebilir. Bu da başlı başına çılgınca bir fikirdir. Bu nedenle Riemann hipotezi matematikte ilgisiz gibi gözüken konuları birbirine bağlaması açısından önemlidir.
Bir Gün Bir İspat Bulabilecek miyiz?
Riemann’ın hipotezini dünyaya duyurmasının üzerinden 150 yıldan fazla zaman geçti. Bir kanıtın yokluğu matematiğin kalbinde açık bir delik haline geldi. Sayısı tam belli olmasa da muhtemelen yüzlerce araştırmacı bir kanıt bulmaya çalıştı. Ancak şu ana kadar hiçbiri geçerli olarak kabul edilmedi. Ancak yine de çoğu matematikçi Riemann hipotezinin doğru olduğuna inanıyor.
Şu ana kadar yapılan hesaplamalar, kritik çizgide yer almayan hatalı sıfırlar vermedi. Bununla birlikte kontrol edilmesi gereken çok fazla değer olduğu için deneme yanılma ile bir çözüm elde edilmesi mümkün değildir. Bu nedenle matematikçiler genel bir ispata ulaşmaya çalışıyorlar.
Matematikçiler bunu Everest dağına tırmanmaya ve şu anda bir anakampta güç toplamaya benzetiyorlar. Ancak yine de eğer bir gün gerçekleşir ise nihai kanıtın radikal bir fikir gerektireceğini düşünüyorlar. 1900’de matematikçilerin çözmesi için ünlü 23 soru belirleyen David Hilbert, sekizinci soruya ilişkin şöyle demişti. “Eğer 500 yıl uyuduktan sonra uyanırsam, ilk sorum, Riemann hipotezi ispatlandı mı olacak”. Umarız o kadar beklenmek zorunda kalınmaz…
Kaynaklar ve ileri okumalar için:
- What Is The Riemann Hypothesis? And Why Do People Want To Solve It?; yayınlanma tarihi: 22 Temmuz 2021; Kaynak site: Iff Science. Bağlantı: What Is The Riemann Hypothesis? And Why Do People Want To Solve It?/
- Here’s why we care about attempts to prove the Riemann hypothesis. Yayınlanma tarihi: 25 Eylül 2018; Kaynak site: Science news. Bağlantı: Here’s why we care about attempts to prove the Riemann hypothesis. /
- A whirlpool of numbers; yayınlanma tarihi: 1 Mayıs 2003; Bağlantı: https://plus.maths.org
- Has one of math’s greatest mysteries, the Riemann hypothesis, finally been solved? Yayınlanma tarihi: 27 Ekim 2018. Kaynak site: Conversation. The Conversation. Bağlantı: Has one of math’s greatest mysteries, the Riemann hypothesis, finally been solved?
Matematiksel










