Ömer Hayyam dediğimiz zaman çoğumuzun aklına onun kaleme aldığı Rubailer gelecektir. Onun dörtlükleri günümüzde tüm dünyada matematiğe yaptığı katkılardan daha fazla bilinmektedir. Ancak matematik tarihçilerine göreyse, onun ünlü olmasının daha büyük bir nedeni vardır. Hayyam’ın adı kübik denklemlerin çözümünde de yer alır.

Lisede ax2 + bx + c = 0 biçimindeki denklemleri öğreniriz; bunlara ikinci dereceden denklemler denir. İkinci dereceden bir denklemin köklerini bir formül yardımı ile günümüzde kolayca buluyoruz. Aslına bakarsanız bu kökleri neredeyse 3000 yıldır bulmayı biliyoruz. Peki ya üçüncü dereceden denklemler?
Kübik Denklemlerin Kısa Tarihi
Üçüncü dereceden denklemler, a≠ 0 olmak üzere, ax3 + bx2 + cx + d = 0 biçimindeki denklemlerdir. Matematikçiler bu denklemleri çok eski zamanlardan beri bilir. Peki onlar için de benzer formüller kullanmak mümkün müdür?
1494’te İtalyan Rönesans matematikçisi ve Leonardo da Vinci’nin arkadaşı Luca Pacioli Summa de Arithmetica isimli kitabını yayınladı. Bu kitapta, doğrusal ve ikinci dereceden denklemleri çözme yöntemleri yer alıyordu. Ancak kübik denklemleri çözmenin genel bir yönteminin bilinmediğini ve muhtemelen böyle bir yöntemin mümkün olmadığını da belirtmişti. Bu söylem, diğer matematikçileri bir çözüm bulmaya teşvik etti.

Tüm üçüncü dereceden denklemleri çözecek bir yöntem geliştirmek isteyen Ömer Hayyam konikleri kullanarak geometrik bir çözümü bulan ilk kişidir. ( Günümüzde cebir yardımı ile bu denklemi çözmemiz kolay. Ancak modern çağdan önce matematikçiler aynı Ömer Hayyam gibi bu soruyu geometrik bir yaklaşım ile çözmek zorundaydı. ) Ancak kendisi genel bir çözüm bulmayı başaramamıştır. Üçüncü dereceden denklemlerin genel çözümlerinin bulunması hikâyesi de, matematik tarihinin en ilginç hikâyelerinden biridir.
Kübik Denklemlerin Geometri Yardımı İle Çözümü
MÖ 350 civarında Yunan matematikçi Menaechmus, “koni kesitleri” olarak bilinen özel eğriler keşfetmişti. Sonrasında Arşimet bu eğrilerin kuramını geliştirmiş, Pergeli Apollonius ise konuyu Koni Kesitleri isimli kitabında sistemli hale getirip genişletmişti. Ömer Hayyam’ın özel olarak ilgilendiği şey ise bu koni kesitlerinin belirli kübik denklemleri çözümünde kullanılabileceği fikri idi.
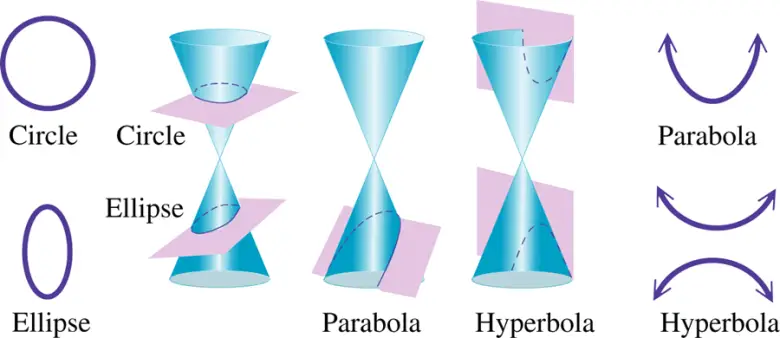
Üç ana koni kesiti türü vardır: Elips, parabol ve hiperbol. Kesen düzlem çift koninin sadece bir yarısından geçtiği takdirde ortaya çıkan kapalı oval eğri bir elipstir. (Çember, elipsin özel bir halidir; düzlem, koni eksenini tam dik kestiğinde oluşur.) Hiperbol, simetrik olarak birbirine bağlı iki açık eğriden oluşmaktadır, kesen düzlem çift koninin her iki yarısından geçer. Parabol ise bir tek açık eğridir ve bu durumda kesen düzlem koni yüzeyi üzerindeki düz-çizgilerden birine paralel olmalıdır.
Bu eğriler bugünün matematiğinde de karşımıza çıkmaktadır. Ancak bu eğriler bir zamanlar, cebirsel açıdan, düz çizgiden sonraki en basit eğriler oldukları için daha da fazla öneme sahipti. Hayyam da bu koni kesitlerinin kübik denklerin çözümünde kullanılabileceğini düşündü.
Ömer Hayyam’ın Kübik Denklemler Üzerine Çalışması

Ömer Hayyam’ın kübik denklemler üzerindeki çalışması, bir kübik denklemin tüm farklı biçimlerinin kapsamlı değerlendirmelerini içeriyordu. Örneğin, x3 + bx = a ve x3 + a = bx’in farklı çözüm yöntemlerine sahip farklı denklem türleri olduğunu kabul etti.
Bunun sonucunda, bir düzineden fazla farklı kübik denklem biçimine çözümler sağladı ve bunları 1079’da tamamladığı kitabında açıkladı. Hayyam’ın bu denklemleri çözme yöntemine bir örneği aşağıda görüyorsunuz. Bu iki eğrinin kesişimi denklemin çözümüdür.
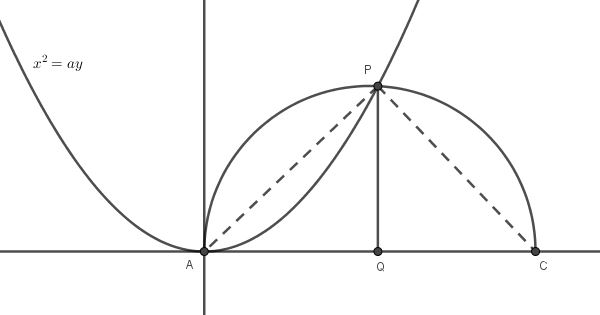
Ancak bir kübik denklemin üç çözümü olması gerektiğini hatırlayın. O günlerde negatif sayılar henüz bilinmediğinden, denklemler tüm terimleri pozitif olacak şekilde düzenlenmişti. Bu nedenle Hayyam sadece gerçek kökler ile ilgili çözümler bulabilmişti. Ancak yine de onun bu girişimi cebirin gelişim sürecinde çok önemli bir atılımdı. Ayrıca göz atmak isterseniz: Titanik’te Yaşamını Yitiren Harry Widener İle Ömer Hayyam’ın İlgisi Nedir?
Kaynaklar ve ileri okumalar:
- Omar Khayyam And The Solution Of Cubic Equations; Bağlantı: https://www.encyclopedia.com/
- Siadat, Vali. (2010). Omar Khayyam: Geometric Algebra and Cubic Equations. Math Horizons. 28. 12-15. 10.1080/10724117.2020.1770495.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










Tebrikler.