Sayıları yazmanın bir çok yolu vardır. Farklı tabanlar, kesirler, ondalık sayılar, logaritmalar içeren aritmetik kullanarak matematiksel düşünceleri ifade edebiliriz. Okul sıralardan hatırlayacağını gibi, her biri farklı bir amaç için kullanılmaktadır. Ancak şaşırtıcı bir şekilde, sayıları göstermenin bir biçimi okullarda öğretilen matematikte göz ardı edilir. Oysa ki sürekli kesirler sayıların en açıklayıcı temsillerinden biridir.

Ondalık açılımları sıradan ve özelliksiz görünen sayıların, sürekli bir kesre açıldığında içlerinde derinlere gömülü olağanüstü simetrilere ve desenlere sahip olduğu ortaya çıkar. Sürekli kesirler ayrıca bize irrasyonel sayılara rasyonel yaklaşımlar oluşturma yolu sağlar.
Sürekli Kesirler Nedir?
Bunlar sayıların gizli özelliklerini ortaya çıkarabilen iç içe geçmiş kesir serileridir. Herhangi bir sayı sürekli kesir olarak yazılabilir. Rasyonel sayılar (tam sayılar dahil) sonlu sürekli kesirler olarak yazılabilir. Çok ilgi çekici olmasa da, aşağıdaki üç örnekte bunun nasıl olası olduğunu görebilirsiniz.

İrrasyonel sayılar sonsuz sürekli kesirlere sahiptir ve bunları sonlu sayıda seviyeden sonra kestiğinizde irrasyonel sayının değerine yakın kesirler elde edersiniz. Yukarıdaki kesirler 𝜋 sayısı için ilk birkaç yaklaşımdır. Çoğumuzun 𝜋 sayısı için alışık olduğu 22 / 7 kesri de, bu biçimde elde edilmektedir. Ancak gerçekte 𝜋 sayısının açılımı aşağıdaki gibidir.
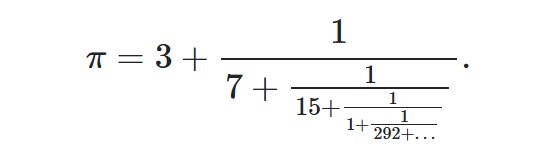
Hintli matematikçi Srinivasa Ramanujan (1887-1920), sayılar ve aralarındaki ilişkiler hakkındaki olağanüstü sezgisiyle ünlüydü. Çarpıcı formüllerden hoşlanıyordu ve ispat etme yükümlülüğü olmadan, sayılara ilginç yaklaşımlarda bulunuyordu.( Sonrasında yazdıklarının hepsinde haklı olduğunu anlaşılacaktı.) Ramanujan özellikle sürekli kesirlere düşkündü.
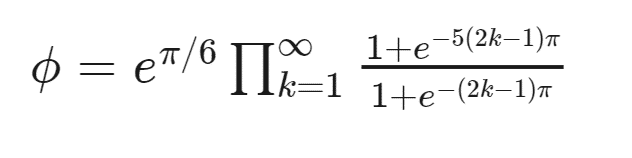
Sürekli Kesirler Nasıl Hesaplanır?
Sürekli kesirler ilk olarak 6. yüzyılda Hintli matematikçi Aryabhata’nın eserlerinde ortaya çıktı. Kendisi bunları doğrusal denklemleri çözmek için kullanmıştı. İlerleyen yıllarda15. ve 16. yüzyıllarda Avrupa’da yeniden ortaya çıktılar ve Fibonacci bunları genel bir şekilde tanımlamaya çalıştı. “Sürekli kesir” terimi de ilk olarak 1653’te Oxfordlu matematikçi John Wallis kullanmıştı.
Aynı zamanlarda, Hollandalı matematiksel fizikçi Christiaan Huygens, bilimsel aletler inşa etmede sürekli kesirleri pratik olarak kullandı. Daha sonra, on sekizinci ve on dokuzuncu yüzyılın başlarında, Gauss ve Euler, bunların birçok özelliğini keşfettiler.
Diyelim ki 72 /19 kesrinin karşılığını bulmamız gerekiyor. İlk iş 72’nin içinde kaç tane 19 olduğunu ve geriye kalanı bulmak olacaktır. Basit bir bölme ile bunu 72= 3 x 19 +15 biçiminde yazabiliriz. Şimdi 19 ile 15 sayısı için aynı işlemi uygulamalıyız.
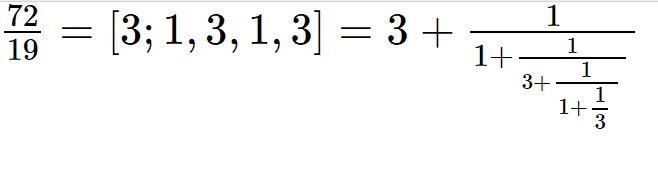
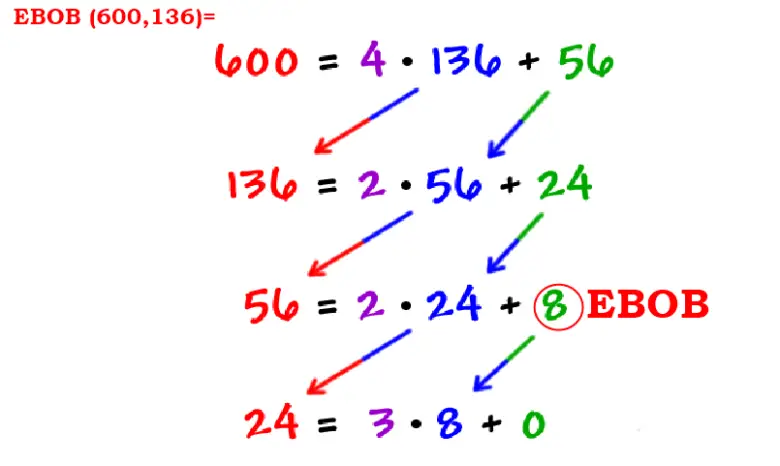
Sonucumuz 19= 1 x 15+4 biçimindedir. Amacımız kalanı sıfır yapmak bu nedenle devam ediyoruz. Şimdi 15 ile 4’e bakacağız. 15=3 x 4+3. Sırada 4 ile 3 var. Sonuç 4=1 x 3 +1 olacaktır. Son olarak 3 ile 1’e bakmalıyız. 3=3 x 1 + 0 olacaktır. 0 sayısını bulduğumuz için artık sürekli kesri yazabiliriz.
Yukarıdaki işlemlerde renklendirdiğimiz sayıları sırasıyla yazarsanız aşağıdaki sürekli kesri elde ederseniz. Bu arada matematik ile arası iyi olan okur, aslında bu bölme işleminin Öklid algoritması olduğunu fark edecektir.
Sürekli kesirler sonlu veya sonsuz uzunlukta olabilir. Genel anlamda bir sürekli kesir aşağıdaki gibi ifade edilecektir.
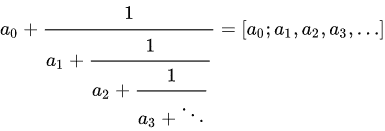
Sürekli Kesirler İle İşlem Yapabilir miyiz?
Evet yapabilirsiniz. Hatta bazı zamanlarda bu kesirler ile işlem yapmamız çok daha kolay olur. Örneğin herhangi bir kesrin çarpmaya göre tersini almak istediğimiz zaman yapmamız gereken şey kesri ters çevirmektir. Devasa bir sürekli kesre sahip olduğumuz zaman bunu yapamayacağımızı düşünmek ise aslında bir hatadır.
Örneğin, 2.3456 ondalık sayısı [2; 2, 3, 1, 3, 4, 5, 6, 4] biçiminde ifade edilecektir. Bu kesrin çarpmaya göre tersini aldığını düşünelim. Yapmanız gereken tek şey aslında başa bir sıfır eklemektir. Bu durumda cevabımız [0; 2, 2, 3, 1, 3, 4, 5, 6, 4] biçiminde olacaktır. Eğer başta sıfır varsa da bu sefer onu kaldırarak tersini alabilirsiniz.
Çünkü irrasyonel sayılar ile hesaplamalar yapmada bazı avantajlar sağlar. Örneğin, 2’nin karekökü ondalık biçim yaklaşık 1.4142135623730951’dir. Ama bunu sürekli bir kesir olarak yazarsanız [1; 2, 2, 2, 2, 2,…] sonucunu elde edersiniz. Diğer bir kaç örneği de aşağıda görebilirsiniz.

İlginç özellikleri olmasının ötesinde bu kesirler bir işe yarar mı? Özellikle bir bilgisayar için cevabımız evet. Bill Gosper bunu 1972 yılında kanıtladı. Kendisi sürekli kesirleri kullanarak günümüzde lazy evaluation olarak adlandırdığımız programlama dilini ortaya koydu. Gosper’in bu çalışması sonucunda, sürekli kesirleri bilgisayar programlarına çok uygun bir biçime dönüştü. Bunun sayesinde bilgisayarlarda istediğimiz hassasiyette işlem yapabiliyoruz.
Kaynaklar ve ileri okumalar:
- Mark C. Chu-Carroll; A Geek’s Guide to the Beauty of Numbers, Logic, and Computation; 2013 The Pragmatic Programmers
- Different ways of looking at numbers; Yayınlanma tarihi: 6 Ocak 2000; Bağlantı: https://plus.maths.org/
- What’s So Great about Continued Fractions? Yayınlanma tarihi: 17 Mart 2015; Bağlantı: https://blogs.scientificamerican.com/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel




Ilgi ve merakla takip ediyorum. Emekleriniz için teşekkürler.
Keşke matematik eğitimi bu sayfadan yapılsa.
Bu arada 55 yaşındayım ve matematik ilgimi doyuran çalışmalarınız için tekrar teşekkür ediyorum.