Bir zeminin uzun, ince ahşap çubuklarla döşeli olduğunu, elinizde bir iğne olduğunu ve iğnenin uzunluğunun ahşap çubukların genişliğine eşit olduğunu düşünün. İğneyi zemine atın. İğnenin, çubukları birbirinden ayıran çizgilerle kesişme olasılığı nedir? Okuduğunuz bu soru Buffon İğne Deneyi olarak bilinmektedir.

Buffon iğne deneyinin hem ilginç bir tarihi hem de ilginç bir sonucu vardır. İşe önce tarihi ile başlayalım. Devamında da bu iğneler yardımı ile pi sayısını hesaplamaya çalışmanın eğlenceli bir yoluna göz atalım.
Buffon İğne Deneyi Başlangıçta İğneler İle İlgili Değildi
Georges-Louis LeClerc Comte de Buffon akademik tutkuları olan bir aristokratı. Önce hukuk okudu ancak mezun olduktan sonra tercihine bilimden yana kullanacaktı. 1733 yılında 27 yaşındayken Paris’te bulunan Kraliyet Bilimler Akademisi üyeliğine aday olmak için hazırdı. Buffon daha sonra doğa bilimci olarak ün kazanacaktı. Devamında da ilgisi soyut matematiğe yoğunlaştı. Sonucunda da geometri ile olasılığı birleştiren ilginç bir makale yazacaktı.

Onu Kraliyet Akademisine götüren makaleyi kaleme alırken aklında Pi sayısını hesaplamak gibi bir düşünce de yoktu. Aslında Franc-carreau adı verilen aşağıda gördüğünüze benzer bir oyunla ilgili düşünüyordu. Oyunun kuralları basitti. Tek ihtiyacınız olan şey madeni bir para ve kare döşemeli bir zemindi. Parayı yere atıyor ve bahse giriyordunuz. Konu şu idi: para tamamen bir karenin içine mi düşer yoksa kenarlara değer mi?
Buffon makalesinde “oyunun her iki oyuncu için de adil olması için karelerin büyüklüğü ne olmalı?” sorusuna bir çözüm sunmuştu. Çözümü de şu biçimdeydi. Eğer madeni paranın yarıçapı r ise ve kare döşemelerin bir kenar uzunluğu L ise, madeni paranın merkezi, bir kenar uzunluğu L – 2r olan daha küçük karenin içinde kaldığı sürece dıştaki asıl karenin kenarlarına değemez.
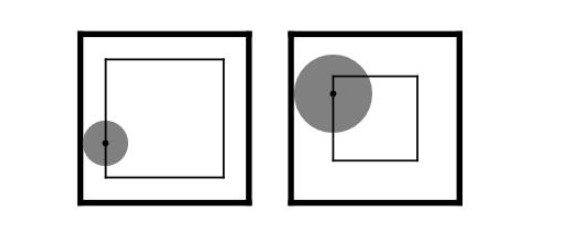
Küçük karenin alanı (L – 2r)2 ve büyük karenin alanı da L2 olduğuna göre; eğer madeni paranın “düzgünce kare içinde” kalacağı üzerine bahse girerseniz, kazanma ihtimaliniz (L – 2r)2/L2 olacaktır. Oyunun adil olması için bu olasılığın 1/2 olması gerekir; bu durumda (L – 2r)2/L2 =1/2 olmalıdır.
Buffon sonunda oyununun adil olması her bir karenin bir kenarının madeni paranın yarıçapının 4 + 2√2 katı olması gerektiğini bulacaktı. Onun bu keşfi günümüzde bize çok anlamlı gelmeyecektir. Ancak olasılıkçı akıl yürütmeyle geometrik şekiller arasındaki ilk ilişki bu biçimde bulunmuştu.
Buffon İğne Deneyi Sonucu Nedir?
Yukarıdaki bilgilerde de gördüğünüz gibi Buffon iğne deneyini Comte de Buffon’un yaptığına dair hiçbir kanıt yoktur. O sadece bir şans oyununun olasılıklarıyla ilgileniyordu. Ne var ki ilerleyen süreçte onun sonuçları matematikçilerin ilgisini çekti ve bu sonuçları pi sayısını hesaplamakta kullanabileceklerini düşündüler.
Şimdi başta sorduğumuz soruya geri dönelim. İğneyi zemine atın. İğnenin, çubukları birbirinden ayıran çizgilerle kesişme olasılığı nedir? Aslında bu soru Buffon’ın makalesinde ele aldığı konudan daha da zordur. Sonuçta iğnenin çizgilerle kesişme ihtimali 0 (iğne eğer çubuklara paralel ise) veya 1 ‘dir. (iğne çubuklara dik ise).

Eğer çubuk ‘rastgele’ bırakılırsa, tahtaların arasındaki çizgiyi geçme olasılığı 2/π olur.
Ancak Buffon’un iğne probleminin beklenmedik bir cevabı vardır: Bu olasılık 2/π veya yaklaşık olarak %64’tür. Ortada herhangi bir çember yokken pi sayısının karşımıza neden çıktığını merak edebilirsiniz. Buffon, cevabını, sikloit adı verilen bir eğri altındaki alanı da kullanarak biraz karmaşık bir şekilde bulmuştu. ( Onun hesaplamasının detayları yazının içinde verilmedi. Ancak kaynaklar kısmından ulaşabilirsiniz.)
1901’de İtalyan matematikçi Mario Lazzarini, Buffon’un iğne deneyini, pi’nin değerini hesaplamak için kullanmayı denedi. İğnesini 3408 kere attı ve iğnenin çizgilere değdiği seferleri sayarak pi’yi altı basamağa kadar doğru olarak hesaplamayı başardı. Fakat bazı matematikçiler bu çalışmaya şüpheyle yaklaştılar.
( Neden tam olarak 3408 atış yapmıştı? Sonuçta pi sayısının gerçek değerini biliyorsanız, tek yapmanız gereken, iğne düşürme deneyinizi doğru sonucu verdiği uygun bir anda bırakmaktır. Bu durumda sonucu aynı kesinlikle ortaya koyan bir deney düzenlemek son derece kolaydır.)

Buffon iğne deneyi Monte Carlo yöntemine de benzer. Monte-Carlo Yöntemi fizik, kimya, mühendislik ve diğer disiplinlerdeki problemlere sayısal yanıtlar elde etmenin en popüler ve yaygın olarak kullanılan yöntemlerinden biridir. Yöntemi ortaya koyan ilk kişi Manhattan Projesi’nde ilk nükleer silahları geliştirmek için çalışan fizikçilerden Stanislaw Ulam’dır. Kendisi bu fikre bir iskambil oyunu analizi esnasında ulaşmıştır.
İlk olarak rulet, zar ve slot makineleri gibi oyunlardaki şans ve rastgele sonuçları modellemede kullanılmıştır. Bu nedenle adını Monako’daki popüler kumar destinasyonundan almıştır.
Monte Carlo Yöntemi İle Pi Sayısının Hesaplanması
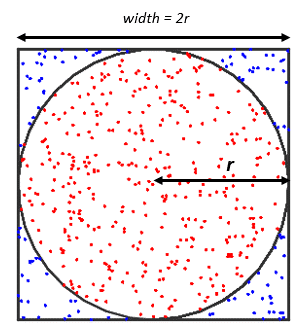
- Bir kare ve karenin kenarlarına teğet bir iç çember çiziniz. Ardından belirli sayıda nokta karenin üzerine eşit ve rastgele olacak şekilde dağıtınız. Sonrasında çemberin içine düşen nokta sayısı hesaplayın.
- Devamında çemberin içinde kalan noktalarla tüm noktalar arasındaki oranı hesaplayın. Bu oran pi sayısının yaklaşık değerini bulmamamıza yardımcı olacaktır.
Şimdi bildiklerimizden yola çıkalım. Sonuçta dairenin alanı πr2‘dir. Karenin alanı ise (2r)2 = 4r2‘dir. Çemberin alanını karenin alanına bölersek π / 4 elde ederiz. Sonucunda kare içindeki nokta sayısı ile daire içindeki nokta sayısı arasında da aynı oran geçerli olmalıdır. Bu sayede çemberin içindeki noktaların sayısının, tüm çemberdeki noktaların sayısına bölümü π / 4 kadar olacaktır.
Sonuç olarak
Ancak bu metodu kullanırken dikkat edilmesi gereken iki önemli durum mevcuttur. Bunlardan ilki noktalama rastgele yapılmadığı takdirde yapılan tahmin tutarsız olacaktır. İkincisi de nokta sayısı az olursa düzgün bir dağılım elde edilemeyecektir. Bunun devamında da doğru sonuca yaklaşmak pek mümkün olmayacaktır. Nokta sayısı arttıkça yaklaşımın doğruluğu artacaktır.
Kaynaklar ve ileri okumalar:
- Buffon was no Buffoon. Yayınlanma tarihi: 13 Ağustos 2015. Kaynak site: Thats Math: Bağlantı: Buffon was no Buffoon
- Franc-carreau or Fair-square. Yayınlanma tarihi: 11 Şubat 2016. Kaynak site: Thats Math: Bağlantı: Franc-carreau or Fair-square
- Buffon’s needle problem; https://en.wikipedia.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





