Okullarda öğretilen matematik genellikle bir gerekçeye ya da kanıta dayanır. Ama matematikte, doğru gibi duran fakat bugüne kadar kimsenin kanıtlayamadığı birçok problem de vardır. Bu tür ifadelere matematiksel hipotez ya da varsayım denir. Genellikle doğru oldukları düşünülür, fakat kesin bir ispatları yoktur. Goldbach hipotezi buna örnektir.

Bir dağcının amacı her zaman daha yüksek bir zirveye ulaşmaktır. Matematikçiler için bu zirve, henüz kanıtlanmamış varsayımları çözmektir. Bu çabanın arkasındaki asıl nedenlerden biri, bazı varsayımların kanıtlanması hâlinde, matematiğin başka alanlarında da önemli etkiler yaratabileceğinin bilinmesidir. Ayrıca bu gibi problemleri çözen kişileri ciddi bir ün de bekler.
Bazı varsayımlar çok sade bir şekilde ifade edilir. Örneğin Fermat, bir defterin kenarına yazdığı kısa bir notla bugün bile konuşulan bir problemi gündeme getirmiştir. Bu tür soruların sadece birkaç sembolle ya da tek bir cümleyle ifade edilebilmesi onları daha ilgi çekici yapar. Benzer bir durum Goldbach hipotezi için de geçerlidir.
Goldbach Hipotezi Nedir?
7 Haziran 1742 tarihinde Alman matematikçi Christian Goldbach, tüm zamanların en büyük matematikçilerinden biri olan Leonhard Euler’e bir mektup yazdı. İlk bakışta sıradan gibi görünen bu mektup, aslında matematik tarihinin en büyük gizemlerinden birini barındırıyordu.
Goldbach, mektubunda şu varsayımı önerdi. İki asal sayının toplamı olarak yazılan her tam sayı, istenildiği kadar asal sayının toplamı olarak da yazılabilir. Bu toplamdaki tüm terimler 1’e indirgenene kadar bu işlem sürdürülebilir.

Bu arada, o dönemde 1 sayısı da asal kabul edilmekteydi.. Yani Goldbach “birimler” dediğinde aslında “birler” demek istiyordu. Mektubun kenarına ikinci bir varsayım daha yazdı. 2’den büyük her tam sayı, üç asal sayının toplamı olarak yazılabilir.
Euler, 30 Haziran 1742 tarihli cevabında, daha önce aralarında geçen bir konuşmayı hatırlattı. Goldbach o konuşmada, ilk varsayımın aşağıdaki ifadenin doğru olması durumunda geçerli olacağını belirtmişti. Her pozitif çift sayı, iki asal sayının toplamı olarak yazılabilir. Bu ifade, Goldbach’ın mektubunun kenarına yazdığı ikinci varsayımla mantıksal olarak eşdeğerdir.
Goldbach’ın mektubunun kenarına yazdığı varsayıma, günümüzde Goldbach hipotezi denir. Modern dilde bu hipotez şu biçimdedir. 2’den büyük her çift sayı, iki asal sayının toplamı olarak yazılabilir. Bu ifadeyi birkaç örnekle test edelim:
- 4 = 2 + 2
- 6 = 3 + 3
- 8 = 3 + 5
- 10 = 3 + 7 = 5 + 5
Goldbach hipotezi, yıllar boyunca birçok matematikçiye ilham kaynağı oldu. Bu problemi incelemek için çeşitli yöntemler ve araçlar geliştirildi. Ancak dünyanın en iyi matematikçileri bile yaklaşık 300 yıldır bu varsayımı ispatlamayı başaramadı. Euler bu konuda şöyle demişti: “Her çift sayının iki asal sayının toplamı olduğunu tamamen doğru bir teorem olarak görüyorum, fakat bunu kanıtlayamıyorum.”
Goldbach Hipotezinin İspatı Nedir?
Goldbach hipotezini belli sayılar için kontrol etmek kolaydır. Hatta bilgisayarlar, bu kuralın en az 4×10 18 sayısına kadar doğru olduğunu doğrulamıştır. Ancak çift sayıların sonu olmadığı için, tüm olasılıkları tek tek kontrol ederek bu önermeyi kesin olarak ispatlamak imkânsızdır.
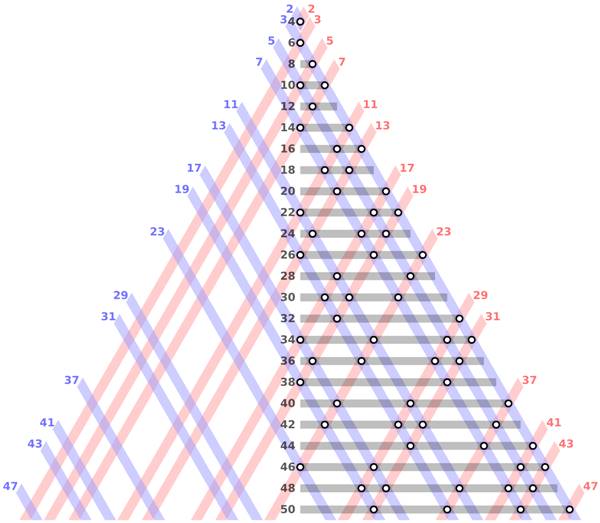
Goldbach hipotezinin ispatı iki farklı biçimde yapılacaktır. Ya iki asalın toplamı olarak yazılamayan bir çift sayı keşfedilecektir ya da birisi neden her çift sayının bu şekilde temsil edilebileceğini kanıtlayacaktır. Pek çok parlak matematikçi bunu kanıtlamayı denedi ve başaramadı. Eğer bir kanıt bulunursa, bu muhtemelen tamamen yeni bir fikir veya yaklaşımı içerecektir.
Aslında belki de olaya bakış açımız yanlıştır. Her matematiksel ifadeyi kanıtlamak mümkün müdür? Alman matematikçi David Hilbert buna inanıyordu. Bu nedenle 1928’de herhangi bir varsayımın geçerliliğini veya aksini kanıtlayacak bir algoritma talep ederek bir meydan okuma ortaya attı. Ancak hayal kırıklığına uğraması kaçınılmazdı.
Kendisine cevap 1931’de mantıkçı Kurt Gödel tarafından verilecekti. Avusturyalı-Amerikalı mantıkçı, matematikçi Kurt Gödel matematiğin hem tutarlı hem de eksiksiz olamayacağını meşhur eksiklik teoremi ile gösterecekti. Neyse ki Goldbach’ın varsayımının matematiğin olağan aksiyomlarına dayanarak kanıtlanamayacağını ileri sürmek için sağlam bir neden yoktur.
Kaynaklar ve İleri Okumalar
- The Subtle Art of the Mathematical Conjecture. yayınlanma tarihi: 7 Mayıs 2019. Kaynak site: Quanta Magazine. Bağlantı: The Subtle Art of the Mathematical Conjecture
- Mathematical mysteries: the Goldbach conjecture. Yayınlanma tarihi: 1 Mayıs 1997. Kaynak site: Plus Math. Bağlantı: Mathematical mysteries: the Goldbach conjecture
- Goldbach’s conjecture: if it’s unprovable, it must be true. Yayınlanma tarihi: 4 Mayıs 2021. Bağlantı: Goldbach’s conjecture: if it’s unprovable, it must be true
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel