Hiç arkadaşlarınızın sizden daha fazla arkadaşı olduğunu düşündüğünüz oldu mu? Eğer cevabınız evet ise bu yazıda size aslında haklı olduğunuzu anlatacağız. Ayrıca, neden çoğu zaman tren veya otobüs için çok uzun süre beklediğinizi, çağrı merkezlerinin neden her zaman meşgul olduğunun da cevabını vereceğiz. Denetleme paradoksu (The inspection paradox) ile tanışın.

İşe öncelik ile arkadaşlarımızdan başlayalım. Gerçekten de çok arkadaşı olan biriyle arkadaş olma olasılığımız, az arkadaşı olan biriyle arkadaş olmamızdan daha fazladır. Aynı zamanda Twitter’da takip ettiğiniz kişilerin sizden daha fazla takipçisi olması ve Facebook’taki arkadaşlarınızın çoğunun sizden daha fazla arkadaşı olması ihtimali de daha yüksektir.
Tam olarak neden bahsettiğimizi açıklamak için bir örnek üzerinden gidelim. 40 kişilik bir sınıftaki öğrencileri ele alalım. Siz de bu sınıfta öğrenci olun. Sınıfınızda, Ayşe’nin sadece bir arkadaşı varsa, sizin o kişi olma olmanız düşüktür. Buna karşılık, Banu sınıftaki öğrencilerin yarısı ile arkadaşsa, o zaman Banu ile arkadaş olma ihtimaliniz daha fazladır.

Her birinin dört arkadaşı olan altı öğrenci ve her birinin 12 arkadaşı olan üç öğrenci olduğunu varsayalım. Bu 9 öğrenciden sadece biriyle arkadaşsanız, arkadaşınızın 12 arkadaşı olan bir kişi olması muhtemeldir.
Bu nedenle, Twitter’da takip ettiğiniz kişilerin sizden daha fazla takipçisi olması ve Facebook’taki arkadaşlarınızın çoğunun sizden daha fazla arkadaşı olması ihtimali yüksektir. Rastgele bir Facebook kullanıcısını seçip ardından arkadaşlarından birini rastgele seçerseniz, onun daha fazla arkadaşı olma ihtimali yaklaşık %80’dir.
Denetleme Paradoksu Nedir?
Denetleme / denetim paradoksu aslında bir paradoks değildir. Bu durum ağlar ve ortalamalar hakkındaki zayıf sezgilerimizden kaynaklanır. Kafanız mı karıştı? İşte başka bir örnek.

Üniversite öğrencilerine sınıflarının kaç kişilik olduğunu sorduğunuzu ve yanıtların ortalamasını aldığınızı varsayalım. Sonuç 90 olsun. Ama resmi sayılara baktığınız zaman ortalama sınıf mevcudu 35 olsun. Bu durumda ya resmi kayıtlar hatalıdır ya da birisi yalan söylüyordur. Aslına bakarsanız her ikisi de değil. Aslında denetim paradoksu iş başındadır.
Bir üniversitede bazı bölüm dersleri büyük sınıflarda bazı bölüm dersleri ise küçük sınıflarda işlenir. Büyük derslerdeki öğrenciler doğal olarak daha büyük sınıf mevcudu ortalamaları bildirirler. Yani bir derslikte 100 öğrenci varsa elinizde 100 ortalama vardır.
Öte yandan bir sınıfta 10 öğrenci varsa, 10 ortalama olacaktır. Bu durumda genele baktığımızda büyük sınıfları daha fazla örneklemiş ve ortalamalarını hesaba katmış olursunuz. Doğal olarak da elde ettiğiniz sonuç daha büyük olacaktır.
Denetim paradoksu en sıradan yerlerde karşımıza çıkacaktır. Örneğin havayolları şirketleri, pek çok uçuşun neredeyse boş olması nedeniyle para kaybettiklerinden şikayet eder. Yolcular da genellikle uçakların çok dolu olmasından şikayetçidir.
Aslına bakarsanız her ikisi de haklıdır. Sonucunda bir uçuş neredeyse boş olduğunda, yalnızca birkaç yolcu bu keyiften yararlanacaktır. Ancak bir uçak dolu olduğunda rahatsızlığı bir çok kişi hisseder. Doğal olarak bir anket yapılsa şikayet edenleri sayısı daha fazla olur.
Aynı durum her aradığımızda bizi beklemeye alan çağrı merkezleri için de geçerlidir. Elbette çağrı merkezinin çalışan eksikliği gibi sorunlar olabilir ancak büyük ihtimal ile sizler de herkes gibi ya öğle tatilinde ya da akşam ebe gittiğinizde arıyorsunuzdur. Doğal olarak olumsuz deneyim yaşayanların sayısı her durumda olumlu deneyim yaşayanlardan fazladır.
Arkadaşlık Paradoksu Denetleme Paradoksunun Özel Bir Durumudur
Şaşırtıcı bir şekilde, yukarıdaki yanılgı her zaman her ağda gerçekleşecektir. Ancak verdiğimiz örneklerin tanıdık gelmiş olma ihtimali de yüksektir. Bunun nedeni denetleme paradoksunun daha popüler bir kavram olan “arkadaşlık paradoksu” nun özel bir durumu olmasıdır.
Sosyolog Scott Feld, “arkadaşlık paradoksu” fikrini ilk kez 1991’de açıkladı. Basit bir hesaplamaya dayanan genel fikir, bir kişinin arkadaşlarının arkadaş sayısının ortalama olarak o kişinin arkadaş sayısından daha fazla olduğudur. Şimdi aşağıdaki çizimi inceleyelim.
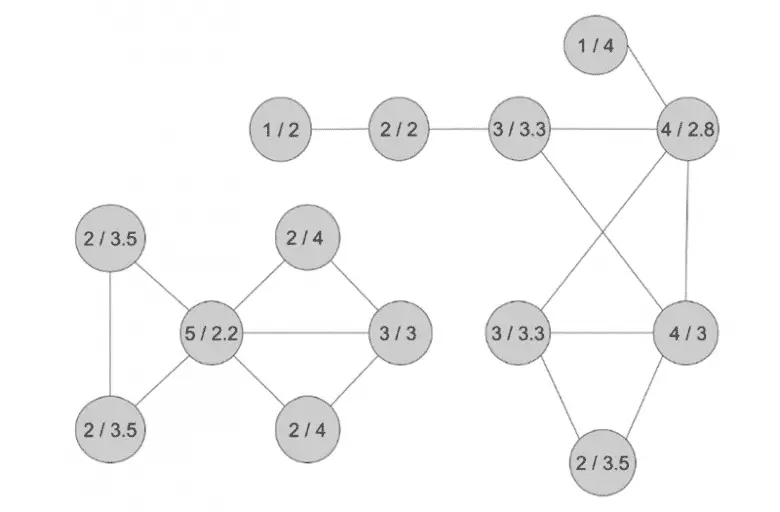
Her daire bir sınıfta bulunan kız öğrenciyi temsil etsin. Toplam 14 kızımız var. Daireler arasındaki çizgiler de iki kız öğrencinin birbiri ile arkadaş olduğunu göstersin. Her kız için listelenen ilk sayı, kızın kaç arkadaşı olduğunu, ikinci sayı da kızın arkadaşlarının sahip olduğu ortalama arkadaş sayısını gösteriyor.
Örneğin sol alt köşedeki kızın 2 arkadaşı var. Bu kızın arkadaşlarının arkadaş sayısı ise 3 ve 4. Bu durumda da ortalamaları da 3,5. Bu durumda bu kızımız arkadaşlarından daha az popüler olduğunu düşünecektir. Listeyi kontrol ederseniz, bu durumun, 14 kızdan 9’u için geçerli olduğunu göreceksiniz. Sadece 3’ü arkadaşlarından daha popüler ve 2’si arkadaşlarının popülaritesine eşit.
Denetleme Paradoksu ve Otobüs Durağında Bekleme Süresi
Denetim paradoksu toplu taşımayı beklerken de yaşanıyor. Otobüs ve trenlerin sabit aralıklarla gelmesi gerekir ancak pratikte bazı aralıklar diğerlerinden daha uzun sürecektir. Diyelim ki bir duraktan belli bir otobüsün ortalama her sekiz dakikada bir geçeceğini biliyorsunuz.

Sonucunda durağa rastgele bir zamanda varırsınız. Bu nedenle kimi zamanlarda yedi dakika 50 saniye boyunca otobüs bekler kimi zamanlarda da varır varmaz otobüse adımınızı atarsınız. Bu durumda ortalama otobüs bekleme zamanınız yaklaşık dört dakika olmalıdır. Ancak ortalama olarak her sekiz dakikada bir otobüs gelmesi, her sekiz dakikada bir geleceği anlamına gelmez
Sonucunda işler her zaman istenildiği gibi gitmez. Otobüsler çoğu zaman trafikte sıkışır kalır. Bu da bazı bekleme aralıklarının daha uzun bazılarının da daha kısa olacağı anlamına gelir. Peki neden kötü şansınız sizi hep uzun aralıklarla vuruyor? Bu kötü şans değil, sadece olasılıktır. Bunun nedenini anlamak için aşağıdaki görseli inceleyelim.
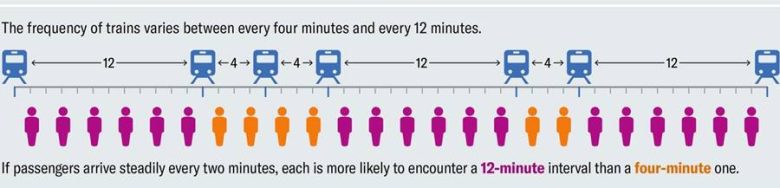
Yukarıdaki zaman çizelgesi otobüsler arasındaki altı aralığı gösteriyor. Bunların yarısı 12 dakika, diğer yarısı ise dört dakika sürüyor. Sonuç olarak size her ne kadar otobüs sekiz dakikada bir gelecek dense de işe gidip gelenlerin sinir bozucu bir bekleme yaşama olasılıkları üç kat daha fazladır.
Sonuç olarak
Gördüğünüz gibi bu paradoks aslında istatistiksel bir yanılsamadır. Bu nedenle araştırmalarda bu önyargılar konusunda dikkatli olmak gereklidir. Bir ölçüm yapılırken neyi ölçtüğünüz ve bunu nasıl raporladığınız konusunda net olmalısınız.
Neyse ki bilim insanları bu yanılsamanın farkındadır ve çalışmalarını hata payını ortadan kaldıracak biçimde yapmaktadır. Bizler de konuyu öğrendiğimize göre, şansımız yaver gitmediğinde hemen kızmak yerine daha farklı bir bakış açısı ile olayı ele alabiliriz. En azından bir sonraki otobüsü beklerken sadece yanlış zamanda durağa vardığınızı anımsayabilirsiniz.
Kaynaklar ve ileri okumalar
- Ross, Sheldon. (2003). The inspection paradox. Probability in the Engineering and Informational Sciences. 17. 47 – 51. 10.1017/S0269964803171033.
- “Why Your Friends Have More Friends Than You Do”, American Journal of Sociology, Vol. 96, №6 (May, 1991), pp. 1464–1477.
- The Inspection Paradox is Everywhere. Yayınlanma tarihi: 5 Ağustos 2019. Kaynak site: Bağlantı: The Inspection Paradox is Everywhere
- Math Explains Why Your Friends Are More Popular Than You. Yyaınlanma tarihi: 18 Ocak 2024. Kaynak site: Scientific Amerikan. Bağlantı: Math Explains Why Your Friends Are More Popular Than You
Matematiksel





