Matematik, MÖ 4. binyılın ortalarındaki yazının ilk dönemlerinden itibaren, Mezopotamya’da aktif bir disiplindi. Ancak elimizdeki çivi yazılı matematik metinlerinin sayısına ve yaşına bakılırsa, antik dönemde matematiğin zirveye ulaştığı dönem Babil medeniyeti zamanıydı.

Babil matematiği özünde uygulamalı bir matematikti. Yani Klasik Yunan matematiğinin aksine, Babil matematiği geometrik şekillere veya matematik teoremlerinin soyut kanıtlarına ağırlık vermemişti. Bunun yerine amaç matematiği günlük hayattaki problemlere bir çözüm için kullanmaktı. Bunu antik tabletlerde yer alan çarpım tablolarından ya da çeşitli basit algoritmalardan anlayabiliyoruz.
Günümüzde Irak’ın civarlarında, Babil’in kayıp şehirlerinden kalma, binlerce kil tablet çıkarıldı. Bunlardan bir tanesi de Si.427 isimli 3700 yıllık bir tabletti. Si.427, satılmakta olan bir arazi parçası ile ilgili. Çivi yazısıyla yazılan tablet, bataklık alanların yanı sıra bir harman yeri ve yakındaki bir kuleyi içeren bir alanı tanımlıyor. Bunlar o döneme ait sıradan bilgiler gibi gelecektir. Oysa ki Si.427’de çok farklı bir şey var. Si.427 tabletinde üç Pisagor üçlüsünün kullanıldığı göze çarpıyor.

Plimpton 322, modern bir trigonometrik tabloya benzeyen Pisagor üçlülerinin bir listesini içeren bir başka antik Babil tabletidir. Plimpton 322 bize bir Pisagor üçlüsünün hangi kenarlarının düzenli olduğunu ve bu nedenle ölçmede yararlı olduğunu söyler. Bu tabletin yazarının gerçek niyetini asla bilemeyecek olsak da, bildiğimiz şey, Babillilerin Pisagor üçlüleri hakkında kendi benzersiz anlayışlarını geliştirdikleridir.
Babil Sayı Sistemi
Babil matematiği hakkında belki de en çok bilinen gerçek, bir altmışlık sayı sistemi kullanmasıdır. 10’luk sistemde 10 ve 10 sayısının katları bizim için basamaktır. Ancak Babilliler gibi 60’lık sistem kullanırsanız basamaklarınız birler, 60’lar, 3600’ler şeklinde olur. Örneğin 4000 sayısı altmışlık gösterimle (1,6, 40) = 1 x 602 + 6 x 60 + 40 x 1 şeklinde ifade edilirdi.

Babilliler matematiksel denklemleri bizim kadar kesin bir şekilde yazamıyorlardı. Sonucunda sonsuzluk kavramını bilmiyorlar ya da değişkenleri ifade eden sembolleri kullanmıyorlardı. Yine de cebiri, ifadeleri çarpanlara ayırma, toplama, çıkarma, çarpma veya bir denklemin her iki tarafını aynı miktarla bölme ve kök alma gibi bugün yaptığımız yöntemlerin çoğunu gerçekleştirecek kadar iyi anlıyorlardı.
Babilliler ayrıca kesir veya oran kavramını da anlamışlardı. Ondalık basamağa karşılık gelen özel bir sembolleri ya da modern kesir gösterimine benzer bir şeyleri yoktu. Ancak yine de kesirler ile temek işlemleri yapabiliyorlardı. Örneğin 4000 yıl kadar önceye tarihlenen bir tablette şu soru yer alıyordu: “Bir karenin alanı eksi, onun bir kenarı 14,30 ediyorsa, bu karenin kenarını bulunuz.”
Ayrıca kendilerinin sıfır sayısını anladıkları, ikinci dereceden denklemleri çözmek için yöntemler geliştirdiklerini hatta üçüncü dereceden denklemleri de çözdüklerini biliyoruz. Peki kareköklerden haberleri olmadan bunu nasıl yapıyorlardı? Buna bir cevap için kolay bir problemi ele alalım. “Bir karenin alanı ile iki kenarının toplamı 24 ise, bu karenin bir kenarını bulunuz” diyen bir tablet bulduğumuzu varsayınız. Bunu aşağıdaki biçimde düşünmemiz mümkündür.
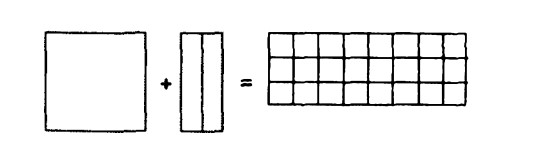
Burada eşit işaretinin solundaki karenin ve dikdörtgenin düşey boyutu bilinmeyene karşılık gelir ve küçük kareler birim boydadırlar. Uzun dikdörtgeni ikiye bölüp iki parçayı karenin yanlarına yapıştırsak, bir köşesi olmayan kare gibi bir şekil elde ederiz. Buradan “kareye tamamlamak” için denklemin her iki tarafına kayıp köşeyi (taralı kare) eklememiz gerektiği görülür.
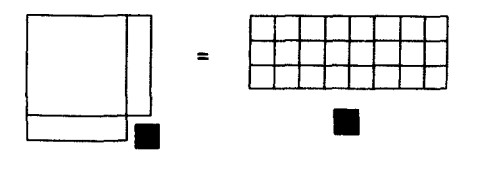
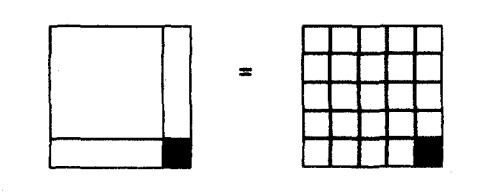
Şimdi solda bir kare ve sağda 25 birim kare var. Bu 25 birim kareyi 5×5’li bir kare şeklinde yeniden düzenleyin. Buradan da bilinmeyenin dört olduğunu bulmak kolaydır.
Babil Matematiğinde Çarpma İşlemi
Babillilerin modern açı kavramına ihtiyaç duymayan tamamen farklı bir trigonometri biçimi de kullanmışlardı. ( Detayları burada:). Tüm bunlar için çeşitli algoritmalar geliştirmişlerdi. Bir örnek olması amacı ile çarpmayı nasıl yaptıklarını inceleyelim.
Şimdi Babilli bir öğrenci olduğunuzu düşünelim. Öğretmeniniz de sizden 23 × 57 işleminin sonucunu hesaplamanızı istesin. Bu durumda ilk olarak 23 sayısının katlarını içeren bir tablete göz atmanız gerekiyordu. Bu tablet aşağıdaki gibi bir şey olmalıydı. ( Tablodaki ondalık sayıların nedeni bu tabletin 60’lık sayma sistemine göre düzenlenmiş olmasıdır. )
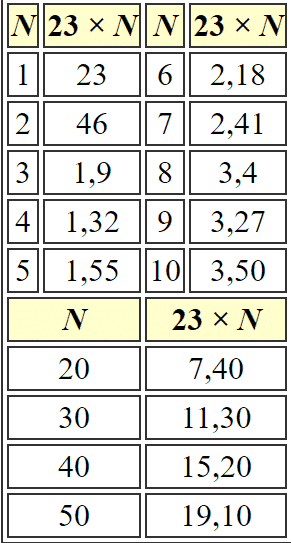
Şimdi, 23 × 57’yi çarpmak için, 57 sayısını 50 + 7 biçiminde yazıyoruz ve çarpmanın toplama üzerindeki dağılma özelliğini kullanıyoruz. 23 × 57 = 23 × (50 + 7) = 23 × 50 + 23 × 7. Sonrada katlar tablosunu kullanarak 23 × 50 = (19,10)60 ve 23 × 7 = (2,41)60. Bu iki sayıyı toplayınca da (21,51) 60 sonucunu elde ediyoruz.
Sonuçta çarpma işleminin toplama haline getirerek cevabı buluyoruz. Kısacası Babilliler çarpma işlemini toplama yardımı ile yapıyorlardı. Ancak bunun için de çok sayıda tablete ihtiyaçları vardı. Belki de bu nedenle ikinci bir yöntem daha geliştirdiler.
Babilliler sayıların karelerini içeren bir tableti nasıl kullanıyorlardı?
Aşağıdaki tablo 60 tabanında 1’den 50’ye kadar sayıların karelerini göstermektedir.
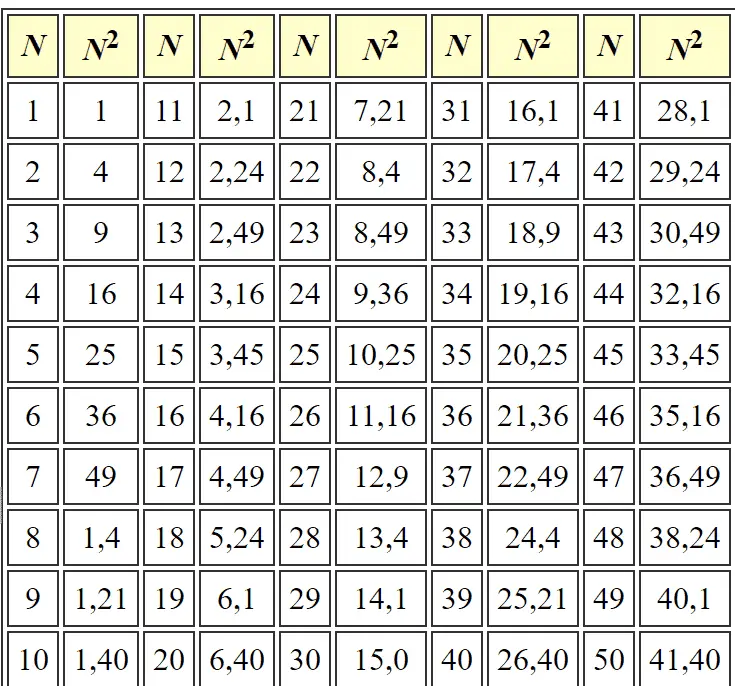
Bu ikinci çarpma yönteminde sayıların karelerinden faydalanmamız gerekiyor. Bunun için de iki özdeşliği bilmeliyiz. Özdeşlikler günümüzde kullandıklarımızın aslında aynısı. Sadece yerleri değiştirilerek düzenlenmiş halleri. (Bunlar benim ne işime yarayacak öğrencilere bu örneği vererek kalplerini fethedebilirsiniz) Şimdi 26 × 14 işleminin sonucunu iki biçim de bulmaya çalışalım.
| x×y = [(x + y)2 − x2 − y2] ÷ 2 | x×y = [(x + y)2 − (x − y)2] ÷ 4 |
| 26×14 = [(26 + 14)2 – 262 – 142] ÷ 2 | 26 × 14 = [(26 + 14) 2 – (26 – 14) 2] ÷ 4 |
| = [402 – 262 – 142] ÷ 2 | = [402 – 122] ÷ 4 |
| = [(26,40)60 – (11,16)60 – (3,16)60] ÷ 2 | = [(26,40) 60 – (2,24) 60] ÷ 4 |
| = (12,8)60 ÷ 2 = (6,4)60 . | = (24,16) 60 ÷ 4 = (6,4) 60. |
Buraya kadar aktardıklarımızın tarihsel değerleri olsa da pratik anlamda işimizi çok kolaylaştırmayacakları aşikar. Ancak iş Babillilerin kullandığı karekök bulma algoritmasına gelince bazı pratik ipuçları edinebilirsiniz.
Babil karekök algoritması
Hero’s method adı ile de bilinen bu karekök alma yönteminde size herhangi bir pozitif S sayısı verilir. S’nin karekökünü bulmak için aşağıdaki adımları uygulamak gerekmektedir.
- Bir ilk tahminde bulunun. Sonuç için herhangi bir pozitif x0 sayısı tahmin edin. Bu ilk tahmini gerçekçi yapmanız önemlidir. Aksi takdirde sonraki basamakları çok defa tekrarlamanız gerekir. Bu nedenle ilk tahmini yaparken özellikle küçük sayılarda tam kare sayılardan faydalanabilirsiniz.
- Tahmini geliştirin. x1 = (x0 + S / x0) / 2 formülünü uygulayın. Sonuçta, x1 sayısı S sayısının kareköküne daha iyi bir yaklaşımdır.
- İşlemi tekrarlayın: xn+1 = (xn + S / xn) / 2 formülünü uygulayın. xn+1 ve xn sayılarının ondalık basamakları birbirine yakınsama sağladığı zaman durun.
Şimdi hemen bir deneme yapalım. 20 sayısının karekökünü virgülden sonra iki basamak olacak biçimde hesaplamaya çalışalım. İlk olarak bir tahminde bulunalım. Diyelim ki ilk tahminde 10 sayısı dediniz. Şimdi hemen bu tahmini geliştirmeye başlayalım ve formülde ilgili yere yazalım.
Bu durumda x1 = (10 + 20/10)/2 = 6 olacaktır. Şimdi işlemi devam ettirelim. x2 = (6 + 20/6)/2 = 4.66667 olacaktır. Şu an ilk iki sonucumuz arasında bir benzerlik yok. Bu nedenle devam etmeliyiz. x3 = 4.47619 ve x4 = 4.47214 sonuçlarını elde ederiz. Gördüğünüz gibi son iki sonucumuzun virgülden sonraki iki basamağı birbirinin aynısı. Bu sayede de 20 sayısının karekökünün yaklaşık olarak 4,47 olduğunu söyleyebiliriz.
Çok büyük sayılar için etkisiz olsa da küçük sayılar ile pratik yapmak için hem ilginç hem de eğlenceli bir yöntem olduğunu düşünüyoruz. Babil matematiği gerçekten incelenmeye değer. Yazının devamında başka karekök algoritmaları için göz atmak isterseniz: Hesap Makinesi Olmadan Karekök Almak İçin İki Basit Yöntem
Kaynaklar ve ileri okumalar için:
- Donald E. Knuth; Ancient Babylonian Algorithms; Bağlantı: https://teaching.csse.uwa.edu.au/
- The Babylonian method for finding square roots by hand; Bağlantı: https://blogs.sas.com/
Matematiksel



