Bir çok kişi karşısına hesaplaması gereken bir karekök alma işlemi çıktığı zaman hesap makinesine sarılacaktır. Oysa ki bu işlemleri hesap makinesini kullanmadan da yapmanız mümkündür.
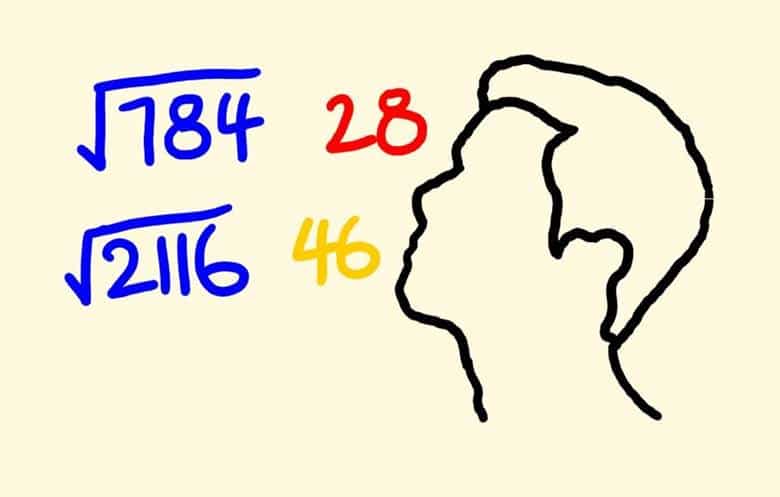
Bazı durumlarda sonuçlar size yaklaşık bir değer verecek olsa da çoğu zaman bu yeterli olacaktır. Bunun için bir çok teknik olsa da bu yazıda iki tanesine yer verelim.
Ancak bu yöntemleri uygularken bir kalem ve kağıda ihtiyacınız olacaktır. Ayrıca tam kare sayılar hakkında da kısa bir bilgi sahibi olmanız da gerekmektedir. Tam kare karekökü bir doğal sayı olan tam sayılara denir. Diğer bir deyişle, kendiyle çarpılan doğal sayıların sonucu tam karedir. 0, 1, 4, 9, 16, 25, 36, 49… ilk tam kare sayılara örnektir. Bu girişten sonra şimdi hesaplamalara geçebiliriz.
1. Karekök Alma Yöntemi
Bir tam sayının karekökünün yaklaşık değerini sadece bir toplama ve bir bölme işlemi ile bulmanız mümkündür. Büyük sayılar için bu yöntem fazla kullanışlı olmasa da özellikle küçük sayılar için hızlı bir sonuç elde etmenizi sağlayacaktır.
Gayet basit olan bu yöntemi bir örnekle açıklayalım. Diyelim ki 120’nin karekökünün yaklaşık değerini bulmak istiyoruz. Bunun için yapacağınız işlem öncelikle 120 ile ona en yakın tam kare sayı olan 121’i toplamak olacaktır. Sonrasında da bulduğumuz toplamı, tam kare sayının (yani 121’in) karekökünün iki katına bölüyoruz. Bu kadar! Aşağıda bu yöntemin genellemesini görebilirsiniz.

Peki, bulduğumuz bu sonuç iyi bir yaklaşım mı? Yani kaç basamağı doğru? 120 sayısının karekökünü bir hesap makinesi ile hesaplarsanız yaklaşık olarak 10,9544… sonucunu elde edersiniz. Aşağıdaki sonucumuz ile gerçek değeri karşılaştırırsak virgülden sonra üç basamağın doğru olduğunu görüyoruz. Bu da oldukça iyi bir tahmin.
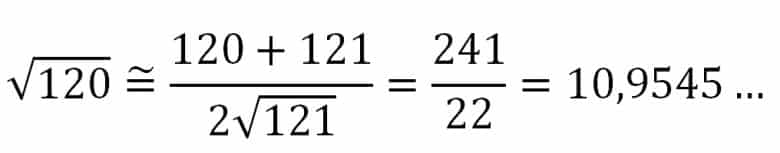
Ancak, her zaman böyle olmuyor. Örneğin 132’nin karekökünü alalım. Bu sayının karekökü yaklaşık 11,489… biçimindedir. Ancak az önce aktardığımız biçimde yaparsak yani 132 sayısına en yakın tam kare sayı olan 121’i alıp hesaplarsak sonucumuz aşağıdaki gibi olacaktır. Bulduğumuz değere oldukça yakın olmasına rağmen, gördüğünüz gibi bu sefer ilk basamakta hata çıktı.
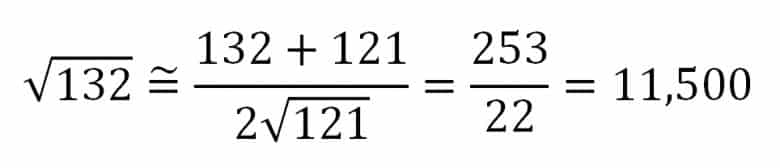
Peki, bu yöntemle bulduğumuz değerin ne zaman iyi ne zaman kötü bir yaklaşım olduğunu söyleyebilir miyiz? Biraz inceledikten sonra şunu görüyoruz ki karekökü alınan sayı bir tam kareye ne kadar yakınsa, yöntem o kadar iyi sonuç veriyor.
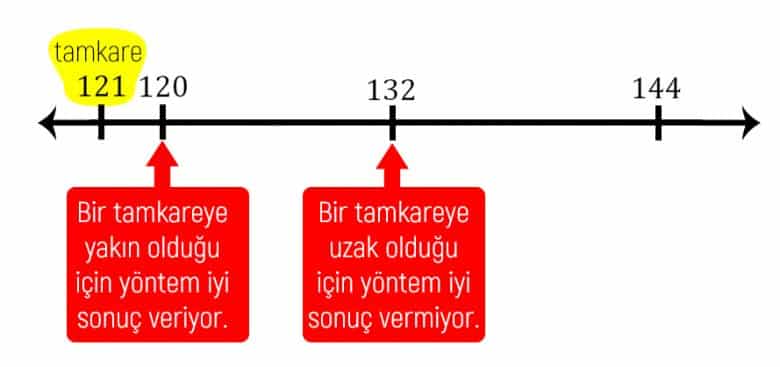
Dikkat ederseniz yukarıdaki örnekte 120 sayısı bir tam kare olan 121’e çok yakın. Gelgelelim 132 sayısı aralarında bulunduğu iki tam karenin ikisine de (121 ve 144) uzak, bu yüzden de daha kötü bir sonuç veriyor. Bunu aşağıdaki görselle daha iyi anlayabiliriz. Şimdi ikinci yönteme geçebiliriz.
2. Karekök Alma Yöntemi
Bu yöntem diğer yönteme göre ilk bakışta daha uzun gibi gözükse de genel anlamda daha kullanışlı. Anlatmak yerine örnek üzerinde açıklamak daha kolay olacaktır. Diyelim ki 529 sayısının karekökünü hesaplamanız gerekiyor.
Öncelikle sayıyı her birinde iki rakam olacak biçimde sağdan sola doğru gruplamak gerekiyor. Bu durumda 5_29 biçiminde sayıyı parçaladık. İki grubunuz olduğu için elde edeceğiniz cevap virgülden önce iki basamak içerecek.

Öncelikle ilk grubumuza bakalım. Bu grupta elimizde 5 sayısı var. Bu sayıdan daha küçük en yakın olan tam kare sayı ise 4 sayısı. Bu durumda aradığımız cevap 4 sayısının karekökü olan 2 sayısı ile başlıyor. Şimdi 2 sayısının iki katını alın ve çıkan 4 sayısını görseldeki gibi bir yere not edin. Ardından da 5-4=1 işlemi ile kalanı bulun ve ikinci grubun başına yazın.
Bu durumda sayımız 129 oldu. Şimdi 12 sayısını not ettiğimiz 4 sayısı ile bölmeliyiz. Bu durumda 12 ÷ 4 = 3 işleminden elde edeceğimiz bölüm aradığımız cevabın 2. basamağı olacak, kalan 0 sayısını ise tekrardan kullanacağız.
Bu sıfır sayısını henüz kullanmadığımız 9 sayısının önüne ekleyeceğiz. Bu durumda da elde edilen 09 sayısını az evvel bulduğumuz 3 sayısının karesinden çıkarmamız gerekiyor. Kalan olmadığı için işlem tamamlanmıştır. Aradığımız cevap 23 sayısıdır.
İkinci Bir Örnek Yapalım
Şimdi 4624 sayısının karekökünü almaya çalışalım. Öncelikle ikişerli gruplara ayırdık. 46_24. Soldaki gruba (46) baktık ve en yakın ancak bu sayıdan küçük tam kare sayıyı bulduk yani 36. Bu durumda ilk basamağımız 6 olduğunu bulduk. Şimdi 6 sayısının 2 katını alalım ve aşağıdaki görseldeki gibi bir yere not edelim.
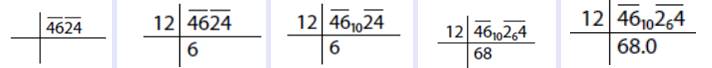
Şimdi çıkarmayı yapıp ( 46-36=10 ) elde ettiğimiz sonucu ikinci grubun önüne yazacağız. Bu durumda 1024 sayısını elde ederiz. Bu aşamada not ettiğimiz sayıyı kullanarak 102 ÷ 12 = 8 ve kalan 6 buluyoruz. Bulduğumuz 8 aradığımız ikinci basamak.
Kalanı ise tekrardan kullanmadığımız 4 sayısının önüne yazacağız. Son olarak bulduğumuz yeni sayımız 64’ten bulduğumuz ikinci basamağın karesini yani 64 sayısını çıkartıyoruz. Kalan olmadığı için cevap bulunmuştur. Aradığımız cevap 68 sayısıdır.
Son Bir Örnek Daha Yapalım
Bu sefer tam kare olmayan bir sayının karekökünü alalım. Sayımız 2656 olsun. İkişerli gruba ayırdık ( 26_56) ardından ilk gruptaki sayıdan küçük en yakın tam kare sayıyı seçtik. (25). Bu sayıyı 26 dan çıkarttık ( 26-25=1). Elde ettiğimiz kalanı ikinci grubun başına yazdık. 25 sayısının karekökünü ise 2 ile çarpıp bir yere not ettik.
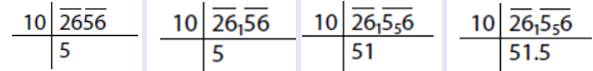
Şimdi 15 sayısını 10 sayısına böldük. Bölüm aradığımız ikinci basamak oldu. Aslında işlemi burada bile kesebilirsiniz. Sonuçta bu sayının karekökünün yaklaşık olarak 51 olduğunu artık anladık. Ancak devam edelim derseniz, kalanı kullanmadığımız 6 sayısının yanına yazmamız gerekiyor.
Sonrasında da ikinci sayımızın karesini yani 1 sayısını, yeni sayımız olan 56’dan çıkarmamız lazım. Bu durumda 56 − 1 = 55 sonucunu elde ederiz. Bu sonuç sıfır çıkmadı. Şimdi ondalık kısma geçme zamanı. İşlem kolay. Aynı biçimde 55 ÷ 10 = 5 ve kalan 5 hesaplayacağız. Bölümden elde ettiğimiz 5 sayısı bizim virgülden sonraki ilk basamağımız olacaktır.
Aradığımız cevap aslında 51,536… biçimindedir. Ancak yukarıdaki yöntemle elde ettiğimiz çözüm makul derece yakındır ve çoğu durumda da bu yeterlidir. Biraz pratik ile kendinizi karekök alma işleminde geliştirebilirsiniz. Ayrıca bu egzersizler öğrencilerin işlem yeteneğini geliştirmek açısından da faydalı olacaktır.
Kaynaklar
How To Calculate Square Roots – Numerals That Changed Math Forever. Kaynak site: Youtube. Bağlantı: How To Calculate Square Roots – Numerals That Changed Math Forever
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel