Olasılık dağılımı, bir değişkenin farklı sonuçlarının ya da değerlerinin ne kadar olası olduğunu tanımlayan matematiksel bir fonksiyondur. Bu fonksiyon genellikle bir grafikle ya da olasılık tablosuyla gösterilir. Deneyin ya da rastlantısal bir olayın olası tüm sonuçlarını ve bunlara ait olasılıkları temel alarak çeşitli sonuçların ihtimallerini sunar.

Olasılık Dağılımına Neden İhtiyaç Duyarız?
Olasılık dağılımları, birçok alanda ve uygulamada kullanılan çok yönlü araçlardır. Temel işlevleri, verideki belirsizlikleri ve değişkenlikleri modellemek ve nicel olarak ifade etmektir. Bu nedenle veri bilimi, istatistik ve karar verme süreçlerinin vazgeçilmez bir parçasıdır. Olasılık dağılımları, farklı sonuçların ya da olayların gerçekleşme olasılıklarını tanımlayarak veriyi analiz etmemizi ve anlamlı çıkarımlar yapmamızı sağlar.
Diyelim ki bir üniversitede öğretmensiniz. Bir hafta boyunca ödevleri kontrol ettikten sonra tüm öğrencileri notladınız. Bu kâğıtları üniversitedeki veri giriş görevlisine verdiniz ve ondan tüm öğrencilerin notlarını içeren bir tablo oluşturmasını istediniz.
Ancak görevli yalnızca notları kaydetti, notların hangi öğrenciye ait olduğunu yazmadı. Ayrıca telaşla başka bir hata daha yaptı; bazı not girişlerini atladı ve hangi öğrencilerin notlarının eksik olduğunu bilmiyoruz.
Bu sorunu çözmenin yollarından biri, notları görselleştirmek ve veriyi gözlemlemektir. Çizdiğiniz grafik, verinin frekans dağılımını gösterir. Grafikte, veriyi tanımlayan düzgün, eğriye benzer bir yapı oluştuğunu görebilirsiniz. Ama bir gariplik fark ettiniz mi? Belirli bir not aralığında anormal derecede düşük bir frekans var. Bu durumda en iyi tahmin, o çöküntüyü oluşturan bölgede eksik veri olduğu yönünde olur.
Gerçek hayattaki bir problemi veri analiziyle çözmeye çalışmak işte böyle bir şeydir. Dağılım, ister veri bilimcisi, ister öğrenci ya da uygulayıcı olun, mutlaka bilinmesi gereken bir kavramdır. Çünkü analiz ve çıkarımsal istatistiklerin temelini oluşturur.
Olasılık dağılımları yalnızca veri analiziyle sınırlı değildir. Mühendislik, çevre bilimleri, epidemiyoloji ve fizik gibi pek çok farklı alanda da güvenilir modelleme, simülasyon ve tahmin yapmayı sağlarlar. Bu yönüyle, bilinçli karar alma ve etkili problem çözme süreçlerine doğrudan katkıda bulunurlar.
Olasılık Dağılımlarının Türleri Nelerdir?
Dağılımları açıklamaya geçmeden önce, ne tür verilerle karşılaşabileceğimize bakalım. Veriler kesikli veya sürekli olur.
Kesikli Veri (Discrete Data), adından da anlaşılacağı üzere yalnızca belirli değerleri alır. Örneğin bir zar attığınızda elde edebileceğiniz sonuçlar yalnızca 1, 2, 3, 4, 5 ya da 6’dır—1.5 ya da 2.45 gibi ara değerler mümkün değildir. Bu tür veriler için kullanılan dağılımlara kesikli olasılık dağılımları denir.
Sürekli Veri (Continuous Data) ise belirli bir aralık içindeki herhangi bir değeri alabilir. Bu aralık sonlu ya da sonsuz olur. Örneğin bir kızın kilosu veya boyu, ya da bir yolun uzunluğu sürekli veriye örnektir. Kilo 54 kg, 54.5 kg ya da 54.5436 kg olabilir. Bu tür veriler için kullanılan dağılımlara sürekli olasılık dağılımları denir. Şimdi dağılım türlerine geçelim.
Bernoulli Dağılımı
Hadi en basit dağılımla başlayalım: Bernoulli Dağılımı. Kulağa karmaşık gelse de anlaması oldukça kolay! Bernoulli dağılımı, yalnızca iki olası sonuca (başarı ya da başarısızlık) sahip tek bir denemeyi ifade eder. Yani, Bernoulli dağılımına sahip rastgele bir değişken X, yalnızca iki değer alabilir:
- 0 (başarısızlık), gerçekleşme olasılığı 1 – p
- 1 (başarı), gerçekleşme olasılığı p
Bernoulli dağılımına birçok örnek verilebilir. Örneğin, yarın yağmur yağıp yağmayacağı. Bu durumda yağmur yağması başarı, yağmaması ise başarısızlık olarak kabul edilir. Bir diğer örnek ise bir oyunun kazanılması ya da kaybedilmesidir. Kazanmak başarıyı, kaybetmek ise başarısızlığı ifade eder. Bu tür olayların ortak noktası, yalnızca iki olası sonucun bulunmasıdır: başarı (1) veya başarısızlık (0).
İki zar atarsanız ve gösterdikleri sayıları toplarsanız, 11 olası sonucunuz olur. (2’den 12’ye kadar olan sayılar). Ancak hepsinin olasılığı eşit değildir. Birçok farklı kombinasyon size nihai sonucu 7 (1 ve 6, 2 ve 5, vb.) verebileceğinden, 7 ile sonuçlanma olasılığınız 2 ile sonuçlanmaktan çok daha olasıdır.
Uniform (Düzgün) dağılım
Tüm sonuçların eşit olasılıkla gerçekleştiği bir olasılık dağılımı türüdür. Bir iskambil destesi, bu dağılıma iyi bir örnektir. Çünkü kupa, maça, karo ya da sinek çekme olasılığı eşittir. Aynı şekilde, yazı tura da uniform dağılıma uyan bir durumdur; çünkü yazı gelme olasılığı da, tura gelme olasılığı da aynıdır. Bernoulli Dağılımından farklı olarak, düzgün bir dağılımın n sayıdaki olası sonucunun hepsinin olasılığı eşittir.
Uniform dağılım, bir grafikle gösterildiğinde düz bir yatay çizgi şeklindedir. Örneğin bir madeni para atıldığında, yazı veya tura gelme olasılığı %50’dir (p = 0.50). Bu durumda grafik, y ekseninde 0.50’ye karşılık gelen yatay bir çizgiyle gösterilir.

Uniform dağılımın eğrisine ait grafik, yukardaki gibi görünür. Grafiğe bakıldığında, uniform dağılımın şeklinin dikdörtgen olduğu görülür. Bu nedenle uniform dağılıma “dikdörtgen dağılım” adı da verilir. Çünkü tüm olasılıklar eşit olduğunda, dağılım yatay ve düz bir çizgiyle ifade edilir. Bu da grafik üzerinde dikdörtgen biçimini oluşturur.
Binom Dağılımı
Bugün yazı turayı kazandığınızı düşünelim; bu başarılı bir olaydır. Ardından tekrar yazı tura attınız, ama bu kez kaybettiniz. Bugün yazı gelmiş olması, yarın da geleceği anlamına gelmez. Şimdi, kazandığınız yazı tura sayısını temsil eden bir rastgele değişken tanımlayalım: X. Bu değişkenin alabileceği değer, attığınız yazı tura sayısına bağlı olarak herhangi bir sayı olacaktır.
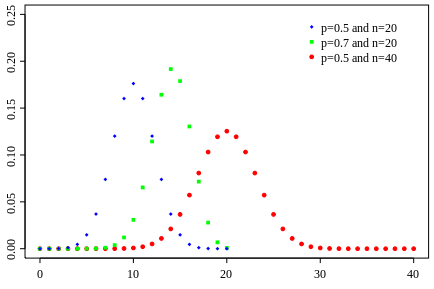
Elimizde yalnızca iki olası sonuç vardır: Yazı → başarı ve Tura → başarısızlık. Bu durumda başarı olasılığı p = 0.5 ve başarısızlık olasılığı ise q = 1 – p = 0.5 olur.
Tüm denemelerde yalnızca iki sonuç (başarı ya da başarısızlık) mümkünse ve her denemede başarı ile başarısızlık olasılığı aynıysa, bu dağılıma Binom Dağılımı denir. Binom Dağılımının temel özellikleri şunlardır:
- Her bir deneme birbirinden bağımsızdır.
- Her denemede yalnızca iki olası sonuç vardır: başarı ya da başarısızlık.
- Toplamda n adet özdeş deneme yapılır.
- Başarı ve başarısızlık olasılıkları her denemede aynıdır (yani tüm denemeler aynı yapıya sahiptir). Bu özellikler, binom dağılımını hem teoride hem uygulamada yaygın bir araç hâline getirir.
Normal Dağılım (Gauss-Laplace Dağılımı) Nedir?
Sokakta rastgele karşılaştığınız bir kadının tam olarak 170 cm boyunda olma ihtimali nedir? Soru, ilk bakışta cevapsız gibi görünse de, matematik burada devreye girer. İnsan boyları gibi biyolojik özellikler, genellikle normal dağılım adı verilen bir olasılık dağılımını takip eder. Pek çok küçük rastlantısal değişkenin toplamı, genellikle normal dağılım gösterir. Bu özellik de onun bu kadar yaygın kullanılmasını sağlar.
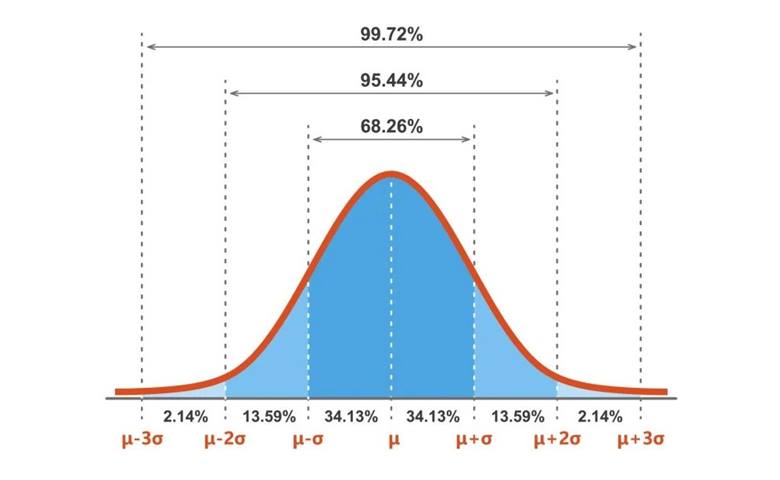
- Bir dağılımın normal dağılım olarak kabul edilebilmesi için şu özelliklere sahip olması gerekir:
- Değerlerin yarısı merkezin solunda, diğer yarısı ise sağındadır.
- Ortalama (mean), medyan (median) ve tepe değeri (mod) aynı noktadadır.
- Dağılımın eğrisi çan şeklindedir ve x = μ doğrusu etrafında simetriktir.
- Eğrinin altındaki toplam alan 1’dir, yani olasılıkların toplamı %100’dür.
Normal dağılım, yapısı bakımından binom dağılımdan oldukça farklıdır. Ancak deneme sayısı çok yüksek olduğunda (n → ∞), binom dağılımının şekli de normal dağılıma benzemeye başlar. Bu, iki dağılım arasında önemli bir bağlantıdır.
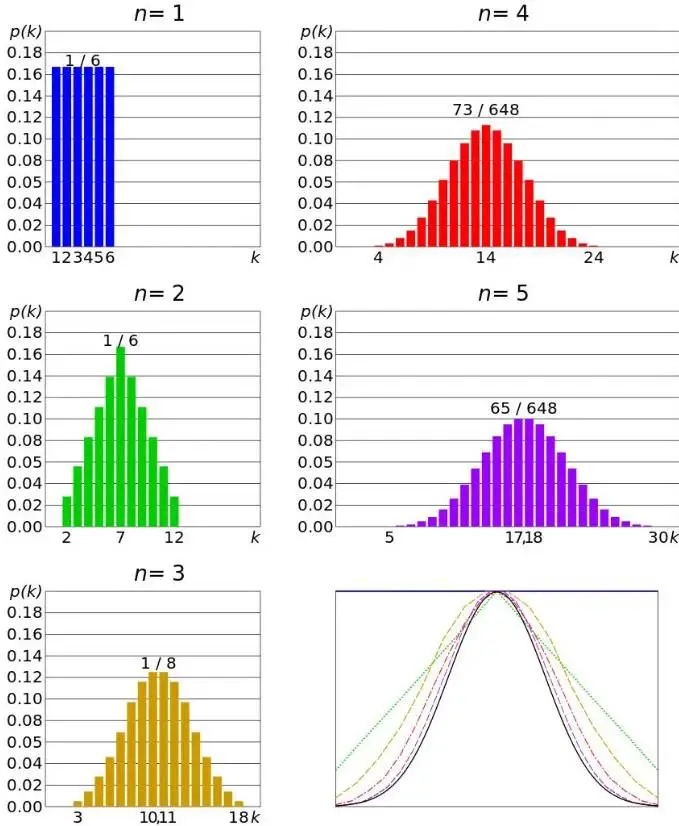
Poisson Dağılımı
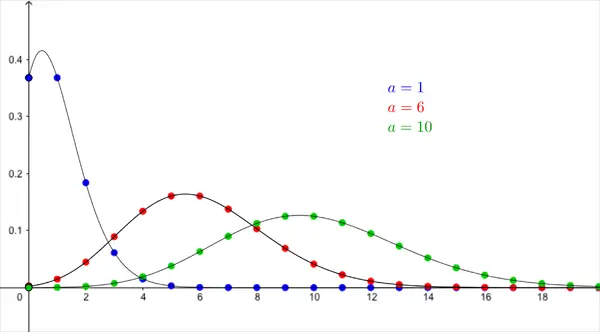
Poisson dağılımı, sabit bir zaman veya mekan aralığında meydana gelen olayların sayısını modeller. Diyelim ki bir çağrı merkezinde çalışıyorsunuz. Günde yaklaşık kaç çağrı alıyorsunuz? Bu sayı her gün değişebilir. İşte bir çağrı merkezine bir günde gelen toplam çağrı sayısı gibi durumlar, Poisson dağılımı ile modellenir. Benzer örnekler şunlardır:
- Bir hastanede bir günde kaydedilen acil çağrıların sayısı
- Belirli bir bölgede bir günde bildirilen hırsızlık olayları
- Bir kuaföre bir saat içinde gelen müşteri sayısı
- Belirli bir şehirde bir günde bildirilen intihar vakaları
- Bir kitap sayfasında oluşan baskı hatalarının sayısı
Poisson dağılımı, olayların rastgele zaman ve mekân noktalarında gerçekleştiği durumlar için uygundur. Bu tür modellerde önemli olan, olayların kaç kez gerçekleştiğidir—ne zaman gerçekleştiği değil. Bu nedenle Poisson dağılımı, olayların sıklığını saymakla ilgilenilen tüm senaryolarda kullanılır.
Log-Normal Dağılım
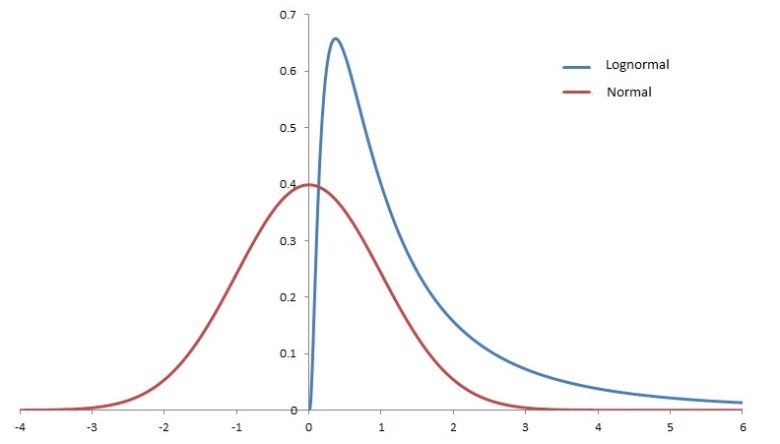
Lognormal dağılım; logaritması normal olarak dağılan bir rastgele değişkenin ayrık ve devam eden dağılımıdır. Bir başka deyişle bu dağılımda orijinal veriler normal olarak dağılmak yerine, hesaplanan bu orijinal verilerin logaritmaları normal olarak dağılır. Bu dağılım tanımı gereği sadece pozitif değerlerden oluşur. Çünkü değişkenleri ln(x1), ln(x2), ln(x3) gibi değişkenlerdir.
Lognormal dağılımının bazı yaygın kullanım alanlarına bakım veri analizlerini veya borsa veri analizlerini örnek verebiliriz. Örneğin borsada lognormal dağılım, hisse senedinin gelecekteki getirilerini tahmin etmek amacıyla kullanılmaktadır.
Sonuç Olarak
Yazımızda bu noktaya kadar karşınıza en sık çıkma ihtimali olan dağılımlardan bahsettik. Ancak daha bahsetmediğimiz onlarca dağılım olduğunu anımsatalım. Tüm bu olasılık dağılımları modern istatistiğin ve veri biliminin omurgasını oluşturur.
Kaynaklar ve ileri Okumalar:
- Maths in a minute: The normal distribution. Yayınlanma tarihi: 7 Ocak 2022; Bağlantı: Maths in a minute: The normal distribution
- Maths in a minute: The binomial distribution. Yayınlanma tarihi: 7 Ocak 2022; Bağlantı: Maths in a minute: The binomial distributionn
- Poisson Distribution; Bağlantı:https://www.sciencedirect.com/
Matematiksel





