Yazımıza bir soru ile başlayalım. “Bir fastfood restoranının her Cuma gecesi ortalama 400 müşterisi varsa, herhangi bir Cuma gecesi 600 müşterinin gelme olasılığı nedir?” Bu soru size bir miktar anlamsız gelmiş olmalıdır. Sonuçta henüz gerçekleşmemiş ve gelecekte olacak olan bir olay için belirli bir tahminde bulunmamız gerekiyor.
Bu mümkün değildir diye düşünüyorsanız aslında yanılıyorsunuz. Mevcut istatistikleri inceleyip gelecek hakkında tahminde bulunmamız aslında mümkündür. Aslına bakarsanız Poisson dağılımı geleceği okumaya cesaret eden ilk formüllerden biridir.
Poisson Dağılımı Nedir?
Adını Fransız matematikçi Siméon Denis Poisson’dan (1781 – 1840) alan bir Poisson dağılımı, bir olayın ne sıklıkta meydana geldiğini bildiğinizde, belirli olayların gerçekleşme olasılığını tahmin etmeye yardımcı olan bir araçtır.

Poisson dağılımının doğru olabilmesi için tüm olayların birbirinden bağımsız olması gerekir. Ayrıca olayların zamana göre hızlarının sabit olması ve olayların aynı anda oluşamaması gerekir. Ayrıca, ortalama ve varyans birbirine eşit olmalıdır.
“Hayat sadece iki şey için yaşamaya değer. Matematik yapmak ve matematik öğretmek” söylemi ile hatırlanan Fransız bilim tarihinin en çok eser bırakan isimlerinden birisi olan Siméon-Denis Poisson, bu dağılımı ilk olarak 1837 tarihli Recherches sur la probabilite des jugements en matière criminelle et matière civile ( Ceza hukuku ve medeni hukuk alanlarındaki hükümlerin olasılığı üzerinde araştırmalar) adlı çalışmasında ortaya atmıştır. Şimdi gelin biraz daha detaya inelim.
Poisson Dağılımı Nasıl Hesaplanır?
Belirli bir zaman diliminde bir olayın ortalama a kez gerçekleştiğini varsayalım. Örneğin, sosyal medya akışınızda dakikada ortalama üç yeni gönderi göreceğinizi biliyor olduğunuzu düşünelim. Ama dikkat ederseniz ortalama dedik. Yani bu bir dakikada kesin 3 bilgi göreceğiniz anlamına gelmez. Algoritmanın tercihine göre, bazen dakikada beş, bazen ise yalnızca 1 yeni gönderi görebilirsiniz.
Dolayısıyla, “Bir dakika içinde tam olarak k yeni gönderi görme olasılığım nedir?” diye sormakta haklısınız. Burada k, 0 veya 1 veya 2 veya başka herhangi bir pozitif tam sayı olabilir.
Bu soruyu cevaplamak için bir olasılık dağılımına ihtiyacınız var. Olasılık dağılımları, önceden emin olamayacağınız birden fazla sonucu olan süreçleri tanımlamamıza yarar. Aslına bakarsanız bir çok olasılık dağılımı vardır. Farklı olasılık dağılımları farklı amaçlara hizmet eder ve farklı veri üretim süreçlerini temsil eder. İşte bu dağılımlardan bir tanesi de Poisson dağılımıdır.
Bu dağılım söz konusu olaylar birbirinden bağımsız olduğu sürece işe yarayacaktır. Bunun sonucunda da bir olayın belirli bir birim zamanda tam olarak k kez gerçekleşme olasılığı aşağıdaki formülle hesaplanacaktır.
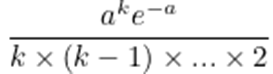
Sosyal medya örneğimizde, “a” dakikada 3 gönderiye eşittir. Gönderilerin tamamen bağımsız olduğunu varsayarsak bir dakikada tam olarak bir yeni gönderi görme olasılığınız aşağıdaki gibi olacaktır.
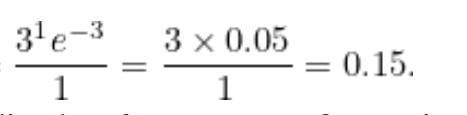
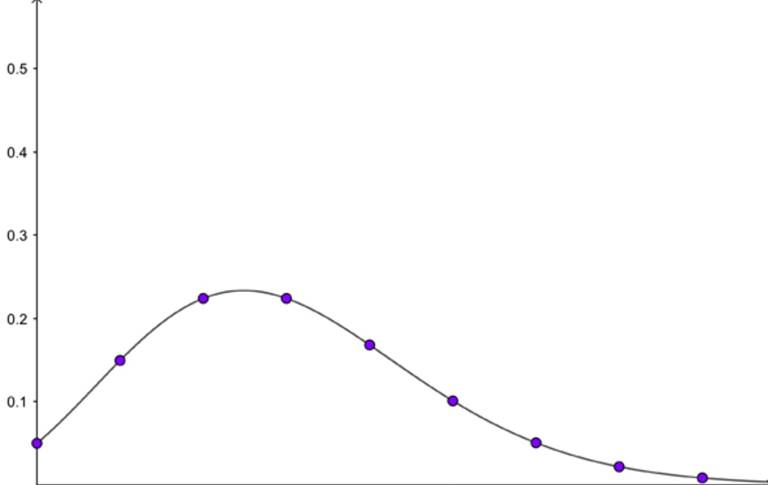
Aşağıdaki grafik a=3 için Poisson dağılımını göstermektedir. Gördüğünüz gibi k büyüdükçe, birim zamanda k olay görme olasılığı sıfır olma eğilimindedir.
Poisson Dağılımı Ne İşimize Yarayacaktır?
1837’de Fransız matematikçi Siméon Poisson tarafından tanıtılan ve Abraham de Moivre’nin çalışmasına dayanan bu dağılım yardımıyla, bir bölgede görülen tifo hastalığının sayısı, gün içerisinde eczaneye tansiyon ölçtürmeye giden kişi sayısı, bir kavşakta oluşan kaza sayısı, bir müşteri hizmetleri servisine her saat başı gelen telefon sayısı, bir duraktan saat başı geçen otobüs seferlerinin sayısı gibi çok çeşitli olasılıkları tahmin etmek mümkündür.
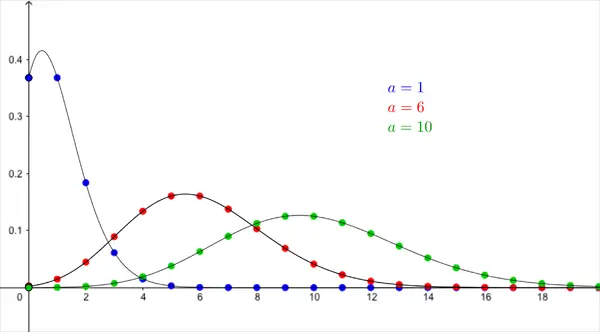
Genellikle bir Poisson dağılımı büyük sayıda olay ortaya çıkabilmesi mümkün olduğu, ama bu ortaya çıkması mümkün olayların nadir olduğu sistemlerde uygulanabilir. Bilimsel alanlarda klasik örnekler atomların nükleer parçalanması; verilen bir DNA zincirinde ortaya çıkan mutasyon sayısı gibi şeylerdir.
Şimdilik geleceği tam olarak tahmin edebilme becerisine sahip olamasak da bu sonuçları elde edebilmemiz bile önemli başarılardır.
Kaynaklar ve ileri okumalar:
- Maths in a minute: The Poisson distribution. yayınlanma tarihi: 7 Ocak 2022. Kaynak site: Plus Math. Bağlantı: Maths in a minute: The Poisson distribution/
- Poisson Distribution Formula and Meaning in Finance. Yayınlanma tarihi: 19 Mayıs 2022; Kaynak site: Investopedia. Bağlantı: Poisson Distribution Formula and Meaning in Financ/
Size Bir Mesajımız Var!
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.





