Matematikte bazı varsayımlar anlaşılması kolay ancak kanıtlanması son derece zor olanlar kategorisine girer. Buna bir örnek asal sayıların sayı doğrusu üzerine dağılımı ve ikiz asal sayılar ile ilgilidir.

Öklid’in ispatını yaptığı zamandan beri sonsuz sayıda asal sayı olduğunu biliyoruz. Ancak bu asal sayıları bulmanın kolay olduğunu düşünüyorsanız aslında yanılıyorsunuz. Asal sayılar sayı doğrusu başında bol miktarda bulunmalarına rağmen dağılımları eşit aralıklarla değildir. Sayılar büyüdükçe birbirlerinden giderek uzaklaşırlar.
Örneğin, ilk 10 sayıyı düşünürsek 2,3,5 ve 7 yani yüzde 40’ı asaldır. Ancak ilk 100 sayı içinde 25 tane asal sayı olduğunu görürüz. 1001 ile 1100 arasında yalnızca 16, 100001 ve 100100 sayıları arasında da sadece altı tane asal sayı vardır. 10 basamaklı sayıların tamamını ele aldığımızda bu sayıların yalnızca yaklaşık yüzde 4’ü asaldır.

Gördüğünüz gibi asal sayılar giderek azalır. Başka bir deyişle, ardışık iki asal sayı arasındaki mesafe giderek artar. Aslına bakarsanız iki ardışık asal sayı birbirine inanılmaz derece uzak olabilir. Diğer bir deyişle, sonsuz sayıda asal sayı vardır ve ayrıca ardışık asal sayılar birbirinden sonsuz derecede uzaktadır.
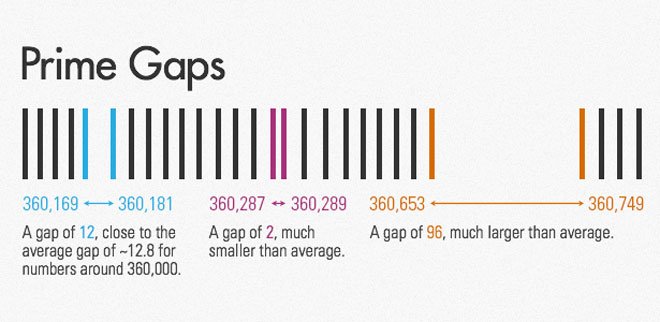
Prensip olarak bir asal sayı ile bir sonraki asal sayı arasındaki ortalama uzaklık ln(p) değeridir. Burada p = 19 sayısı için ln(19) ≈ 3’e karşılık gelir. Ancak daha büyük bir asal sayı olan 2.147.483.647 için uzaklık 22 civarındadır. Gördüğünüz gibi asal sayılar arasındaki ortalama uzaklık p büyüdükçe artar. Matematikçilerin merak ettikleri şey, asal sayılar arasındaki ortalama mesafe arttıkça, belirli bir noktadan sonra ikiz asal sayıların olup olmadığı ile ilgilidir.
İkiz Asallar Nedir?
Aralarındaki fark 2 olan ardışık asal sayılara ikiz asallar denir. Örneğin (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), (71, 73), (101, 103), (107, 109), (137, 139) çiftleri ikiz asal sayılardır. İkiz asallar varsayımı, sayılar teorisinde ifade edilmesi kolay, ancak kanıtlanması son derece zor olan problemlerden biridir.
Sayılar evrenine girdikçe asal sayılar giderek daha seyrek hale gelse de, başka bir ikiz asal çifti karşımıza çıkar. Örneğin, 1129’dan sonra, sonraki 21 sayı içinde bulamazsınız; sonra aniden 1151 ve 1153 ikiz asalları ortaya çıkar. Çok büyük ikiz asallar vardır fakat en büyüğünün ne olduğunu bilemiyoruz. Ama yine de ikiz asallardan sonsuz tane olduğunu düşünüyoruz.
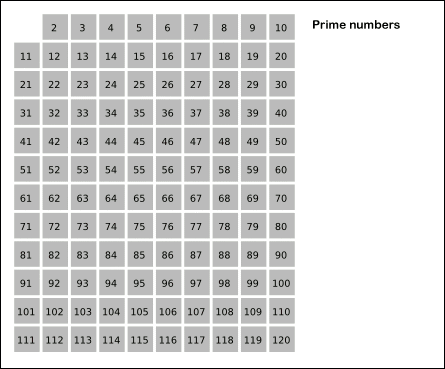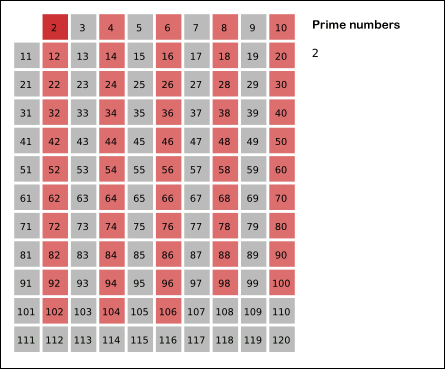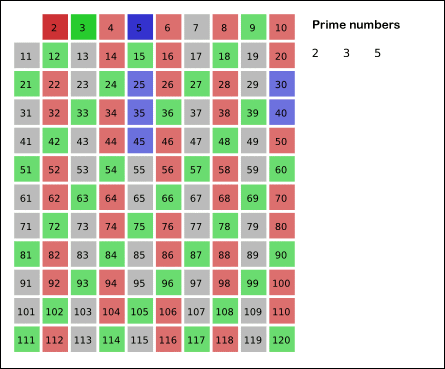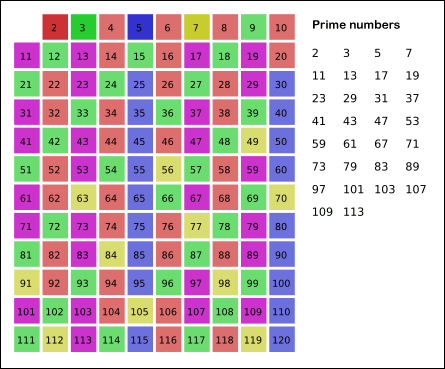
Matematikçiler 18. yüzyıldan beri asal sayıların daha küçük sayılar arasında daha yaygın olduğunu biliyor. Daha büyük sayılara baktıkça bu sayılar giderek daha nadir hale geliyor. Üstelik İkiz asal sayılar, sıradan asal sayılara göre daha da nadirdir. Bu nedenle onları bulmak da kolay değildir. ( İlk milyon tam sayı arasında yalnızca 8169 tane vardır.)
Ne Kadar İlerleme Kaydettik?
Bu konu ile ilgili bir araştırma da geçtiğimiz yıllarda bizi mutlu etmişti. Boğaziçi Üniversitesi’nden Prof. Dr. Cem Yalçın Yıldırım çalışma arkadaşları Daniel Goldston ve Janos Pintz ile birlikte sanı hakkında önemli bir gelişmeye imza atmışlardı. Çalışmaları sonsuz sayıda ikiz asal olduğunu kanıtlamasa da, bu yönde atılmış önemli bir adımdı. Bu sayede de sayılar teorisi alanında 2014 Frank Nelson Cole Ödülü – kısaca Cole ödülü – sahibi olmuşlardı.
Bu sonuçtan sonra İkiz Asallar Sanısı için umutlar arttı. Ancak aralarındaki fark 2 olan sonsuz tane asal sayı çifti bulma fikrimizden vazgeçtik. Örneğin aralarındaki fark 10’dan fazla olmayan sonsuz tane p ve q asal sayı çifti bilebilir miyiz? Yitang Zhang aralarındaki fark yetmiş milyondan fazla olmayan sonsuz tane asal sayı çifti bulunacağını gösterdi.
James Maynard, Zhang’ın yetmiş milyon olarak bulduğu sınırlamayı birdenbire 600’e indirdi. Terence Tao başkanlığında bir ekip bu sayıyı 246’ya indirdi. Ancak sonrasında ilerleme durdu. Matematikçiler problemi çözmek için tamamen yeni bir fikre ihtiyaç duyduklarını fark etmişlerdi.
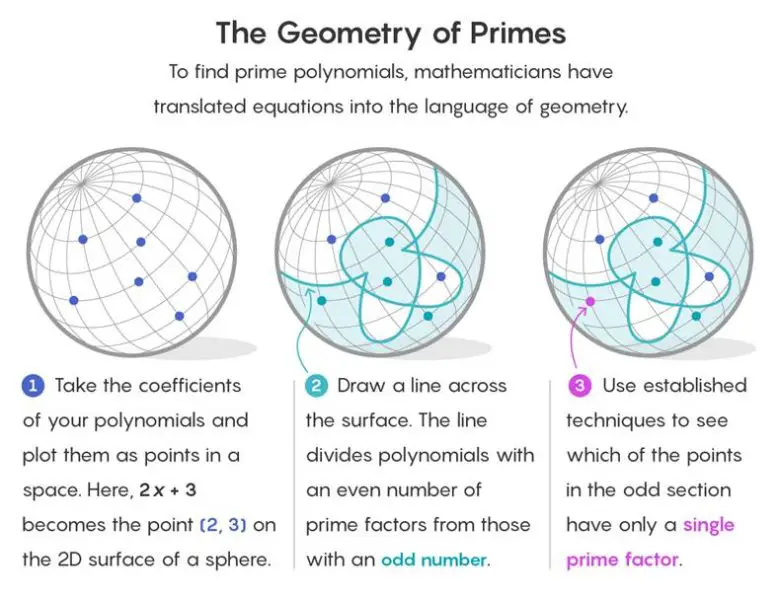
Bunun neticesinde de ikiz asalları sonlu alanlar ve asal polinomlar isimlerini verdikleri ilişkiler kapsamına aldılar. Sonrasında da ikiz asallar varsayımını, aynı Fermat’ın son teoreminin çözümünde olduğu gibi, geometri ile ilişkilendirerek çözmeye çalışmaya başladılar.
Geometrinin işin içine neden karıştığını anlamak için her polinomu uzayda bir nokta olarak hayal edin. Polinomun katsayıları, polinomun nerede bulunduğunu tanımlayan koordinatlar görevi görür. Sonuçta sonsuz sayıda polinom olduğuna göre asal sayıları polinomlar yardımı ile de incelemek olası olur. ( Daha fazla bilgi için bu yazıya göz atınız)
Sonuç olarak
Asal sayılar, profesyonellerin ve meraklıların oynayabileceği sonsuz bir matematik bulmaca dizisi oluşturur. Bunların tüm gizemlerini asla çözemeyebiliriz, ancak matematikçilerin sürekli olarak keşfedilecek yeni tür asal sayıları ortaya atacaklarına emin olabilirsiniz.
Kaynaklar ve ileri Okumalar:
- Unheralded Mathematician Bridges the Prime Gap; Yayınlanma tarihi: 19 Mayıs 2013; Bağlantı: https://www.quantamagazine.org/
- Mathematicians Solve ‘Twin Prime Conjecture’ — In an Alternate Universe; yayınlanma tarihi: 29 Ekim 2019; Kaynak site: Live Science. Bağlantı: Mathematicians Solve ‘Twin Prime Conjecture’ — In an Alternate Universe/
- Mathematical mysteries: twin primes; Yayınlanma tarihi: 1 Ocak 1998; Kaynak site: Plus Math. Bağlantı: Mathematical mysteries: twin primes/
- Berke, Allison. “An Introduction to The Twin Prime Conjecture.” (2006).
- Wong, Bertrand. (2021). The Twin Primes. 40E. 75-86. 10.5958/2320-3226.2021.00008.4.
- How Can Infinitely Many Primes Be Infinitely Far Apart? Yayınlanma tarihi: 21 Temmuz 2022. Kaynak site: Quanta Magazine. Bağlantı: How Can Infinitely Many Primes Be Infinitely Far Apart?
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel