Aradan binlerce yıl geçmesine rağmen matematikçileri pi sayısının peşini bir biçimde bırakmıyorlar. Pi’yi tipik olarak yaklaşık 3.14 olarak düşünsek de, aslında bu sayının virgülden sonra trilyonlarca basamağa sahip olduğunu biliyoruz. Aynı zamanda bu sayının son basamağını asla bulamayacağımızın da 18. yüzyıldan beri farkındayız.

Pi sayısının büyüsüne kapılan matematikçiler bazen onu görselleştirmek için de çabalar. Sonuçta da karşımıza pi sanatı diyebileceğimiz çalışmalar çıkar. Pi sayısını görselleştirme çabalarında olan matematikçilerden ilki adını kümeler kuramında sıkça andığımız John Venn’dir.
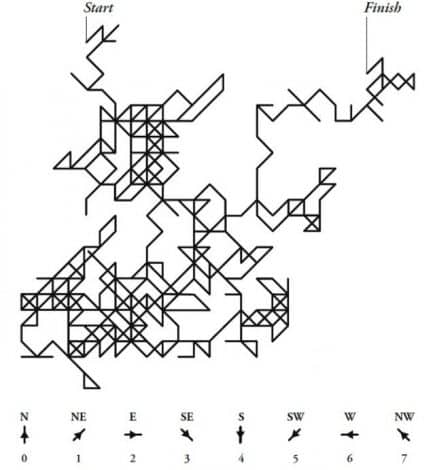
1888’de, John Venn, ilk 707 ondalık basamağı gösteren bir grafik çizerek pi’nin basamaklarının rastgele olduğunu görsel olarak göstermeye çalıştı. Bunu yapmak için 0 ile 7 arasındaki ilk 8 rakamı bir pusulanın sekiz yönü ile eşleştirdi. Ardından her bir rakamın gösterdiği yönü sadece kağıt ve kalem kullanarak çizdi. Logic of Chance adını verdiği bu çalışması sonucunda elde ettiği çizimi aşağıda görebilirsiniz.
Pi Sayısı Normal midir?
Aslında matematikçilerin Pi sayısını görselleştirme çabaları entelektüel bir arayış ile ilişkilidir. Pi sayısının ilginç bir özelliği vardır. Basamak sayısı arttıkça her rakamın görülme oranı birbirine giderek yaklaşır. Bu noktada da matematikçiler “Pi sayısı normal mi?” diye sorarlar.
Matematikçi olmayan birine bu soru garip gelebilir. Ancak aslında ilk olarak 1909’da E. Borel tarafından ortaya atılan normallik fikri, gerçek bir sayının rastgele olduğu fikrini resmileştirme girişimidir.
Pi’nin rakamlarına bakarak ve istatistiksel testler uygulayarak normal olup olmadığını belirlemeye çalışabilirsiniz. Şimdiye kadar yapılan testlerden, pi’nin normal olup olmadığı hala açık bir sorudur. Örneğin, 2003’te Yasumasa Kanada, pi’nin ilk trilyon basamağında farklı rakamların kaç kez göründüğünün dağılımını yayınladı. Aşağıdaki sonuçlar, her sayının neredeyse eşit dağıldığını ortaya koyuyor. Ancak elbette Pi sayısının tüm basamakları bilmediğimiz için bu sayının normal olacağını kanıtlamak için bu yeterli değil.

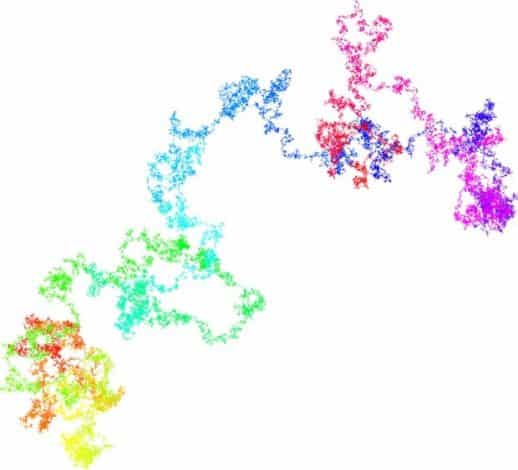
İşte bu nedenle bazı matematikçiler Pi sayısını görselleştirmeye çalışırlar. Bunlardan bir tanesi de aşağıdadır. Bu çalışmada Francisco Aragon ve meslektaşları pi’yi 4 tabanına dönüştürdü. Yani sadece 0, 1, 2 ve 3 rakamları kullanılarak yazdı. Bu rakamlar kuzey, güney, doğu ve batıyı olacak biçimde dört ana yöne atadı. 100 milyar rakamı bu biçimde düzenlediğinde elinde aşağıdaki görsel vardı.
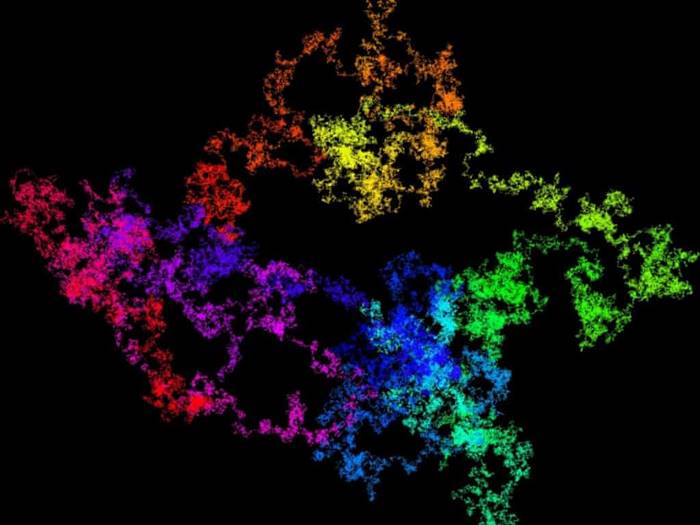
Aynı mantıkla ilk 10 milyar basamak ise aşağıdaki gibi gözükmektedir.
Daha sonra Cristian Vasile aynı fikri onluk sayı sistemimize uyguladı. Bunun için her sayının, her biri 36 derece ile ayrılmış on yönü temsil etmesine izin verdi. Sonucu aşağıda görebilirsiniz.
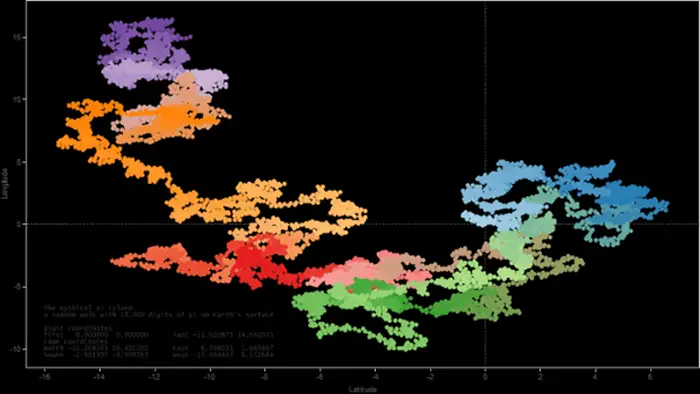
Francisco Aragon tarafından yapılan bu çalışmada da pi sayısının yine dört tabanında renklendirilmiş halini görüyorsunuz. Bir milyon karede kırmızı (0), yeşil (1), camgöbeği (2) ve mor (3) anlamına geliyor. Sonuç aşağıdaki gibi gözüküyor.

Martin Krzywinski’nin Çalışmaları
Ancak muhtemel Martin Krzywinski’nin çalışmaları diğerlerinin arasında göze daha çok hitap ettikleri için öne çıkmakta. Kendisi ilk çalışmasını 2013 yılında yaptı. Bu çalışmada her renk bir sayı ile eşleşmiş durumdadır.
Krzywinski devamında bu çalışmasını, merkezden dışa doğru genişleyen bir spiral şeklinde dizdi. Bu sefer de karşımıza başka bir görsel çıktı.
Cristian Ilies Vasile tarafından oluşturulan görüntülere dayanan Krzywinski, pi’deki rakamlar arasındaki ilişkilere dayanan bir dizi göz alıcı dairesel diyagram da derledi. Bunlardan bazılarını aşağıda görebilirsiniz.
Pi Sanatı Örnekleri
Bu çalışmada 0 ile 10 arasındaki rakamlar bir dairenin etrafına dizili durumda. Sonra da 3 ile 1, 1 ile ve 4 ve devamında pi sayısının bütün basamakları çizgiler ile birleştirilmiş.
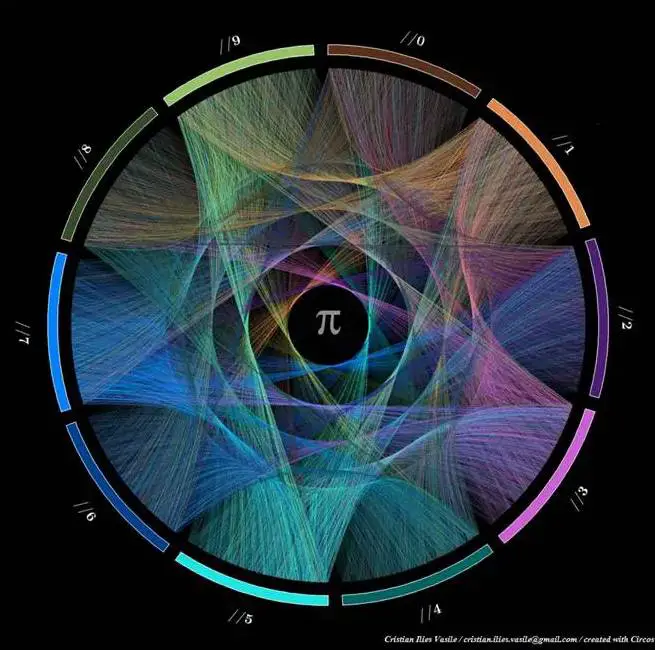
Bu çalışmanın bir başka versiyonunu da aşağıda görüyorsunuz. Bu sefer çizgiler yerine noktalar var. Bir sayı ne kadar çok tekrar ederse o kadar büyük bir nokta ile temsil ediliyor. Burada dikkat edilmesi gereken bir nokta var. En yukarıda duran mor renkli büyük nokta. Bu noktada 6 tane 9 rakamı arka arkaya geliyor. Bu durum pi sayısının 762. basamağında karşımıza çıkıyor. Bu nokta fizikçi Feynman’in bir sözüne ithaf edilerek Feynman noktası olarak anılıyor.

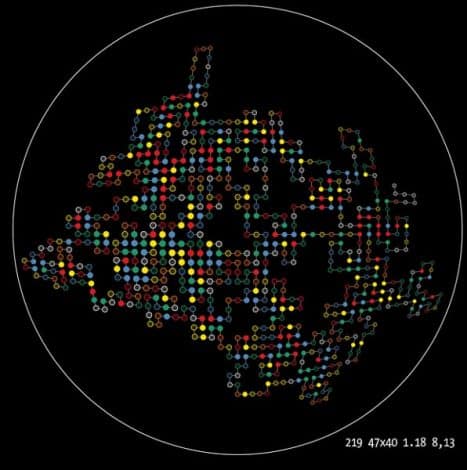
Örnek olarak göstereceğimiz bu son çalışmada da Krzywinski pi sayının 768 basamağını bir protein amino asit zinciri biçiminde şekillendirmiş. Bunun için asal sayıları (2, 3, 5 ve 7) siyah nokta ile göstermiş, diğer sayıları da renklendirmiş. Ardından bilgisayarda bir algoritma yardımıyla şekli bir çemberin içine sığdırmış.
Pi sanatı diyebileceğimiz yazımıza eklediğimiz çalışmalar buzdağının sadece görünen yüzü. Sizler de ilginç bir fikri pi sayısının basamaklarına uygulayarak kendi sanat eserinizi yapmaya çalışabilirsiniz. Fikir için de adını verdiğimiz sanatçılarının internetteki diğer çalışmalarına göz atabilirsiniz. Şimdiden iyi eğlenceler. Ayrıca göz atmak isterseniz: Binlerce Yıldır Dünyayı Büyüleyen Pi Sayısı Hakkında Bazı İlginç Bilgiler
Kaynaklar ve ileri okumalar
- Pi might look random but it’s full of hidden patterns; Yayınlanma tarihi: 14 Mart 2016; Bağlantı: https://theconversation.com/
- You’ve Never Seen Pi Like This; yayınlanma tarihi:2 Ekim 2013; Bağlantı: https://www.popsci.com/article/science/youve-never-seen-pi-0/
- Pi Day: pi transformed into incredible art – in pictures; Yayınlanma tarihi: 14 Mart 2014; Bağlantı: https://www.theguardian.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel