Bu yazıda, Pisagorcuları bile rahatsız eden irrasyonel sayıların tuhaflığını ve onlara gerçekten ihtiyacımız olup olmadığını inceleyeceğiz. Bu arada da çeşitli sayı kümeleri üzerinde düşünme fırsatımız olacak. Böylece sayı kümelerinin derin yapısı üzerinde bir fikrimiz oluşacak.
Şimdi gelin bir deney yapalım. Sayı kümelerini daha iyi anlamamızı sağlamak için tasarlanmış zihinsel bir deney. Sayı doğrusunun bir tarafına bir ışık kaynağı koyup diğer taraftan bakarsak, ne görürüz?

Durun bir saniye! Böyle soru mu olur? Ne demek ‘ne görürüz’? Elbette sayı doğrusunu görürüz! Peki ama diğer taraftaki ışık kaynağını da görebilir miyiz? Sayı doğrusunun noktalarını ışık geçirmeyen minik boncuklar olarak düşünelim. Şimdi, elimizde her noktası doldurulmuş bir doğru olacaktır. Işık kaynağını da noktasal bir güneş gibi düşünelim, yani her yönde ve her doğrultuda sonsuz miktarda ışın yayan bir kaynak olarak…
Bu durumda ışık kaynağını görmememiz gerekir, çünkü kaynaktan çıkan bütün ışınlar sayı doğrusunu dolduran sonsuz sayıda ve sonsuz yoğunlukta nokta tarafından engellenecektir. Buraya kadar ilginç bir şey söylemedik. Asıl ilginçlik şimdi başlıyor. Bu kez sayı doğrusundan İrrasyonel Sayıları çıkaralım. Geriye sadece Rasyonel Sayılar kalsın. (Yani tüm kesirler kalıyor ama pi gibi irrasyonellerin hepsini çıkarıyoruz. Onların yerine boşluklar kalsın.) Işık kaynağını yine görür müyüz?
Rasyonel Sayılar kümesi yoğun bir kümedir
Unutmayın ki Rasyonel Sayılar kümesi yoğun bir kümedir; yani birbirine ne kadar yakın olursa olsun, iki kesir arasında sonsuz sayıda kesir vardır. Örneğin: ½ ile ¼ arasında sonsuz sayıda kesir vardır. Buna karşın Rasyonel Sayılar kümesi sayı doğrusunu tam olarak doldurmayacak, arada boşluklar kalacaktır. (O boşluklara İrrasyonel Sayılar diyoruz.)

O boş noktalardan ışık sızacağı için alttaki ışık kaynağını görebileceğiz. Ama ne kadarını görebiliriz? En azından ışık kaynağının parlaklığını biraz yitirmesini bekleriz, öyle değil mi? Ne de olsa ışınların önemli bir kısmı (sonsuz sayıda kısmı) rasyonel sayıların doldurduğu boncuklara çarpıyor ve bizim gözümüze ulaşmıyor.
O halde güneş gözlüğüyle bakıyormuşuz gibi, ışık kaynağını gerçek parlaklığında görmemiz mümkün olmamalı. Ne yazık ki öyle olmuyor! Eğer bu deneyi gerçekten yapabilseydik, ışık kaynağının parlaklığından hiçbir şey yitirmediğini görecektik. Sanki sonsuz sayıda boncuğu (Rasyonel Sayıları) oraya hiç yerleştirmemişiz gibi…

Tuhaf olsa da gerçek bu. Nedeni ise çok basit. Çıkardığımız İrrasyonel Sayıların sayısı, Rasyonel Sayıların sayısından kıyaslanamayacak derecede çoktur!
İki tür sonsuzluk vardır
Evet, yanlış duymadınız. İki tür sonsuzluk var ve biri diğerinden çok daha büyük. Hatta küçük olan sonsuzluk, büyük olanın yanında esamesi bile okunmayacak kadar küçük kalıyor. Bütün bunları keşfeden matematikçinin adı George Cantor. 1845 –1918 yılları arasında yaşamış olan Cantor, modern küme kuramının temellerini atmıştır.
Cantor, Gerçek Sayılar kümesinin kardinalitesinin; Rasyonel Sayılar kümesinin kardinalitesinden çok daha büyük olduğunu göstermişti. Kardinaliteyi bir kümenin büyüklüğü (eleman sayısı) olarak düşünebilirsiniz. Cantor’dan önce bu iki kümenin eşit büyüklükte olduğu düşünülüyordu. (Ne de olsa tüm sonsuzlar eşit olmalıydı.) Ama Cantor böyle olmadığını, sonsuz kümelerin kardinalitelerinin birbirinden farklı olduğunu gösterdi. Yani her sonsuz eşit değildi, bazıları daha sonsuzdu!
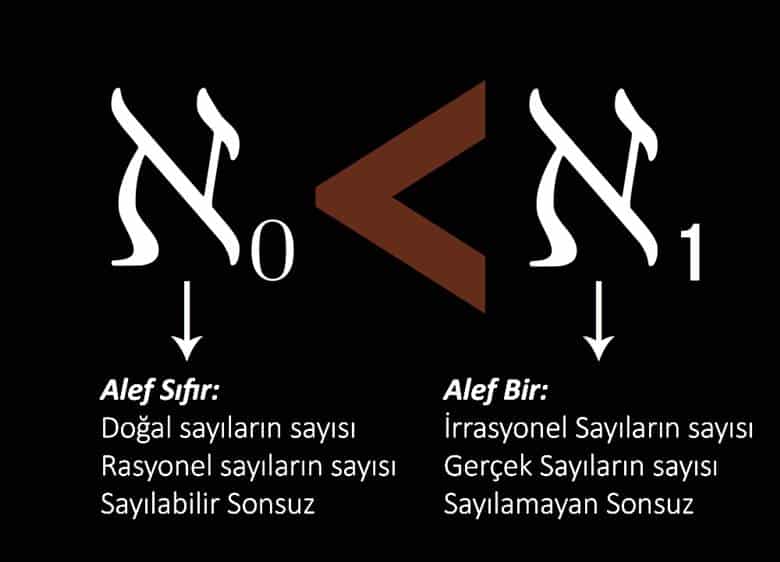
Cantor, iki tür sonsuz keşfetti. Bunlardan daha küçük olanına Alef-0 adını verdi; büyük olanına ise Alef-1. Henüz Alef-0 ile Alef-1 arasında üçüncü bir kardinalite (sonsuzluk) olup olmadığını bilmiyoruz. Ama şunu çok iyi biliyoruz ki Alef-1, Alef-0’dan çok daha büyüktür.
Gerçek Sayılar Kümesi Neden Bu Kadar Büyük?
Gerçek Sayılar kümesi, Rasyonel Sayılar kümesini içermektedir. Rasyonel Sayılar kümesinin kardinalitesinin o kadar da büyük olmadığını gördük. O halde, Gerçek Sayılar kümesini bunca büyüten ne? Aslında cevabı en başta verdik. Sayı doğrusundan irrasyonelleri çıkarırsak, alttaki ışık kaynağını nasıl göreceğimizi sormuştuk ve cevap olarak da parlaklıkta bir değişme olmayacağını belirtmiştik. İrrasyonel Sayıların bıraktığı boşluklardan ışık geçebiliyordu.
Ve şimdi biliyoruz ki İrrasyonellerin sayısı, Rasyonellerin sayısından kıyaslanamayacak derecede fazladır. Yani İrrasyonel Sayıları sayı doğrusundan çıkardığımızda geriye kalan boşluklar o kadar fazla olur ki, kaynaktan çıkan ışınlar önlerinde hiçbir engel yokmuş gibi karşı tarafa geçerler. İrrasyonel Sayılar kümesi öylesine büyük bir küme ki, Rasyonel Sayılar kümesi onun yanında hiç kalıyor.
Pisagorcular bu gerçeğe günümüzden 2500 yıl önce epeyce yaklaşmışlardı. Sayıların büyük çoğunluğunu irrasyonellerin oluşturduğunu bilemezlerdi ama kesir olmayan sayıların var olduğunu keşfetmişlerdi. Üstelik de burnumuzun dibindelerdi.
Örneğin, ikinin karekökü böyle bir sayıydı. Yani a/b = √2 olacak şekilde iki a ve b tam sayısı bulunamıyordu. Bir başka deyişle √2 sayısı iki tamsayının oranı biçiminde ifade edilemiyordu. Bu keşif onları öylesine rahatsız etti ki bu sayının varlığını inkâr ettiler ve bu bilgiyi sır olarak sakladılar. Hatta bu sırrı ifşa eden bir arkadaşlarını gemiden atarak öldürdükleri söylenir.
Kaynaklar ve ileri okumalar:
- A Brief History of Infinitesimals. The Idea That Gave Birth to Modern Calculus; Yayınlanma tarihi: 1 Nisan 2014; Bağlantı: https://www.scientificamerican.com/
- E. W. Weisstein. Irrational Number. Alındığı Tarih: 2 Kasım 2021. Bağlantı: https://mathworld.wolfram.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










