Clay Matematik Enstitüsü, çözülmemiş yedi matematik probleminin her birine 1 milyon dolarlık ödül koyduğunda, problemlerden bir tanesini küçümsemiş olabilir. Eğer matematikçiler bilgisayar biliminin “P’ye karşı NP” sorusunu doğru şekilde çözebilirse, çözümün karşılığında elde edeceklere ödül 1 milyon dolardan çok daha fazlası olacaktır. Peki P ve NP tam olarak nedir?

Konunun detaylarına geçmeden önce size basit bir soru soralım. Diyelim ki Amerika’da eğitim gören çok sayıda arkadaşınız var. Siz de uçak bileti parasını ayarladınız ve yanlarına gitmeye karar verdiniz. Sonuçta eliniz boş gitmek istemeyeceksiniz. Bu durumda hepsine hediye almanız gerekiyor. Ancak ufak bir sorununuz var. Tüm bu hediyeleri valizinize sığdırmanız mümkün değil.
Sonucunda arkadaşlarınızın kesin seveceğine inandığınız ancak havayolunun koyduğu ağırlık sınırını aşmayan bir hediye kombinasyonunu yanınıza almaya karar veriyorsunuz. Peki ama bu seçimi nasıl yapacaksınız?
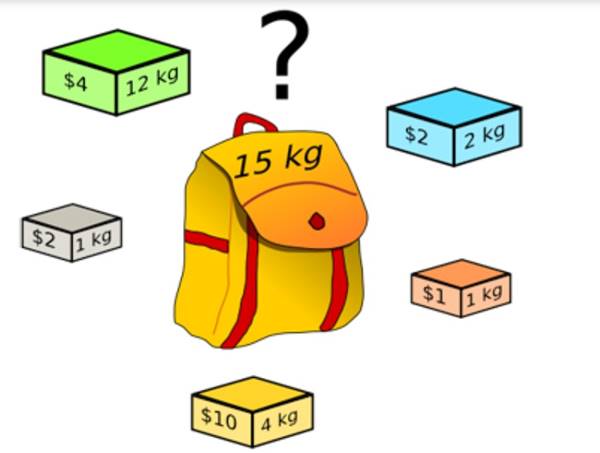
Akla gelen ilk çözüm olası tüm kombinasyonları denemek olacaktır. Ziyaret edeceğiniz arkadaş sayısı sınırlı ise kesinlikle bunu deneyin. Ancak çok çok fazla arkadaşınız var ise bu çözüm pek de pratik olmayacaktır. Bu durumda bir algoritmaya ihtiyaç duyarsınız. Bu sayede bilgisayarda gerekli tüm kombinasyonları kolayca deneyebilirsiniz.
P ile NP Nedir?
Bilgisayarlar algoritmalarla çalışır. Ancak bazı algoritmaları gerçekleştirmek sadece mikro saniyeler alırken, bazılarını gerçekleştirmek bugünkü hızla bile milyarlarca yıl alır. Burada kilit fikir, bir algoritmanın verimliliğidir. Bunu belirleyebilmek için bilgisayar biliminde karmaşıklık teorisi adı verilen bir alan vardır. Bu alanda çalışan araştırmacılar, bilgisayarların çeşitli türdeki problemleri ne kadar kolay çözebileceğini belirlemeye çalışırlar.

P, elektronik tablodaki bir sayı sütununu sıralamak veya haritada iki adres arasındaki en kısa yolu bulmak gibi verimli bir şekilde çözebilecekleri problem sınıfını temsil eder. Yani bilgisayarlar bu tür problemleri kolayca halleder. Bu algoritmalar da verimli algoritmalardır. Verilen iki sayının en küçük ortak katını bulma, bir sayının asal olup olmadığını saptama, dört işlem aritmetik hesapları P sınıfındaki problemlerdir.
Ancak aynı şey yazının başında verdiğimiz örnek için geçerli değildir. Sırt çantası problemi NP olarak kabul edilmektedir. NP, bilgisayarların çözümleri verimli bir şekilde doğrulayabildiği problem sınıfını temsil eder. NP’nin aslında bir alt küme olarak P içerdiğine dikkat edin, çünkü bir sorunu doğrudan çözmek, çözümü doğrulamanın bir yoludur.
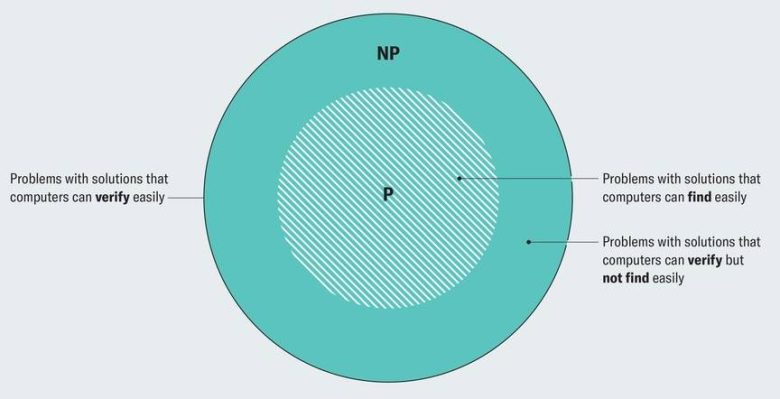
Örneğin 27 × 89 = 2403 olduğunu nasıl doğrularsınız? Çarpma işlemini kendiniz çözer ve cevabınızın iddia edilen cevapla eşleşip eşleşmediğini kontrol edersiniz. Aslında P ve NP arasındaki ilişkiyi yukarıdaki Venn şeması ile de kolayca görebiliriz.
P sınıfındaki problemlerin kolay olduğu düşünülür. Sonucunda bir bilgisayar algoritması bunları uygun bir sürede çözecektir. Ancak NP sınıfındaki problemlerin genellikle daha zor olduğu düşünülür. Sonucunda çözüm bir bilgisayar için bile milyarlarca yıl zaman alabilir.
“P = NP” Sorusu Nedir?
Yukarıdaki Venn şemasında da görebildiğiniz, NP’nin içindeki ancak P’nin içinde olmayan bölge, bilinen herhangi bir etkili algoritmayla çözülemeyen problemleri içerir. Ancak bunun, bu tür algoritmaların var olmamasından mı yoksa sadece nasıl yapacağımızı bilmemekten mi kaynaklandığını bilmiyoruz.
Bir algoritmanın bir problemi çözüyor olarak nitelendirilebilmesi için, çok büyük olanlar da dahil olmak üzere tüm örnekler için kesin bir çözüm bulması gerekir. Tüm çözümsüz gibi gözüken problemler deneme yanılma mantığı ile çözülmeye çalışılabilir. Ancak bu çok büyük bir zaman kaybı demektir. Dünyanın en hızlı süper bilgisayarlarının bile katlanarak büyümeye karşı hiçbir umudu yoktur.
Sadece bu kadar da değil. Karmaşıklığında kendi içinde de bir sıralaması vardır. NP tam ( complete) problemleri, NP’deki en zor problemler olarak kabul edilmektedir. En az her bir NP problem kadar zor olan problemlerin bulunduğu sınıfa NP-Zor (NP-hard) denir. Ve aslında bunların hepsi eşdeğerdir. Bu nedenle bir tanesini çözmeyi başarırsanız aslında hepsini çözmüş olursunuz.
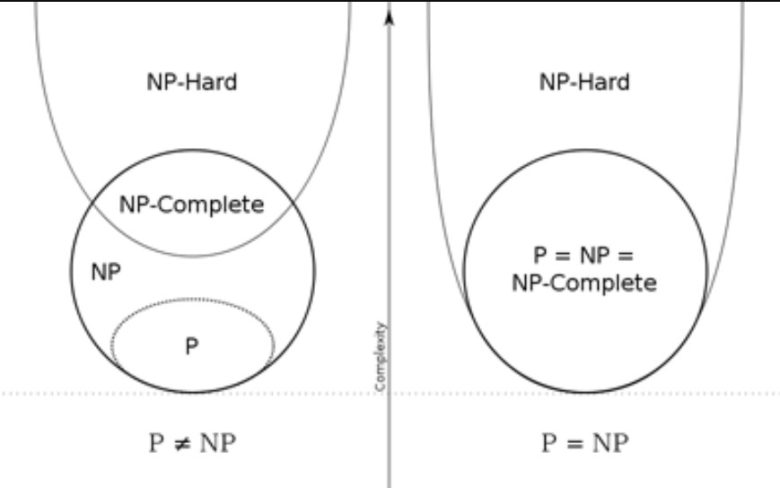
P ile NP Birbirine Eşit Olursa Ne Olur?
Hücre biyolojisinden oyun teorisine kadar, P’ye karşı NP sorusu bir çok bilim dalı ve endüstriyi ilgilendiriyor. Eğer P = NP ise (yani Venn diyagramımız tek bir daireye dönüşür ve bu zor görünen problemler için hızlı algoritmalar elde edebilirsek) o zaman tüm dijital ekonomi çökmeye karşı savunmasız hale gelir.
Bunun nedeni, kredi kartı numaranız ve şifreleriniz gibi şeyleri güvence altına alan kriptografinin yalnızca gizli anahtarı bildiğiniz takdirde çözülmesi kolay olabilecek, hesaplama açısından zor problemleri temel alarak çalışmasıdır.

P ile NP probleminden bahsedildiği zamanlarda akla ilk olarak en ünlü örnek olarak Gezgin Satıcı problemi gelecektir. Aralarındaki mesafeyi bildiğiniz, ziyaret edilmesi gereken bir sürü yeri olan, ve her yeri tam olarak bir kez ziyaret ettikten sonra, en sonunda başa dönmeniz gereken her durumda en kısa rotayı bulmanız gezgin satıcı problemi ile ilgilidir. Az sayıda yer varsa, tüm olası rotalara bakarak cevabı kolayca bulabilirsiniz. Ancak gidilmesi gereken yer sayısı arttıkça, bu hesaplama inanılmaz derecede sıkıcı hale gelir.
Sonuç olarak
Gördüğünüz gibi bu problem yazıdaki sırt çantası problemi ile eşdeğer mantıktadır. Bu yüzden biri çözülürse diğerleri de çözülecektir.
Gezgin satıcı problemi için bir algoritma bulduğunuzu hayal edin. Bu, NP’deki her problemin çözülebileceği anlamına da gelir. Sonuç olarak P=NP’yi kanıtlamış olursunuz ve gidip 1 milyon dolarınızı alabilirdiniz. Ancak alacağınız ödülün yanında bunun başka anlamları da olurdu. Bu arada endişelendiyseniz güzel haber. Çoğu uzman P’nin NP’ye eşit olmadığına inanmaktadır.
Kaynaklar ve ileri okumalar:
- An extremely superficial look at some complexity classes. Yayınlanma tarihi: 25 Ocak 2018; Bağlantı: An extremely superficial look at some complexity classes
- P vs. NP – The Greatest Unsolved Problem in Computer Science. Kaynak site: Quanta Magazine. Bağlantı: P vs. NP – The Greatest Unsolved Problem in Computer Science
- Maths in a minute: The knapsack problem. Yayınlanma tarihi: 13 Nisan 2017; Bağlantı: Maths in a minute: The knapsack problem
- The Most Important Unsolved Problem in Computer Science. Yayınlanma tarihi: 22 Aralık 2023. Bağlantı: The Most Important Unsolved Problem in Computer Science
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel