Denklem çözme konusunda sıkıntı yaşamıyor olabilirsiniz. Ancak emin olun gördüğünüz zaman nasıl çözeceğiniz konusunda pek de bir fikrinizin olmayacağı bir çok denklem vardır. Aslında bilim insanlarının karşısına çıkan denklemlerin çoğu da bu biçimdedir. Bu tip zorlu denklemler karşısında farklı yaklaşımlara ihtiyaç duyulacaktır. Bunlardan birisi de bisecting yani ikiye bölme – yarılama metodu olacaktır.
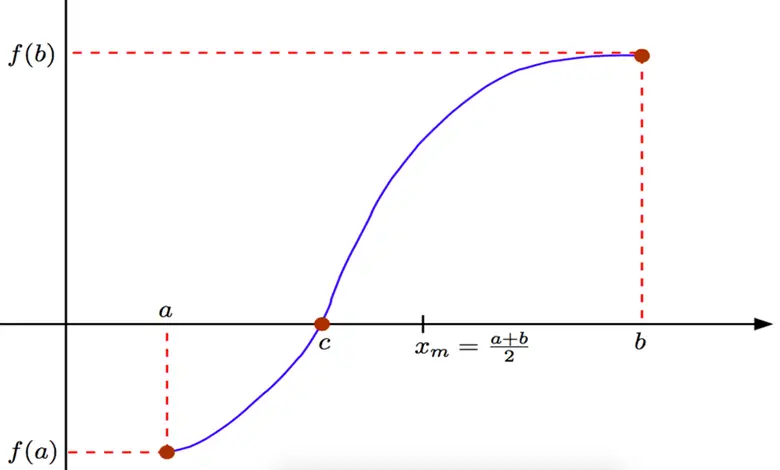
Ancak öncelikle konuya yabancı olanlar için bazı önbilgiler verelim. Bir denklemi çözmek demek denklemin kök ya da köklerini bulmak anlamına gelir. Bir denklemin kökleri f(x) = 0’ın çözümleridir. Bu aynı zamanda, f(x) fonksiyonunun grafiğinin x eksenini kestiği yerdir. Eğer fonksiyon bir aralıkta sürekli ise yani elinizi kaldırmadan fonksiyonun grafiğini çizebiliyorsanız ve fonksiyonun işareti bu aralıkta değişiyorsa, bu fonksiyon muhakkak f(x)=0 noktasından geçiyordur ve x değeri de bu fonksiyonun bir köküdür.
İkiye Bölme Metodu Nedir?
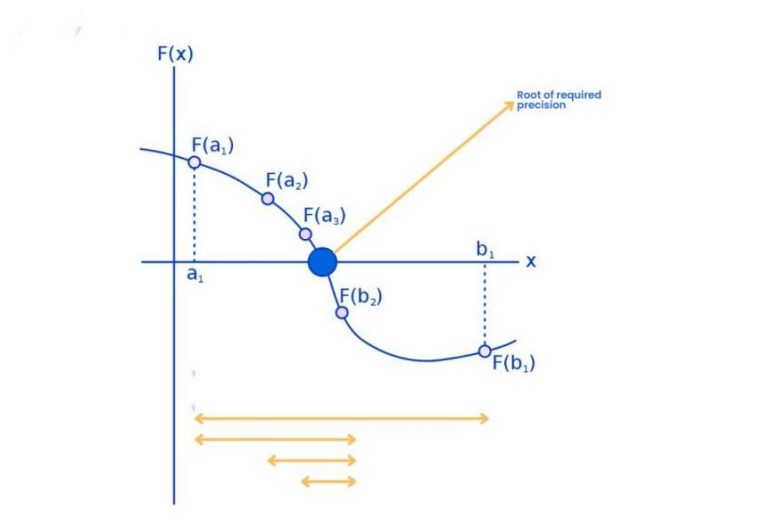
Şimdi elimizde bir f sürekli bir fonksiyonu olsun. Ayrıca bu fonksiyonun tanımlı olduğu [a,b] aralığında, f(a) ve f(b)’nin zıt işaretlere sahip olduğunu bilelim. Bundan sonrasında yapmamız gereken şey oldukça basit. İşlemimiz sadece iki sayının ortasındaki sayıyı bulmak, bunun için de aritmetik ortalama almak olacak. Yani basitçe söylemek gerekirse sayıları toplayıp sonra da ikiye bölerek yeni bir nokta ( c diyelim) elde edeceğiz. Bu c noktası ( a+b)/2 ile bulunacak.
Bu işlemin sonucunda ya f(a) ve f(c) ya da f(c) ve f(b) zıt işaretlere sahip olacaktır. Bu durumda hangisinin zıt işarete sahip olduğunu belirleyerek aradığımız kökü yaklaşık olarak bulmak için yukarıdaki adımları bir kere daha uygulamamız gerekecektir. Eğer f(a) ve f(c) zıt işaretlere sahipse b’nin değeri c ile değiştirilmelidir. Eğer f(b) ve f(c) zıt işaretlere sahipse bu sefer a’nın değeri c ile değiştirilir. Son olarak f(c)=0 olması durumunda da çözüm olarak c alınır ve süreç tamamlanır.
İkiye Bölme Metodu İle İlgili Bir Örnek
Soru: f(x)=x^{3}-x-2 \: denkleminin \: köklerini \: x\in[1,2]\, için\, bulunuzŞimdi yukarıdaki soruyu ikiye bölme metodu ile çözmeye çalışalım. Öncelikle a=1 ve b=2 değerlerini alıp yerlerine koyalım. Bu durumda f(1)=-2 ve f(2)=4 sonuçlarını elde ederiz. Ayrıca fonksiyonun sürekli bir fonksiyon olduğunu biliyoruz. Bu nedenle aradığımız cevap [1,2] aralığında bir değer olmalı. Şimdi 1. adım olarak a=1 ve b=2 değerlerinin ortasındaki değeri bulalım. Yani 1 ile 2’yi toplayıp sonrasında ikiye bölelim. Bu durumda ilk c’miz 1,5 olacaktır. Sonrasında da bu bulduğumuz değeri fonksiyonda yerine yazarsak f(c)=−0.125 olacaktır. Bulduğumuz f(c) negatif bir sonuca sahip olduğu için a’nın değeri c ile değiştirilmeli.
Aynı mantığa devam ederek aşağıda gördüğünüz tabloyu oluşturabiliriz. Tabloyu dikkatli incelerseniz 13. adımdan sonra 13 yinelemeden sonra fonksiyonun 1,521’e yakınsadığını görebilirsiniz. Bu durumda aradığımız fonksiyonun kökü 1,521 civarında olacaktır.
| Adım Sayısı | a | b | c | f(c) |
| 1 | 1 | 2 | 1,5 | −0.125 |
| 2 | 1,5 | 2 | 1,75 | 1.6093750 |
| 3 | 1,5 | 1,75 | 1.625 | 0.6660156 |
| 4 | 1,5 | 1.625 | 1.5625 | 0.2521973 |
| 5 | 1,5 | 1.5625 | 1.5312500 | 0.0591125 |
| 6 | 1,5 | 1.5312500 | 1.5156250 | −0.0340538 |
| 7 | 1.5156250 | 1.5312500 | 1.5234375 | 0.0122504 |
| 8 | 1.5156250 | 1.5234375 | 1.5195313 | −0.0109712 |
| 9 | 1.5195313 | 1.5234375 | 1.5214844 | 0.0006222 |
| 10 | 1.5195313 | 1.5214844 | 1.5205078 | −0.0051789 |
| 11 | 1.5205078 | 1.5214844 | 1.5209961 | −0.0022794 |
| 12 | 1.5209961 | 1.5214844 | 1.5212402 | −0.0008289 |
| 13 | 1.5212402 | 1.5214844 | 1.5213623 | −0.0001034 |
| 14 | 1.5213623 | 1.5214844 | 1.5214233 | 0.0002594 |
| 15 | 1.5213623 | 1.5214233 | 1.5213928 | 0.0000780 |
İkiye Bölme Metodu Ne Zaman Kullanılmalıdır?
Yukarıda size kısaca açıklamaya çalıştığımız yöntemin bazı avantajları ve dezavantajları vardır. Öncelikle gördüğünüz gibi ikiye bölme yöntemi sayesinde bir denklemin kökünü yaklaşık olarak bulsak bile hassas bir cevap elde etmek istiyorsak adımları bir çok kez tekrar etmemiz gerekiyor. (Bunu yapan şey bir bilgisayar olduğunda bu çok da sorun olmayacaktır). Ancak bu yöntemde fonksiyonunun belli bir sayıya yakınsaması garantilidir.
Bu yöntem ile her fonksiyonun kökünü bulamazsınız. Sürekli olmayan fonksiyonlarda bu yöntemi kullanmak olası değildir. Ancak olası hataları kontrol etmek olası olasıdır ve bu yarılama yöntemini bir algoritma haline getirmek kolaydır. ( Merak ederseniz kaynaklarda ilgili algoritmayı bulabilirsiniz.) Bu nedenle yöntem günümüzde hesaplamalı bilimlerde aktif olarak kullanılmaktadır. Denemek isteyebilirsiniz.
Yazının devamında ayrıca göz atmak isterseniz. Matematik İspatlarıyla Bilgisayar Programlarını Birleştiren Derin Bağlantı: Curry-Howard Yazışması Nedir?
Kaynaklar ve ileri okumalar
- Bisection Method: Definition, Procedure, and Solved Examples. Yayınlanma tarihi: 7 Temmuz 2023. Bağlantı: Bisection Method: Definition, Procedure, and Solved Examples
- Bisection Method: Bağlantı: https://protonstalk.com/polynomials/bisection-method/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel






