Olasılıklar arasında mümkün olan en iyi rotayı bulma problemi matematikçiler tarafından Gezgin Satıcı problemi olarak bilinir
Sabah uyandınız ve o gün içinde yapmanız gereken bir çok iş olduğunu fark ettiniz diyelim. Bankaya uğramalısınız, alışveriş yapmalısınız, çocukları okuldan almalısınız, en son olarak da doktora uğrayıp reçete yazdırmalısınız.
Bunları halletmek için bir arabaya sahip olabilirsiniz ancak benzin fiyatları ortada. Bu durumda araba sürmeniz gereken mesafenin mümkün olduğunca kısa olması için bunları hangi sırayla yapmalısınız? Matematik ne işe yarar diyenlere bu giriş bir hatırlatma olsun. Çünkü yukarıda aktardığımız senaryo matematikçilerin uzun zamandır üzerinde çalışmalar yaptığı gezgin satıcı problemi ile ilgilidir.
Az sayıda uğramanız gereken durak için problemi çözmek zor değildir. Ancak durak sayısı arttıkça çözmek neredeyse kesinlikle bir kuantum bilgisayarı gerektirecektir. Bu tür problemleri çözmenin en basit yaklaşımı “kaba kuvvet yaklaşımı” dediğimiz şeyi kullanmaktır.
Kaba kuvvet yaklaşımı ile olası her yolun mesafesini hesaplar ve hangisinin en kısa olduğunu belirleyebilirsiniz. Ancak olası sonuçlarının sayısının çok hızlı arttığını düşünürsek gezgin satıcı problemini bu biçimde çözmenin bir yolu yoktur.
Toplamda herhangi bir sayıda varış noktası için, buna N diyelim, olası tur sayısı ( N -1)!/2’dir. Sadece 5 yer uğrayacağınızı düşünürsek 12 olası rota ortaya çıkacaktır ve en kısa olanın hesaplanması bilgisayar olmadan bile kolaydır.
Modern bilgisayarın bir turu hesaplaması yaklaşık bir mikrosaniye sürer. Ancak 10 varış noktası için 181.400 benzersiz yol vardır. Bir bilgisayar bunu neredeyse tam bir saniyede hesaplar. 15 varış noktası için hesaplama yaklaşık yarım gün ve 20 varış noktası için yaklaşık 2.000 yıl sürer.
25 varış noktasına ulaştığınızda, yolunuzu optimize etmek için bilgisayarınızı yaklaşık 10 milyar yıl çalıştırmanız gerekir. Neyse ki, hesaplama açısından zor birçok problem kuantum bilgisayar kullanılarak çok daha kısa sürede hesaplanabilir.
Gezgin Satıcı Problemi Nedir?
Bulunduğu noktadan başlayarak, belirli sayıda noktaya birer defa uğrayan, sonunda başladığı noktaya dönen ve bu güzergâh boyunca kat ettiği toplam mesafeyi en az kısa tutmak isteyen bir gezginin uğrayacağı noktaların sırasının belirlenmesi problemi gezgin satıcı problemi olarak tanımlanır.
Lojistik faaliyetlerinde, ürünlerin dağıtımında, uğranması gereken boşaltım noktalarının sırasına karar verirken karşılaşılan bir çok problem, bir çeşit gezgin satıcı problemi gibi düşünülebilir. Bu problemin, basitliğine rağmen, aslında çok sayıda pratik uygulaması vardır.
Diyelim ki çok sayıda şehre uçmanız gerekiyor. En düşük uçuş maliyetini sağlayacak biçimde bu şehirleri hangi sırayla ziyaret etmelisiniz? Ya da bir kargoyu mümkün olan en hızlı ve verimli şekilde varış yerine ulaştırmak nasıl mümkün olur?
Bu ve bu gibi problemler gezgin satıcı problemi kapsamında incelenir. Çözüm için çok sayıda olası kombinasyon arasından her makul yolu incelemek, o yol için gereken mesafeyi (veya zamanı) ölçmek ve sonra en kısa (veya en hızlı) olanı seçmek gereklidir.
Ancak asıl sorun bunun nasıl yapılacağıdır. En kısa çözümü bulduğunuzdan emin olmak için onu olası tüm çözümler ile karşılaştırmanız gerekecektir. Cevabınız ise bilgisayarınızın gücü ve algoritmanızın yapısı ile ilişkili olacaktır. Bu nedenle de gezgin satıcı problemi, teorik bilgisayar bilimcilerinin verimli hesaplamanın sınırlarını test etmek için tekrar tekrar başvurdukları bir avuç temel problemden biridir
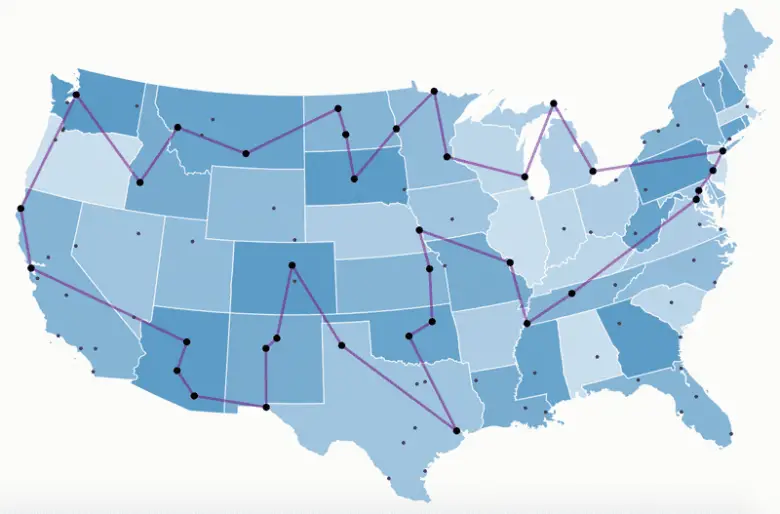
Gezgin Satıcı Problemi İle İlgili Sorun Nedir?
Bir algoritmanın görevini tamamlaması için gereken süre, yürütmesi gereken adım sayısıyla orantılıdır. Belki n tane yer için problemi çözmek için n2 adım atan bir algoritma bulabilirsiniz. Bu, on yeri ziyaret etmek istiyorsanız 100 adım ve 20 yer için 400 adım anlamına gelir.
Bu rakamlar size kötü gibi gözüktü ise hazır olun. Bir başka algoritmanın sorunu çözmek için 2n adım attığını hayal edin. O zaman on yer için 1.024 adım gerekecektir. Sayı büyüdükçe de ortaya çıkan adım sayısı korkutucudur.
Bu nedenle n2, n3 veya n4 gibi n’nin kuvvetlerini içeren ifadelere n’ye bağlı polinomlar denir. Bir algoritma n sayısının büyümesi ile orantılı bir biçimde büyür ise bu makul bir büyüme kabul edilecektir. Peki gezgin satıcı problemini çözmek için bir polinom zamanlı algoritma var mı? Cevabı henüz kimse bilmiyor.
P, elektronik tablodaki bir sayı sütununu sıralamak veya haritada iki adres arasındaki en kısa yolu bulmak gibi verimli bir şekilde çözebilecekleri problem sınıfını temsil eder. Yani bilgisayarlar bu tür problemleri kolayca halleder. Bu algoritmalar da verimli algoritmalardır. Verilen iki sayının en küçük ortak katını bulma, bir sayının asal olup olmadığını saptama, dört işlem aritmetik hesapları P sınıfındaki problemlerdir.
NP, bilgisayarların çözümleri verimli bir şekilde doğrulayabildiği problem sınıfını temsil eder. NP’nin aslında bir alt küme olarak P içerdiğine dikkat edin, çünkü bir sorunu doğrudan çözmek, çözümü doğrulamanın bir yoludur. P ve NP arasındaki ilişkiyi yukarıdaki Venn şeması ile de kolayca görebiliriz.
P sınıfındaki problemleri çözmek nispeten kolaydır. Sonucunda bir bilgisayar algoritması bunları uygun bir sürede çözecektir. Ancak NP sınıfındaki problemler için aynı şeyi söylemek olası olmayacaktır. Gezgin satıcı problemi de NP sınıfındaki problemlerden biridir.
Gezgin Satıcı Problemi Çözülürse Ne Olur?
Hücre biyolojisinden oyun teorisine kadar, P’ye karşı NP sorusu bir çok bilim dalı ve endüstriyi ilgilendiriyor. Eğer P = NP ise (yani Venn diyagramımız tek bir daireye dönüşür ve bu zor görünen problemler için hızlı algoritmalar elde edebilirsek) o zaman tüm dijital ekonomi çökmeye karşı savunmasız hale gelir.
Bunun nedeni, kredi kartı numaranız ve şifreleriniz gibi şeyleri güvence altına alan kriptografinin yalnızca gizli anahtarı bildiğiniz takdirde çözülmesi kolay olabilecek, hesaplama açısından zor problemleri temel alarak çalışmasıdır.
İşte bu nedenle, gezgin satıcı problemini çözmek için verimli bir algoritma bulduğunuz zaman, dünyanın en gizli kodlarının anahtarı olan milyon dolarınızı alacaksınız ve muhtemelen hayatınız artık güvende olmayacaktır. Biri bunun hakkında bir film yapmalı diye düşünebilirsiniz. Aslında yapıldı.
Beyazperdede Gezgin Satıcı Problemi
Gezgin Satıcı sorunu 2012 yılında beyaz perdeye de yansıdı. Traveling Salesman adlı bir film, ABD ordusuna P = NP problemine bir çözüm verip vermemeye karar vermesi gereken dört matematikçinin hikayesini anlatıyordu. Filmin fragmanına buradan göz atabilirsiniz.
Kaynaklar ve İleri Okumalar:
- One-Way Salesman Finds Fast Path Home. Yayınlanma tarihi: 5 Ekim 2017; Kaynakk: Quanta magazine. Bağlantı: One-Way Salesman Finds Fast Path Home/
- The Travelling Salesman Problem. Yayınlanma tarihi: 22 Ekim 2022; kaynak: Plus Math: Bağlantı: The Travelling Salesman Problem/
- This 90-year-old math problem shows why we need quantum computers. Yayınlanma tarihi: 4 haziran 2020. kaynak site: Big Think. Bağlantı:This 90-year-old math problem shows why we need quantum computers
Matematiksel
