İstatistikler, çevremizdeki dünyadaki kalıpları anlamak için yararlı bir araçtır. Ancak konu bu kalıpları yorumlamaya geldiğinde sezgilerimiz bizi çoğu zaman yarı yolda bırakır. Buna bir örnek Simpson Paradoksu olacaktır.

İstatistik verileri toplar, analiz eder ve yorumlar. Yorumlama esnasında da etiğin ön planda olduğu kabul edilir. Ancak verilerle, dikkatli olmamız gerekir. Nereden geldi? Nasıl elde edildi? Ve gerçekten ne diyor? Bunların hepsi, veriler sunulduğunda sormamız gereken iyi sorulardır.
Günümüzde araştırmacılar, verileri kolayca analiz edebilen ve karmaşık istatistiksel testlerin sonuçlarını çıkarabilen çok sayıda yazılım paketine erişebilmektedir. Ancak tam bir istatistiksel anlayışa sahip olmayan kişilerin bir veri kümesindeki bazı detayları yanlış anlamaları, son derece yanlış sonuçlara varmalarına yol açacaktır. Kimi durumlarda Simpson’s Paradoksunun da bize gösterdiği gibi, belirli bir veri kümesinden elde edilen bir sonuç, aynı veri kümesi alt gruplara bölündüğünde tersine çevrilecektir.
Simpson Paradoksu İle Nasıl Tanıştık?
Simpson’ın Paradoksu, istatistikçiler arasında farklı isimlerle bilinir. Edward H. Simpson İngiliz İstatistikçi, şifre kırıcı ve kendi adıyla anılan Simpson Paradoksunun yaratıcısıdır. Bu Paradoks, 1951 yılında yayınladığı “The Interpretation of Interaction in Contingency Tables – Acil Durum Tablolarında Etkileşim Yorumu” adlı makalede yer alır. Ancak bu garip durumu gören ilk kişi o değildir.

1903’te Udny Yule ve 1899’da Karl Pearson da benzer bir kavramdan bahsetmektedir. Bu nedenle paradoks Yule-Simpson etkisi olarak da adlandırılır. Simpson Paradoksu, bize verilerin tek başına tüm sorunların derdine deva olamayacağı gerçeğini gösterir. Ayrıca verilere dayalı olarak her zaman doğru tahminlerde bulunamadığımızı hatırlatır.
Simpson Paradoksunun ne zaman ortaya çıkacağını kestirmek güçtür. Spor, sağlık, eğitim, sosyal bilimler gibi pek çok alanda bu paradoksa rastlamak mümkündür. Bilinen bir örnek aşağıdaki gibidir.
Simpson Paradoksu İle İlgili Örnekler
Birkaç gün sonra kardeşinizin doğum günü ve kutlama için restoran seçme işini sizin yapmanız gerekiyor. İnternette yaptığınız bir araştırmadan sonra, incelemelerde 4,5’ten fazla puan alan A adlı bir restoranı seçtiniz. Ancak B restoranı da fena gözükmüyor. Durumu arkadaşlarınıza danıştığınızda onlar emin olmak için incelemeleri 40 yaş altı ve 40 yaş üstü olarak ikiye ayırmaya karar verdiler.
Bu analiz iki grubun aslında çevrimiçi derecelendirmesi 4,2 olan B restoranını tercih ettiğini gösteriyor. Peki ama grubu böldükten sonra ne değişti? Aslında değişen bir şey yok, sadece Simpson’s Paradoksuna sıkışıp kaldınız. Ne demek istediğimizi daha iyi anlamak için aşağıdaki tabloya göz atabilirsiniz.
| 40 Yaş Altı | 40 Yaş Üstü | ||
| A restoranını seçen kişilerin oranı | 80/100 = % 80 | 370/400 = % 92.5 | 450/500 = % 90 |
| B restoranını seçen kişilerin oranı | 326/400 = % 81.5 | 94/100 = % 94 | 420/500 = % 84 |
A ve B restoranına yapılan toplam yorumları karşılaştırıldığında,% 90’ının birinciyi tercih ettiği; ancak % 84’ünün ikincisini tercih ettiği görülmektedir. Fakat incelemeler iki gruba ayrıldığında, B restoranı daha çok tercih edilen olarak karşımıza çıkıyor.
Simpson paradoksu bize, bazen verilerin söylediği şey ile gerçeğin birbiri ile aynı olmadığını gösteriyor. Farklı gruplarda ortaya çıkan eğilimler, bu gruplara ait veriler birleştirildiğinde ortadan kaybolabilir. Bu gerçekleştiğinde ise genel eğilim, her gruptaki eğilimlerin tam tersi gibi görünecektir. Örneğin aşağıdaki örneği ele alalım.
Sayılar ile Uğraşırken İstatistiksel Yanılsama Mümkündür
1970’lerde, U.C. Berkeley okulunun yüksek lisans kabul programının başı Simpson Paradoksuyla dertteydi. Üniversiteye kabul esnasında cinsiyet ayrımı yaptığı gerekçesiyle dava edilmişti. Başvurularda toplanan istatistiksel verilere bakıldığında başvuru yapan erkeklerin % 44’ü kadınların ise % 35’i üniversiteye kabul edilmişti.
Rakamlar incelendiğinde cinsiyet ayrımı suçlamasının doğru olduğu sonucuna varılacaktır. Oysaki durum bundan farklıdır. Veriler gruplandırılmamış yani ham verilerdir. Mahkeme tarafından veriler bölüm bölüm gruplandırılınca ortaya şöyle bir tablo çıkar:
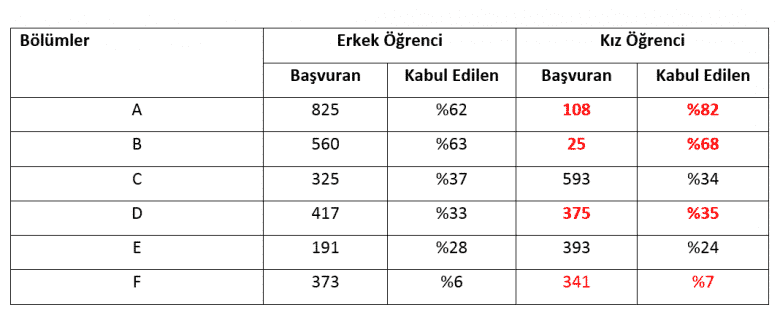
Tabloya bakıldığında kadın öğrenciler, üniversitenin en büyük 6 bölümünün 4’ünde erkek öğrencilere göre daha fazla kabul almıştır. Yani A, B, D ve F bölümlerine kabul gören erkek sayısı kadın sayısına göre daha azdır. Şöyle ki erkekler en fazla öğrenci kabul edilen bölüme başvuruyu daha fazla yaparken kız öğrenciler ise en az öğrenci kabul edilen bölüme daha fazla başvuru yapmıştır. Bu sebeple grup yüzdeleri ile toplam yüzdeleri birbirinden farklılık göstermektedir. Konuyu pekiştirmek için başka bir örnekle devam edelim.
Paradoks ile İlgili İkinci Bir Örnek
Bu paradoksun bir örneği, bir tedavinin tüm hasta gruplarında zararlı olabileceği, ancak gruplar birleştirildiğinde genel olarak faydalı görünebilmesidir. Önerilen bir tıbbi tedaviye ilişkin bir denemeyi ele alalım.
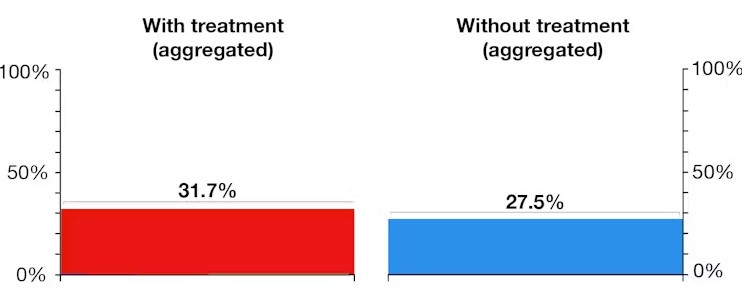
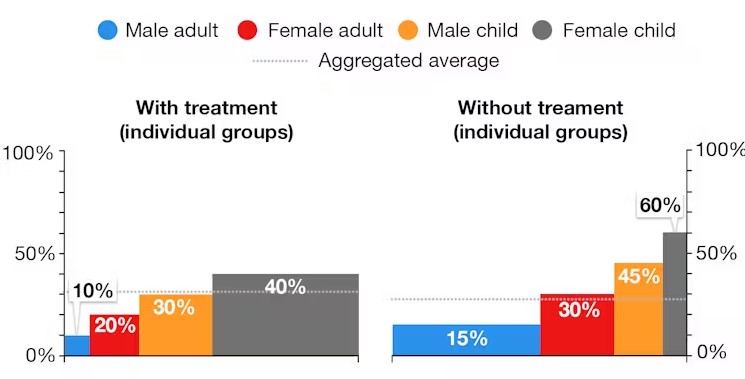
120 hastadan oluşan bir grup (10, 20, 30 ve 60’lık alt gruplara bölünmüş) tedavi almakta ve aynı koşullarda 120 hasta da tedavi almamaktadır. Genel sonuçlar, tedavinin hastalar için faydalı olduğunu gösteriyor. Yani tedavi gören hastalarda iyileşme oranı, tedavi görmeyenlere göre daha yüksek durumda.
Bununla birlikte, çalışmadaki grupları derinlemesine incelediğinizde, tüm hasta gruplarında, tedavi görmeyen hastalarda iyileşme oranının daha yüksek olduğunu görürsünüz. Ancak her grubun büyüklüğü ve yaş dağılımının farklı olduğunu unutmayın. Rakamları çarpıtan şey de aslında budur. Bu örneğimizde tedavi uygulanan grup orantısız bir şekilde çocuklardan oluşuyordu. Doğal olarak da tedavi olsun ya da olmasın iyileşme oranlarının daha yüksek olması normaldi.
Sonuç Olarak
Gördüğünüz gibi, hasta sayısının dikkatsizce seçildiği bir deneme, zararlı bir tedavinin faydalı göründüğü sonucuna varılmasına neden olacaktır. Bu nedenle araştırmacıların çalışmalarına başlamadan önce Simpson paradoksunun farkında olmaları gereklidir. Simpson paradoksu istatistiğin çarpıtılabileceğini, farklı bakış açıları ile farklı sonuçların elde edilebileceğini gözler önüne serer. Yazının devamında göz atmak isterseniz: Tip 1 ve Tip 2 Hata Nedir? Neden Dikkat Etmemiz Gerekir?
Kaynaklar ve ileri okumalar:
- Altman, Douglas G and Jonathan J Deeks, 2002. “Meta-Analysis, Simpson’s Paradox, and the Number Needed to Treat”. BMC Medical Research Methodology, 2: art. 3. doi:10.1186/1471-2288-2-3
- Armistead, Timothy W., 2014, “Resurrecting the Third Variable. A Critique of Pearl’s Causal Analysis of Simpson’s Paradox”, The American Statistician, 68(1): 1–7. doi:10.1080/00031305.2013.807750
- Carlson, Bruce W.. “Simpson’s paradox”. Encyclopedia Britannica, 2 Apr. 2024, https://www.britannica.com/topic/Simpsons-paradox. Accessed 19 May 2024.
- Bandyopadhyay, Prasanta S., Davin Nelson, Mark Greenwood, Gordon Brittan, and Jesse Berwald, 2011, “The Logic of Simpson’s Paradox”, Synthese, 181(2): 185–208. doi:10.1007/s11229-010-9797-0
- Maths in a minute: Simpson’s paradox; Kaynak site: Plus Math. Yayınlanma tarihi: % Kasım 2010. Bağlantı: https://plus.maths.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel