Dünya yüzeyinden bir çok uygarlık geldi ve gitti. Bunun birçok nedeni olsa da çoğu çöküşün birincil nedeni kaynakların aşırı tüketimi ve toplumdaki eşitsizlikler idi. Peki, günümüz toplumunun çöküşü yakın mı? Lotka Volterra Denklemi olarak bilinen bir çift denklem bu konuda bize bir cevap verebilir.

Aslında araştırmacılar bir süreden beri bu soruya cevap bulmayı umuyorlar. Human and nature dynamics (HANDY) adı verilen bir araştırmada toplumsal evrimin matematiksel bir çalışması yer aldı. HANDY, 1920’lerde iki matematikçi, Amerikalı Alfred Lotka ve İtalyan Vito Volterra tarafından bağımsız olarak türetilen klasik bir modelden esinlenmişti.
Lotka – Volterra Denklemi Nedir?
Hayatta kalmak kolay değil. Bu sözü bir metafor olarak kullanmadık. Vahşi doğada hayatta kalmak gerçekten önemli bir sorundur. Türler bu soruna evrimsel süreçlerde çözümler geliştirmişler ve bunun farklı yollarını bulmuşlardır. Hayatta kalma döngüsü bir avcı türün ve avının birbirleri ile ilişkisine bağlıdır.
1920’lerde Amerikalı matematikçi Alfred J. Lotka ve İtalyan matematikçi ve fizikçi Vito Volterra tarafından formüle edilen iki denklem Lotka-Volterra denklemleri olarak bilinir. Avcı-av denklemleri olarak bilinen bu denklemler, matematiğin biyolojiye uygulanmasının ilk örneklerinden biri olarak kabul edilir.
Bilim insanlarının çevreyi ve orada yaşayan hayvanları nasıl koruyacaklarını anlayabilmeleri için bilgi toplamaları gerekir. Bu esnada da ellerindeki en önemli araç aslında matematiktir. Matematiksel modelleme sayesinde yırtıcı hayvanlar ve av arasındaki ilişkiyi ortaya çıkarmak mümkün olur. Bu sayede bilim insanları popülasyonlarının zaman içinde nasıl değiştiğini anlayabilir. Bu da bir hayvanın ne zaman yok olma riskiyle karşı karşıya olabileceğini bilmelerini sağlayacaktır.

Lotka, 1910’da, otokatalitik kimyasal reaksiyonların yani kendilerini düzenleyen kimyasal süreçlerin oranlarını anlamanın bir yolu olarak bu denklemleri önerdi. 1926’da Vito Volterra’da İtalyan deniz biyoloğu Umberto D’Ancona ile tanıştıktan sonra konuyla ilgilenmeye başladı.
D’Ancona, Volterra’ya Adriyatik Denizi’nde ağlara yakalanan yırtıcı balıkların yüzdesinin I.Dünya Savaşı sırasında büyük ölçüde arttığını anlatmıştı. Bu değişiklik, savaş yıllarında balıkçılığın azalmasıyla bağlantılıydı, ancak bir gariplik vardı. Daha az balık avı sonucunda ağlarda her türden daha fazla balık olmalıydı ama bu çeşitlilik yoktu. Sonunda Lotka ile aynı denklemleri kullanan Volterra, hem avcı hem de av türlerindeki dalgalanmaları açıkladı.
Lotka – Volterra / Avcı Av Denklemleri Nasıl Çalışır
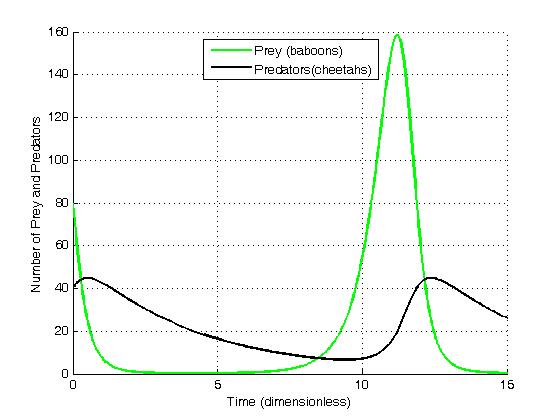
Lotka-Volterra denklemleri, biri yırtıcı, diğeri av olmak üzere iki türün etkileştiği biyolojik sistemlerin dinamiklerini tanımlamak için kullanılan bir çift birinci dereceden doğrusal olmayan diferansiyel denklemdir. Diferansiyel Denklemler, popülasyonların zaman içinde nasıl değiştiğini veya bir helikopterin nasıl uçtuğunu, gezegenlerin bir yıldızın yörüngesinde nasıl döndüğünü veya damarlarımızda kanın nasıl aktığını içeren diğer birçok süreci tanımlayan denklemlerdir.
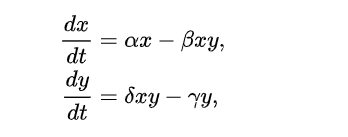
Lotka-Volterra denklem sistemi, ekolojik sistemlerin dinamiklerini avcı-av etkileşimleri, rekabet, hastalık ve karşılıklılık ile modelleyebilen daha genel bir çerçeve olan Kolmogorov modeline bir örnektir. Denklem av ve avcı popülasyonlarının birbirine bağlı olduğunu ortaya koyuyor.

Bu denklemlere göre, belli bir süre boyunca av ve avcı popülasyonları artar. Ancak, belli bir seviyeden sonra avcı popülasyonundaki aşırı artış avlanan nüfusunda azalmaya neden olur. Azalan besin kaynakları nedeni ile denklem zamanla tersine dönmeye başlar. Dışl bir faktör dengeyi bozana kadar denge bu şekilde devam eder.
Denklemler İle İlgili Bir Örnek: Vaşak – Tavşan İlişkisinin Modellenmesi
Bir matematikçi bir denklem geliştirirken dünyayı düşünür. Şimdi zaman içinde tavşan popülasyonuna neler olduğunu düşünelim. Aşağıdaki görselde ilk kısımda gördüğünüz vaşak olmasaydı gelecekteki tavşan popülasyonunu tahmin etmek için kullanılan denklemlerdir. Sonuç üstel büyüme biçimindedir.

İkinci kısım ise ( B) tavşan olmaması durumunda gelecekteki vaşak popülasyonunu tahmin etmek için kullanılır. Bu denklemler sonucun üstel düşüş olduğunu söyler. Üçüncü kısım ise popülasyonların etkileşim halinde olduğu bölümdür. ( C) Bu, hem tavşanlar hem de vaşaklar için dalgalanan popülasyon seviyeleri ile sonuçlanır.

Tür etkileşimlerinin sonucunu tahmin etmek, toplulukların nasıl yapılandığını anlamaya çalışan biyologların ilgisini çeker. Avcılar ve av, birbirlerinin evrimini etkiler. Bir avcının av bulma ve yakalama yeteneğini artıran özellikler avcıda evrimleşir. Avın yenilmekten kaçınma yeteneğini artıran özellikler de avda doğal seçilim yoluyla öne çıkacaktır. Bu denklemler bu sürecin işleyişini kavramamıza yardımcı olur.
Denklemler Geleceğimiz Hakkında Bize Ne Diyor?
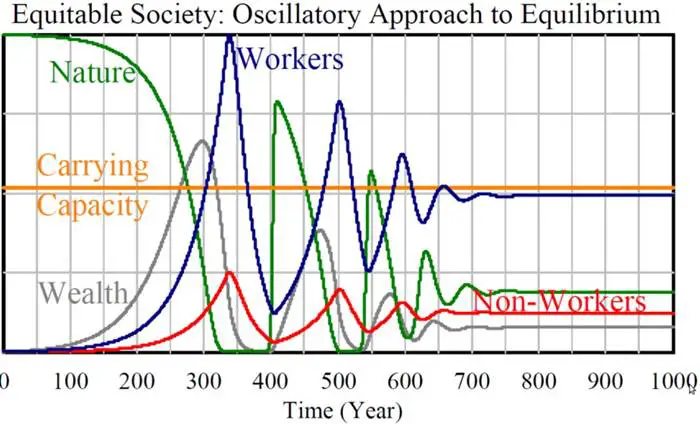
Lotka-Volterra denklemlerinin bazı sınırlamaları vardır. Ancak yazının başında da bahsettiğimiz HANDY, geri dönüşü olmayan bir çöküşü simüle etmek için kullanılabilir. Model, nüfusu her biri için ayrı bir denklemle zengin ve fakir olarak böler. Aynı zamanda doğal kaynakları ve birikmiş serveti de tahmin ederek dört bağlantılı denklem oluşturur. HANDY, doğal kaynaklara “av” iken, insanlara ise “yırtıcı” muamelesi yapar.
Adil bir toplumda HANDY, doğal kaynakların tüketimini azaltarak çöküşün önlenebileceğini göstermektedir. Ancak eşitlikçi olmayan toplumlarda ise çöküşten kaçınmak olanaksızdır. Çökmeye yol açan iki ana faktör, kaynakların azalması ve toplumun ekonomik açıdan tabakalaşmasıdır.
Bunun önlenmesi için tek çare doğanın kaynaklarının verimli kullanılması ve eşit bir biçimde dağılmasıdır. Matematik ne yazık ki geleceğimizin çok da parlak olmadığını bize hatırlatıyor. Ayrıca merak ederseniz: Normal Bitkiler Nasıl Etçil Bitki Haline Geldi?
Kaynaklar ve ileri okumalar için:
- Lotka–Volterra equations; https://en.wikipedia.org/
- Brady R and Butler J (2021) The Circle of Life: The Mathematics of Predator-Prey Relationships. Front. Young Minds. 9:651131. doi: 10.3389/frym.2021.651131; Bağlantı: https://kids.frontiersin.org/
- The Future of Society: Prosperity or Collapse?Yayınlanma tarihi: 15 mayıs 2014; Bağlantı: https://thatsmaths.com/2014/05/15/the-future-of-society-prosperity-or-collapse/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel