İnsanlık tarihinin en önemli buluşlarından biri tekerlektir. Peki ama bir tekerlek neden çember biçimindedir? Cevap geometride yatar. Çember sabit bir çapa sahiptir bu da cismin düzgün bir biçimde hareket etmesini sağlar. Ancak, sabit çapa sahip şekil sadece çember değildir. Aynı şeyi bir Reuleaux üçgeni ile de başarabilirsiniz.

Eğer canınız sıkılır, elinize bir pergel ve cetvel alıp çeşitli şekiller çizerseniz muhtemel kenarları yay biçiminde her türlü ilginç şekli keşfedebilirsiniz. İşte bu şekillerden birisi de Reuleaux üçgeni olacaktır. Alman bilim insanı ve mühendis Franz Reuleaux (1829–1905) modern kinematik ve makine tasarımının kurucusu olarak kabul edilir. Reuleaux’nun adı, Reuleaux üçgeni ile ölümsüzleşmiştir.
Reuleaux Üçgeni Nedir? Nasıl Çizilir?
Reuleaux üçgeni, bir eşkenar üçgenin her bir köşesinde eşit yarıçaplara ve merkezlere sahip üç dairesel yaydan oluşur. Bu şekli siz de kolayca yapabilirsiniz. Bunun için önce bir kenarı x cm uzunluğunda olan bir eşkenar üçgen çizin.
Şimdi bir pergel alan ve genişliğini x cm olarak ayarlayın. Pergelin ucunu köşelerden birine koyun ve karşısında kalan iki köşeden geçecek biçimde bir çember çizin. Bu işlemi üç defa tekrarlayın. Aşağıdaki görselde mavi boyalı kısım bir Reuleaux üçgenidir. Bu şeklin de aynı çember gibi sabit bir genişliği vardır. Sonucunda bu da onu birçok amaç kullanılan yararlı bir geometrik şekil yapar.
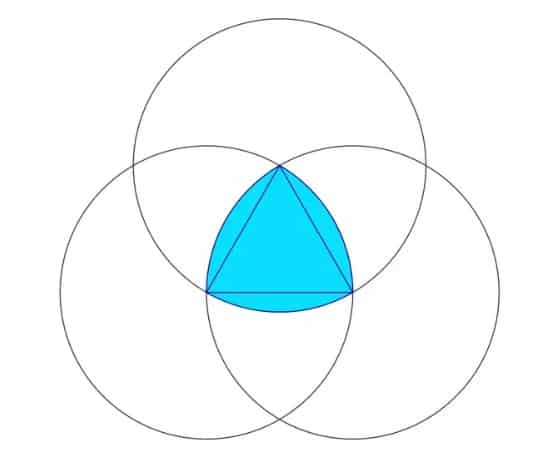
Örneğin bu şekle uygun biçimde inşa edilen bir aracı, bir şeyleri dengeli bir biçimde yuvarlamanız gerektiğinde kullanabilirsiniz. Ancak hatırlatalım. Tam olarak bir tekerlek görevini elbette görmeyecektir. Çünkü tekerlekler aksa ihtiyaç duymaktadır. Ancak Reuleaux üçgeni biçiminde tasarlayacağını bir tekerlek üzerinde, aks yukarı ve aşağı hareket edecek ve bu da onu kullanışsız hale getirecektir.
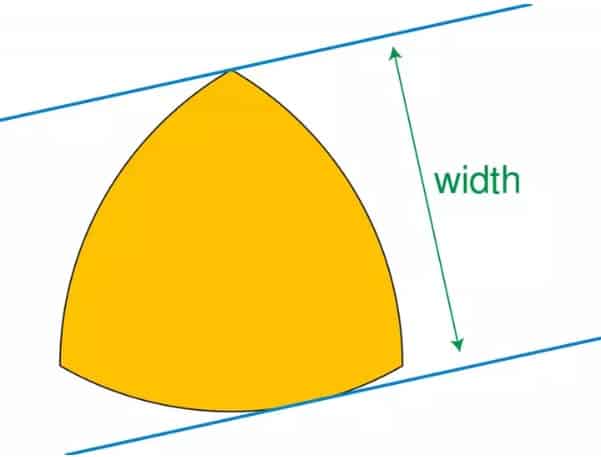
Reuleaux üçgeninin genişliği sabittir. Bu nedenle de bir tanesi köşelerden geçmek şartıyla üçgene iki paralel doğru çizildiğinde, bu iki doğru arasındaki mesafe her zaman birbirine eşit olacaktır. Onun bu özelliği bize çemberi hatırlatır. Aslında iki şeklin de birçok ortak özelliği vardır. Örneğin Reuleaux üçgeninin çevresi ile bir çemberin çevresi birbirine eşittir.
Reuleaux üçgeninin bir başka şaşırtıcı özelliği de, Reuleaux üçgeni şeklindeki bir matkap ucunun beklenen yuvarlak delik yerine kare şeklinde bir delik açabilmesidir. Ya da başka bir deyişle, bu üçgen her zaman uygun büyüklükte bir karenin her iki kenarıyla temas halindedir.

İngiliz mühendis Harry James Watt, 1914’te bu matkapların üretilmesi için gerekli patenti aldı ve kare biçiminde delik yapabilen matkapların üretimine, 1916’da başlandı.
Günlük Hayatımızda Reuleaux Üçgeni
Alman bir mühendis olan Felix Wankel (1902–1988) tarafından tasarlanan Wankel motoru Reuleaux üçgeni biçiminde döner bir parçaya sahip içten yanmalı bir motordur. Bu motorun daha az hareketli parçası vardır ve boyutuna göre normal pistonlu motorlardan daha fazla güç üretir. Wankel motoru ilk olarak 1957’de denendi ve ardından 1964 Mazda’da üretime alındı.
Ancak bir Reuleaux üçgeni görmek istiyorsanız aslında çoğu durumda elinizdeki kurşun kalemlere de göz atmanız yeterli olacaktır. Aşağıdaki görselde de gördüğünüz gibi, bu tasarım kalemin daha iyi bir şekilde kontrol edilmesini sağlayan bir parmağı desteklemektedir.

Modern mimaride de bu üçgen bir çok yerde karşımıza çıkar. Örneğin Almanya, Köln’de Kölntriangle olarak adlandırılan bir binayı aşağıda görebilirsiniz. Üçgenin kıvrımları, binanın üç yanından panoramik manzaraya sahip olmasını sağlar.

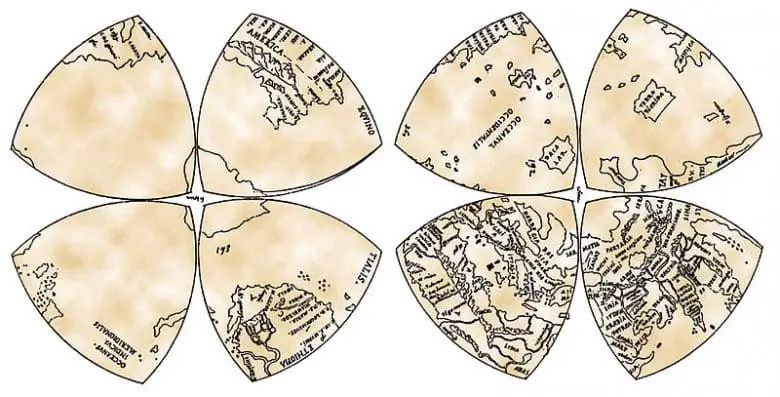
Biz bu üçgeni modern zamanlarda tanımlasak da Leonardo da Vinci, Reuleaux Üçgeni’nin geometrisine dayalı olarak dünya haritaları yapmıştır. Her bir üçgen dünyanın 1/ 8’ini temsil eder. Bu harita Leonardo da Vinci’nin Mappa mundi’si olarak adlandırılmaktadır.
Reuleaux üçgeninin sıra dışı özelliklerinin hayatımızda karşımıza çıktığı daha bir çok yer vardır. Üç eşit eğimli kenarı ve sabit eğri genişliği, onu birçok uygulama için cazip kılar. Yapısal kararlılığı ve küçük çevresi, mimari ve mekanik tasarımlarda onu tercih sebebi yapar.

Bu yazıdan sonra etrafınıza daha dikkatli bakarsanız muhtemel siz de bu üçgenlerden bir kaçına rastlarsınız. Biraz daha örnek mi? Mesela çoğu yerde karşınıza çıkan bir rögar kapağını Reuleaux Üçgeni tasarımıyla görmeniz olası olabilir. Şimdi bu yazıya göz atabilirsiniz: Rögar Kapakları Neden Hep Yuvarlak Olur?
Kaynaklar ve ileri okumalar:
- Alfred S. Posamentier and Robert Geretschläger; The Circle: A Mathematical Exploration beyond the Line; Prometheus Books, 2016
- New £1 coin gets even; yayınlanma tarihi: 13 Aralık 2016; Bağlantı: https://plus.maths.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










