Başlıkta okuduğunuz soru size saçma gelse de yapacağınız küçük bir aramada sorunun popülaritesi sizi şaşırtacaktır. Bunun nedeni geçtiğimiz yıllarda işe alım mülakatları esnasında başta Microsoft olmak üzere bazı teknoloji devlerinin bu soruyu sorması ve devamında da elbette cevabının merak edilmesidir.

Baştan söyleyelim, “deliğin içine düşmemesi için” biçiminde vereceğiniz bir cevap işe kabul edilmeniz için yeterli değildir. Aslında “Rögar kapakları neden yuvarlak olur?” sorusunun birden çok cevabı olasıdır. Basit cevap kapaklar yuvarlaktır çünkü rögarlar yuvarlaktır biçiminde de olabilir. Ancak gerçek cevap bundan biraz daha detaylıdır.
Hepimizin bildiği ve yollarda bol olarak gördüğü tesisat deliği veya kanalizasyon deliği olarak da bilinen rögarlar; denetimler, onarımlar ve bağlantılar yapmak gibi çeşitli amaçlar için kullanılan bir yeraltı bacasıdır. Bu açıklığı kapama işini de elbette rögar kapağı yapar. Kapaklar tipik olarak dökme demir, beton veya ikisinin bir kombinasyonundan yapılır. Bu da onları dayanıklı, ucuz ve oldukça da ağır yapar. ( Bir kapak yaklaşık 50 kilogram kadar).
Rögar Kapakları Neden Kare Değil de Yuvarlaktır?

Kapaklarının yuvarlak olmasının akla ilk gelen en basit nedeni kapağın etrafındaki toprak basıncına dayanıklılığı artırmaktır. Yuvarlak şekil, basınca karşı en uygun şekildir. Ayrıca yuvarlak kapak üretmek kare ya da dikdörtgen kapak üretmekten çok daha kolaydır. Son olarak yuvarlık bir kapağın bir yerden başka bir yere yuvarlanarak taşınması daha kolaydır.
Şimdi burada duralım. Yukarıda saydığımız özelliklerin bir çoğu aslında bir Reuleaux üçgeni içinde geçerlidir. Yani aslında rögar kapaklarını kesinlikle Reuleaux üçgeni biçiminde de yapmak mümkündür. Aşağıda Reuleaux üçgeni biçiminde bir rögar kapağı görebilirsiniz.

Reuleaux Üçgeni biçiminde bir rögar kapağı asla aşağıya düşemez. Ayrıca bu tip kapakların kullanılması malzemeden de tasarruf sağlayacaktır.
On dokuzuncu yüzyıl Alman mühendisi Franz Reuleaux (1829-1905), makineleri ve yapılarını anlamamız üzerinde önemli bir öncü etkiye sahipti. Sabit genişliğe sahip olan ve düzgün bir şekilde yuvarlanan ancak daire olmayan bir şekil arayışındayken de bu üçgeni bizlere kazandırdı. Ancak yine de yaygın kullanılmamalarının arka planında da geçerli bir neden vardır. Bu da üretimlerinin kolay olmamasıdır.
Reuleaux Üçgeni Nedir?
Reuleaux üçgeni, kenarları kıvrımlı bir üçgendir. Bu üçgen bir çok açıdan bir daire ile benzeşir. Örneğin bir daire gibi bu üçgen de sabit bir genişliğe sahiptir. Reuleaux üçgeni, bir eşkenar üçgenin her bir köşesinde eşit yarıçaplara ve merkezlere sahip üç dairesel yaydan oluşur.
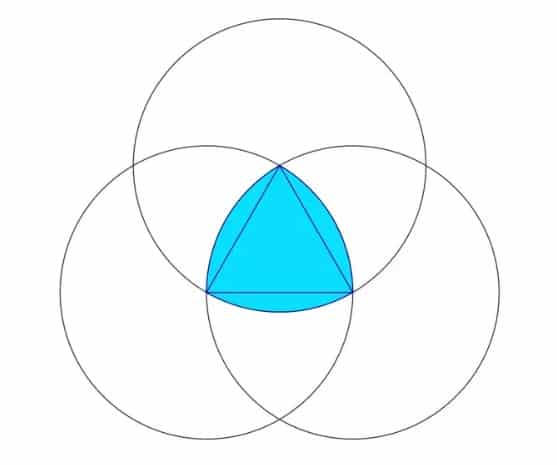
Reuleaux Üçgeni Şaşırtıcı Özellikleri Olan Bir Şekildir
Reuleaux üçgeninin genişliği sabittir; bir tanesi köşelerden geçmek şartıyla üçgene iki paralel doğru çizildiğinde, bu iki doğru arasındaki mesafe her zaman birbirine eşit olacaktır. Onun bu özelliği bize çemberi hatırlatır ve aslında iki şeklin birçok ortak özelliği vardır. Reuleaux üçgeninin çevresi, bir çemberin çevresi ile eşittir. Sabit genişliği nedeniyle bir Reuleaux üçgeni pek konforlu bir sürüş deneyimi vermese de en azından teoride tekerlek olarak da kullanılabilir.
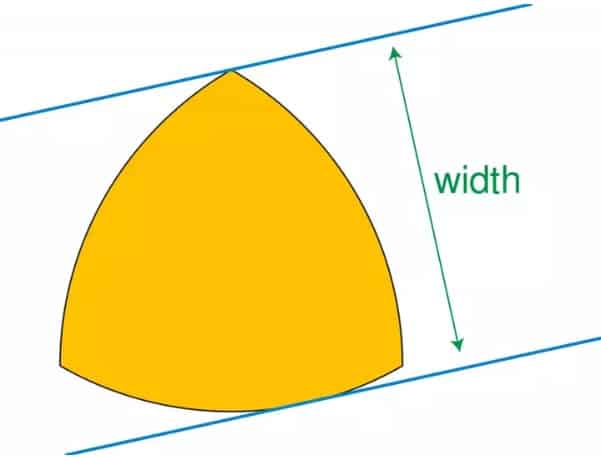
Ancak iki şeklin alanlarının karşılaştırılması, Reuleaux üçgeninin alanının dairenin alanından küçük olduğunu gösterir. Bu, dairenin belirli bir çap için en büyük alana sahip olduğu normal çokgen anlayışımızla tutarlıdır. Reuleaux üçgeninin bir başka şaşırtıcı özelliği de, Reuleaux üçgeni şeklindeki bir matkap ucunun, beklenen yuvarlak delik yerine kare bir delik açabilmesidir. Ya da başka bir deyişle, Reuleaux üçgeni her zaman uygun büyüklükteki bir karenin her iki kenarıyla temas halindedir.
Gördüğünüz gibi eğer bir gün bir yerde “Rögar kapakları neden yuvarlak olur?” sorusu ile karşılaşırsanız verebileceğiniz bir çok cevap vardır. Üstüne üstlük bir de alternatif şekil olarak Reuleaux üçgeninden bahsederseniz işi kapmanız bile olası olabilir.
Kaynaklar ve ileri okumalar:
- Manhole cover; https://en.wikipedia.org/
- JOHN D. BARROW; 100 Essential Things You Didn’t Know You Didn’t Know about Math and the Arts, Yayıncı: W. W. Norton & Company; Reprint edition; ISBN-10 : 0393352226
- Why Are Manhole Covers Round?; yayınlanma tarihi: 222 Temmuz 2022. Kaynak site: Live Science. Bağlantı: Why Are Manhole Covers Round?;
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





