Everest Dağının Yüksekliği Matematik Yardımı İle Nasıl Ölçüldü?

Dünyanın en yüksek zirvesinin yüksekliğini kim hesapladı ve Everest Dağı’nı kim keşfetti? Bu sorunun cevabı George Everest değildir. Bir dağın yüksekliğini ölçmek, günümüz mevcut teknolojisinin olmadığı bir zamanda, matematik sayesinde mümkün olmuştur.

Keşiflerin altın çağında kaşiflerin ziyaret ettikleri bazı yerlere kendi isimlerini vermeleri sık karşılaşılan bir durumdur. Ancak aynı durum George Everest için geçerli değildi. Aslında George Everest, kendi adını taşıyan dağı hiçbir zaman kendi gözleriyle göremedi.

Everest Dağının Yüksekliği Nasıl Ölçüldü?

Everest dağının yüksekliğinin ilk ölçümü ise Hindistan alt kıtasını bilimsel hassasiyetle incelemeyi amaçlayan uzun soluklu bir proje olan Hindistan’ın Büyük Trigonometrik Araştırma (Great Trigonometrical Survey) kapsamında gerçekleşti.

Londra’nın Greenwich ilçesinde köklü bir ailenin çocuğu olarak dünyaya gelen Everest, askeri kariyerini Hindistan’da sürdürmek için 16 yaşında memleketinden uzaklaşacaktı. Matematik ve astronomi konusundaki yeteneği sonucunda da kısa süre içinde kendisini çeşitli ölçüm görevlerinde bulacaktı. Sonunda da 1818’de Büyük Trigonometrik Araştırma Projesinde çalışmaya başladı.

Bu proje, o dönemde Hindistan’daki coğrafi bilgi eksikliklerini gidermeyi ve daha doğru haritalar oluşturmayı hedefleyen büyük çaplı bir coğrafi ölçüm ve haritalama girişimiydi. Everest’e bu esnada sıkıcı bir görev verilmişti. Kendisinin görevi yarımadanın güney ucundan Nepal’e kadar yaklaşık 2.400 kilometre boyunca bir meridyen yayını ölçmekti.

Görev sıkıcı olsa da Everest işine bağlı biriydi. Görevinde terfi edecek ve çalışmalarını 1843 yılında emekli olana kadar devam ettirecekti. Emekli olup İngiltere’ye döndükten sonra Hindistan’daki görevi, öğrencisi Andrew Scott Waugh’e verildi.

Radhanath Sikhdar Everest Dağının Yüksekliğini Ölçen İlk Kişiydi

Bu sıralarda da Hintli bir matematikçi olan Radhanath Sikhdar, Peak XV adını verdiği bir dağın yüksekliğini hesaplamıştı. Hesaplamaları bu dağın yüksekliğinin 8.839,2 metre olduğunu gösteriyordu. Sikdar, Himalaya dağ silsilesinin haritasını çıkarmaya yönelik istihbarat projesinde, baş araştırma görevlisiydi. Sahip olduğu takım liderliği pozisyonuna nedeniyle de o zamanlar ‘Baş Bilgisayar’ olarak isimlendiriliyordu. Hesaplamaların doğrulanması birkaç yıl aldı ve 1856’da sonuçları duyuruldu.

Dünyadaki zirvelerin en yükseği için önerilen isim ise Everest Dağı olacaktı. Uzun bir tartışmanın ardından, Waugh’un önerdiği isim nihayet 1865’te resmi olarak kabul edilecekti.  

Yükseklikleri Ölçmek İçin Trigonometri Her Zaman İşe Yarar

Trigonometri, günümüzden çok önce Yunanlılar tarafından yüksek yapıları ölçmek için ve Victoria dönemi araştırmacıları tarafından da bir dağın yüksekliğini ölçmek için kullanılıyordu. Aslına bakarsanız günümüzde uydular da daha modern bir yaklaşım ile ancak esasen aynı prensibi uygulayarak dağın yüksekliği ölçmektedir.

Herhangi bir üçgende üç kenar ve üç açı vardır. Bu niceliklerden biri kenar olmak koşuluyla, üç değeri biliyorsak diğerlerini de hesaplayabiliriz. Dik açılı bir üçgende, açılardan biri zaten bilinmektedir. Bu durumda da herhangi bir açıyı ve kenarlardan birini biliyorsak, diğerleri de bulabiliriz. Bu ilke ile aslında sadece bir dağın değil, herhangi bir nesnenin yüksekliğini ölçmek her zaman mümkündür.

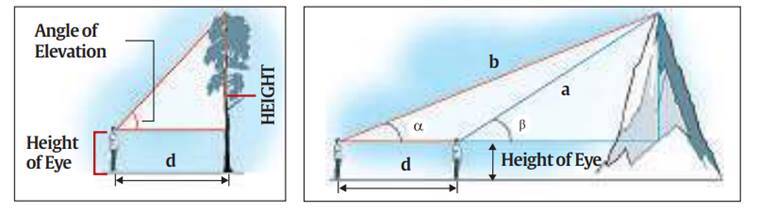
Diyelim ki bir direğin veya bir binanın yüksekliğini ölçmeniz gerekiyor. Öncelikle binadan biraz uzakta herhangi bir noktayı zeminde işaretleyerek işe başlamalıyız. Bu sizin gözlem noktanız olacaktır. Şimdi iki şeye ihtiyacınız var.

Bunlardan ilki binanın gözlem noktasına olan uzaklığıdır. Diğeri ise binanın tepesinin zemindeki gözlem noktası ile yaptığı açıdır. Mesafeyi hesaplamak bir çok durumda zor olmayacaktır. Yükselti açısını ölçmek için de aşağıda gördüğünüz gibi kullanmanız gereken bazı aletler bulunmaktadır. Bunun sonucunda gözlem noktasından binaya olan uzaklık d ise ve eğim açısı E ise, o zaman binanın yüksekliği d × tan(E) biçiminde olacaktır.

Ancak dağın zirvesini bilseniz bile tabanının nerede başladığı her zaman belirgin değildir. Bu nedenle de genel olarak bir dağın başlangıç noktası deniz seviyesi biçiminde kabul edilmektedir. Ayrıca dağa kadar olan mesafeyi hesaplamak da sorundur. Ancak bu sorunu da yine trigonometri yardımı ile çözeriz.

Bunu daha iyi anlamak için yukarıdaki görsele bir kere daha bakabilirsiniz. Bu durumda iki tane dik üçgen ile uğraşmanız gerekiyor. İki farklı gözlem noktası arasındaki mesafeyi de bildiğinize göre basit bir hesap ile dağın yüksekliğini bir kere daha yanına gitmeden ölçebilirsiniz.

Günümüzde Bir Dağın Yüksekliği Nasıl Ölçülüyor?

Yukarıda anlattığımız çözümler zirvesini görebildiğimiz tepeler ve dağlar için çoğu zaman doğruya yakın sonuçlar verecektir. Ancak söz konusu olan Everest gibi devasa yükseklikler ise işin içine başka şeyler de karışır.

Günümüzde dağların yüksekliğini ölçmek için genellikle GPS kullanılmaktadır. Ancak yüksek dağların ölçümleri esnasında yerçekimi de işini içine karışmaktadır. Bunun için tek başına GPS kullanımı da yeterli gelmez. Bu nedenle günümüzde, matematiğe dünyayı çevreleyen bir uydu ordusu da destek veriyor. konumunu hesaplar.

Şu anda deniz seviyesinden 8848 metre yükseklikte bulunan Everest Dağı, dünyanın en yüksek dağ zirvesidir. Ancak araştırmalar, tektonik faaliyetler nedeniyle Everest Dağı’nın yüksekliğinin sürekli arttığını göstermiştir. Bu nedenle yukarıda gördüğünüz gibi dağın yüksekliği için farklı sonuçlar elde edilmiştir.

Kaynaklar ve ileri okumalar

• Experts Explain: How to measure a mountain; Yayınlanma tarihi: 18 Aralık 2020; Bağlantı: https://indianexpress.com/
• Mount Everest: named after the first surveyor general of India. Yayınlanma tarihi: 21 Haziran 2011. Kaynak site: The Guardian. Bağlantı: Mount Everest: named after the first surveyor general of India/
• They Named Mount Everest After Him – But He Never Laid Eyes On It. Kaynak site: All Thats Interesting. Yayınlanma tarihi: 31 Mayıs 2018. Bağlantı: They Named Mount Everest After Him – But He Never Laid Eyes On It
• Shrinking Mount Everest: How to Measure a Mountain. Kaynak site: Livescience. Yayınlanma tarihi: 1 Mayı 2015; Bağlantı: Shrinking Mount Everest: How to Measure a Mountain

Size Bir Mesajımız Var!

Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel