Günümüzde sadece dekoratif amaçlı olarak kullansak da tarih boyunca bir çok kültür labirentlere farklı anlamlar yüklemiş ve hikayelerine dahil etmiştir. Bir labirent tasarlamak ve labirentten kurtulmak günümüzde bize kolay bir görev gibi gelse de bilgisayar bilimcileri ve matematikçiler labirent üreten algoritmalara hala oldukça düşkündür.

Labirent çizimleri ilk olarak kutsal yerlerde yaygın biçimde kullanılıyordu. Ancak sonrasında bir oyun olarak görülmeye başladı. Daha sonra da, genellikle görkemli evlerin arazisinde bulunan ünlü çit labirentlerine dönüştü. Bunun bir örneği İngiltere’deki en ünlü labirentlerinden biri olan ve tarihi, 17. yüzyılın sonlarına kadar uzanan Hampton Court labirentidir..

Labirentler antik anlatılarda da sıklıkla karşımıza çıkar. Bunlardan en önemlisi aşağıda görselini gördüğünüz Girit labirentidir. Ancak aslında bu labirentte karşımıza çıkan geometrik desen birçok farklı kültürde görülür. Desen, küçük bir alana çok uzun bir yol sığdırdığı için ayrıca matematikçilerin de ilgisini çeker.

Bir Labirent İnşa Edelim
Geleneksel bir Girit Labirenti çizmek için işe bir çekirdek ile başlamak gerekir. Görüntüsü kafa karıştırıcı olsa da aslında oluşturması oldukça kolaydır. Tek yapmanız gereken aslında eğriler aracılığıyla noktaları birleştirmektir. Ancak bu işlemi yaparken de yolu olabildiğince uzatmak adına çaba göstermeniz gerekir. Aşağıdaki çizimi dikkatle takip ederseniz bunu kolayca anlayabilirsiniz.

Yukarıda çizmiş olduğunuz labirent karmaşık görünmesine rağmen, bu labirentten kurtulmak oldukça kolaydır. Merkeze giden yol çok uzun olmasına rağmen, sadece bir giriş ve bir çıkış yolu vardır. Bu yüzden herhangi bir karar vermek zorunda kalmazsınız. Tek yapmanız gereken yürümektir. Bu arada hatırlatalım. Başlangıç şeklini değiştirerek farklı labirentler çizmeniz de mümkündür.
Bir Labirentten Kurtulmak İçin Kullanabileceğiniz Bir Kaç Metot Mevcuttur
Labirentler ‘basit bağlantılı’ ve ‘çoklu bağlantılı” olmak üzere ikiye ayrılır. Az önce çizdiğiniz labirent basit bağlantılıdır. Basit bağlantılı bir labirentte tüm duvarlar birbirine veya labirentin dış sınırına bağlıdır. Bu tarz bir labirentte sağ ya da sol elinizi bir duvara koyup, o elin duvarla temasını kaybetmeden yürürseniz eninde sonunda merkeze veya çıkış noktasına ulaşırsınız. Bu size en kısa yolu garanti etmese de bir biçimde labirentten kurtulmanızı sağlar.
Ancak çoklu bağlantılı labirentlerin birbirinden izole edilmiş bölümleri vardır. Bu sebeple bölümleri birleştiren bir duvar yoktur. Bu da yukarıda aktardığımız el yordamı ile yönünüzü bulma durumunu geçersiz kılar.
Trémaux’un algoritması
Merkeze ulaşamadan bir labirente girip kendinizi çıkmış veya aynı yolu defalarca yürümüş olarak bulabilirsiniz. Bu nedenle çeşitli labirentten kurtulma algoritmaları geliştirilmiştir. Bunlardan bir tanesi de Trémaux’un algoritmasıdır. Bu yöntem her durumda işe yaramaktadır.
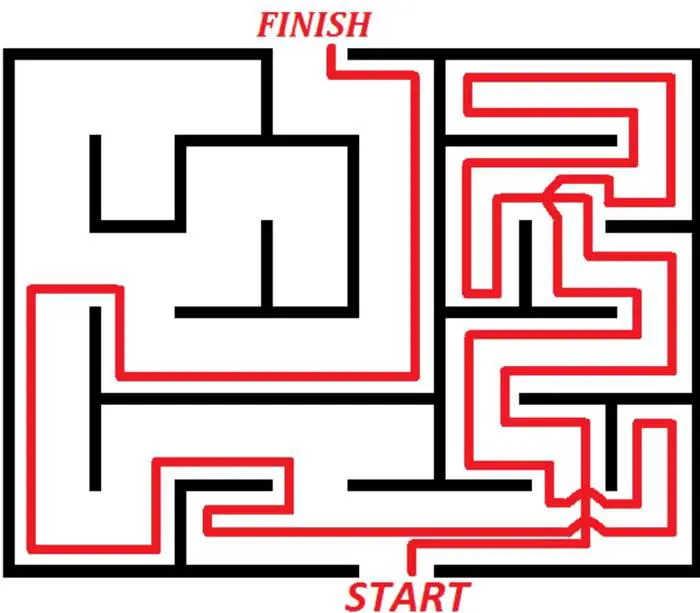
Charles Pierre Trémaux tarafından icat edilen Trémaux algoritması, bir labirentten çıkış yolunu bulmak için etkili bir yöntemdir. Bu algoritmanın tüm labirentlerde çalışması garantidir. Ancak en kısa rotayı bulması garanti değildir. Aslında bu algoritma hepimizin duyduğu Hansel ve Gretel masalını andırır ve uzun zamandır kullanılmaktadır. Yapmanız gereken labirentte ilerlerken arkanızda bir iz bırakmaktır. Algoritmayı basitçe özetleyelim.
Elinizde bir kalem olduğunu düşünelim. Öncelikle bir kavşaktan başlayarak, rastgele bir yol seçin. Kalemle de bu yolun başına ve sonuna bir işaret koyun ya da yol boyunca bir çizgi çekin. Başka bir kavşağa geldiğinizde, rastgele daha önce gitmediğiniz bir yol seçin ve ilerlerken yolunuzu çizmeye devam edin.
Önceden bir kez işaretlenmiş bir kavşağa varırsanız geri dönün ve yolunuzu ikinci kez işaretleyin. Ancak üzerinde iki işaret bulunan bir yola asla girmeyin. Bu biçimde yürümeye devam edin. Her durumda en az işaretli yollardan birini seçin (mümkünse sıfır, yoksa bir). Bu yolu takip edin ve işaretleyin.
Bu yöntem sonunda sizi labirentin her bir parçası boyunca iki kereden fazla yürümeden çıkışa götürecektir. Elbette bir labirentten çıkmak için kullanacağınız başka algoritmalar da vardır. Yazımızda bir tanesine daha yer verelim.
Pledge Algoritması
Bu algoritma temelde engelleri aşmak için tasarlanmıştır. Ancak duvar izlemenin işe yaramadığı bazı durumlarda başarılı olur. Algoritmada, başlangıçta keyfi bir yön (kuzey, güney, doğu, batı) seçilmektedir. Diyelim ki seçtiğimiz yön kuzey. Bu bizim referans noktamız olacaktır. Sonrasında engelle karşılaşıncaya kadar seçilen yönde ilerleyelim.
Karşınıza bir engel çıkınca yönünüzü kaydedin. Daha sonra engel sol tarafta olacak şekilde dönün. Şimdi sol elinizi duvara koyun ve yürümeye başlayın. Bu esnada dönüşlerinizi sayın. Toplam dönüş sıfır olunca yani başlangıçta seçtiğiniz yöne tekrar dönünce ilerlemeye devam edin. Bu algoritma aşağıda gördüğünüz biçimdeki tuzaklardan kolayca kaçmanızı sağlayacaktır. Ancak, labirentin içinde veya dışında yer alacak sabit bir noktayı bulmak için kullanılmaz.
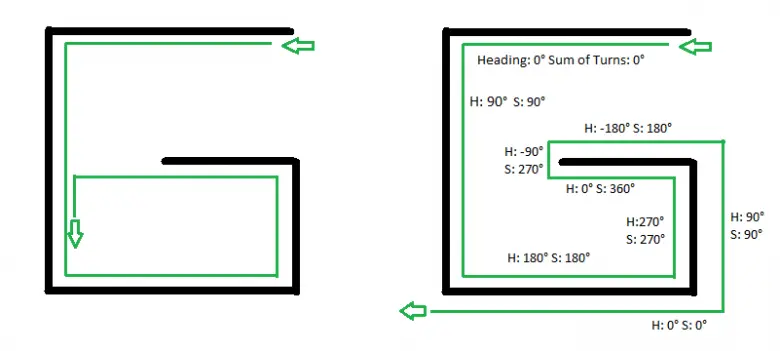
Bir labirentten çıkma söz konusu olduğunda aslında bu aktardıklarımızdan çok daha karışık bir çok algoritma vardır. Ancak bu tarz algoritmalar kullanım açısından daha az pratiklik taşımaktadır. Günümüzde bir çoğumuz günlük yaşantımızda bir labirentten kaçma sorunu ile uğraşmasak da bir bilgisayar programcısı için bu tarz algoritmalar ile uğraşmak rutin işlemlerden birisidir.
Kaynaklar ve ileri okumalar
- How to escape a maze – according to maths; Yayınlanma tarihi: 26 Ocak 2017; Bağlantı: https://theconversation.com
- Maze-solving algorithm; Bağlantı: https://en.wikipedia.org/
- The story of the Minotaur; Yayınlanma tarihi: 1 Mart 2001; Bağlantı: https://plus.maths.org/
Matematiksel










