Hepimiz lise matematiğinden ötürü integrali biliriz. S harfine benzeyen sembolüyle temelde bir tür toplamı ifade eder. Peki daha önce Feynman yol integralini duymuş muydunuz? Ünlü fizikçi Richard Feynman’ın ortaya koyduğu yol integrali (path integral) fizikçiler için kehanet formülüdür. Çünkü bu integral, gerçekliğimizin tüm olası sonuçların bir toplamı olduğunu söyler. Fakat bu nasıl olabilir?

Fizikçilere göre Feynman yol integrali, herhangi bir kuantum sisteminin davranışını tam olarak tahmin ediyor. Söz konusu bu kuantum sistemleri bir elektron, bir ışık ışını ve hatta kara delik bile olabilir. Nitekim yol integrali bugüne kadar o kadar çok başarı elde etti ki, fizikçiler bu integralin gerçekliğin kalbine açılan yol olduğuna inanıyor.
Yol integrali her ne kadar bu derece başarılı olsa da matematik olmaktan çok bir felsefedir. Çünkü başta da belirttiğimiz gibi bu integral, gerçekliğimizin olası tüm olasılıkların toplamı olduğunu söylüyor. Buna karşın bu toplamı nasıl yapmamız gerektiğine dair hiçbir şey söylemiyor.
Bu nedenle fizikçiler, on yıllardır konu hakkında yeni yaklaşımlar geliştirmeye çalışıyor. O yüzden bu yazımızda fizik, matematik ve felsefenin kesiştiği yerlerden biri olan Feynman yol integralini birlikte anlamaya çalışalım.
İşe En Az Eylem Prensibini Anlayarak Başlayalım
Bir sahilde cankurtaran olduğunuzu hayal edin. Etrafı gözlemlerken bir bakıyorsunuz birisi boğuluyor. En kısa yoldan boğulan kişinin yanına gitmeniz gerek fakat bir sorun var. Dümdüz kumdan koşarak mı gitmelisiniz yoksa kenardaki beton yoldan mı? Beton yol tam olarak boğulan kişinin olduğu yere gitmiyor. Fakat kumda koşmak da pek kolay değil, zaman alıyor. Bu durumda ne yaparsanız en kısa yoldan boğulan kişinin yanına gidebilirsiniz?
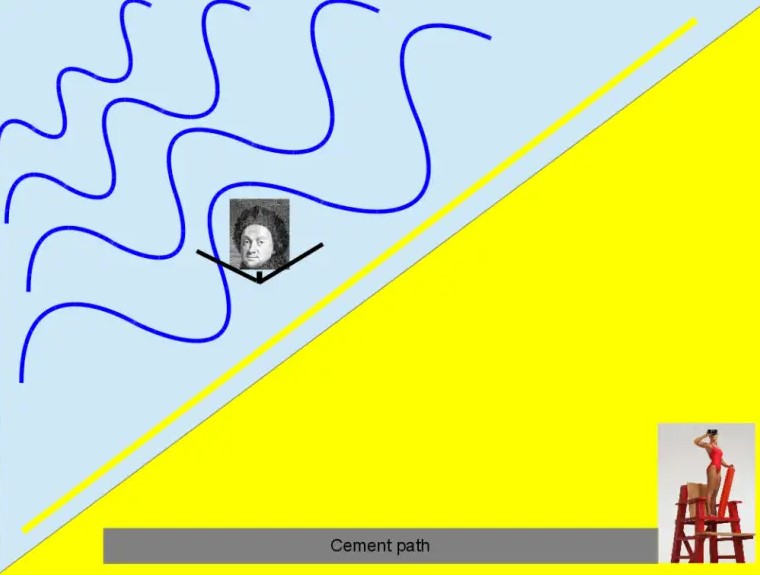
Aslında bu durumda en doğru tercih biraz kumda biraz da beton yolda koşmak olacaktır. Fakat bu noktada kumda ve beton yolda ne kadar koşacağınızı hesaplamak yerinde olacaktır. Çünkü bu sayede boğulmakta olan kişiye en kısa sürede ve en kısa yoldan ulaşabilirsiniz.
Peki bu olay size bir şeyler hatırlattı mı? Mesela lise fiziğinden bir şeyler. Eğer aklınıza optik konusundaki kırılma kuralları geldiyse tam isabet! Snell yasası ismini verdiğimiz bu kırılma kurallarıyla cankurtaran örneğimiz arasında bir benzerlik var.
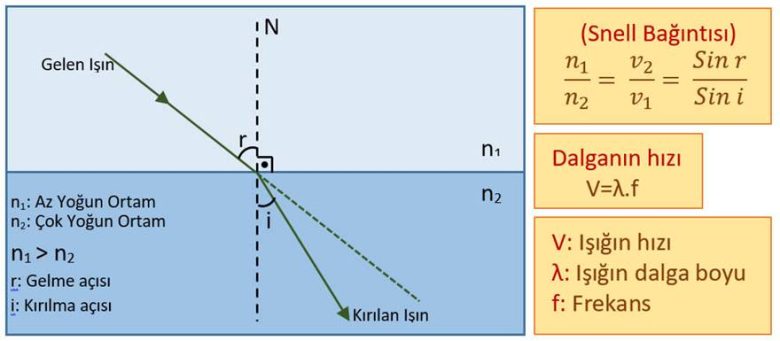
Snell yasası ve bizim cankurtaran hikayemizdeki ortak nokta, hem ışığın hem de cankurtaranın en kısa mesafeyi almak istemesidir. Fakat burada bir tuhaflık var. Cankurtaran en kısa mesafeyi kendisi isteyerek, kendi aklıyla seçti. Peki bir ışık ışını bunu nasıl yapıyor?
Bir foton en kısa mesafeyi alması gerektiğini nereden bilebilir ki? Elbette fotonun en kısa mesafeyi seçecek bir iradesi yok. Fakat fizikte en az eylem prensibi diye bir kavram var. Bir fotonun en kısa mesafeyi alma eğilimine en az eylem prensibi deniyor. Ve bu prensip, yazımızın konusu olan Feynman yol integralinin kalbinde yatan fikirdir.
Feynman Yol İntegrali Nedir?
Kuantum mekaniği 1926’da Erwin Schrödinger’in dalga fonksiyonunun zamana göre değişimi gösteren ve kendi adını taşıyan Schrödinger denklemini ortaya atmasıyla çığır atmıştı. Sonraki 10 yılda Paul Dirac da kuantum dünyasında alternatif bir vizyon geliştirdi.
Dirac’ın fikirleri bir şeyin A noktasından B noktasına en kısa yoldan gitmesini açıklayan en az eylem prensibinin genel anlamda en az enerji ve en az zaman harcayan versiyonuna dayanıyordu. Daha sonra Richard Feynman, Dirac’ın bu çalışmalarını keşfetti. Ve 1948’de Feynman yol integralini ortaya attı.

Klasik fizikte bir parçacık A noktasında B noktasına gideceği zaman iyi tanımlanmış tek bir yolu izler. Ancak kuantum mekaniğinde durum çok başkadır. Çift yarık deneyinden de hatırlayabileceğiniz üzere kuantum dünyasındaki bir parçacık aynı anda olası tüm yolları izler. Hatta bu duruma parçacığın süperpozisyon halinde olması denir. Süperpozisyonda bir parçacık, hem A noktasındadır hem B noktasındadır hem de iki nokta arasındaki yolu almaktadır. Kısacası tek bir pozisyonu veya durumu yoktur.
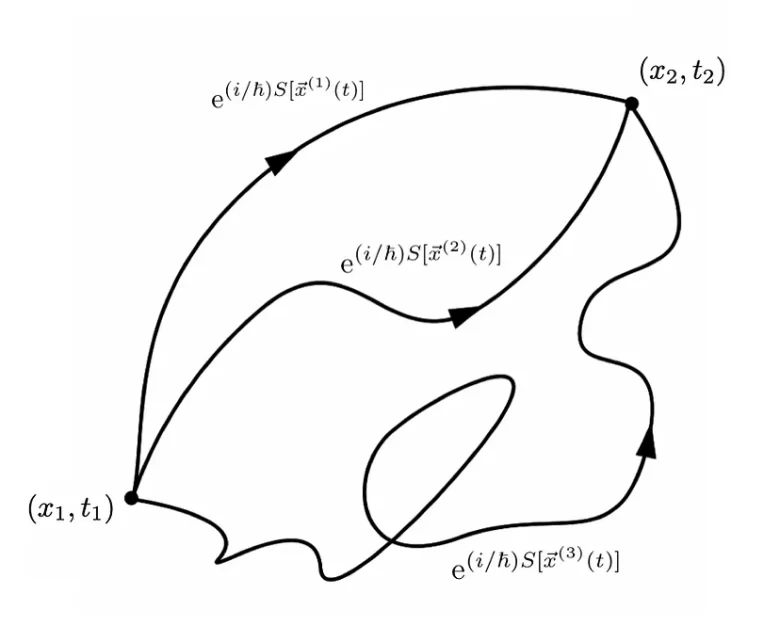
İşte Feynman yol integralinin dayanak noktası burasıdır. Parçacık mümkün olan tüm yolları aynı anda aldığından bunu yol integraliyle hesaplayabiliriz. Feynman yol integralinin denklemiyse şu şekildedir:
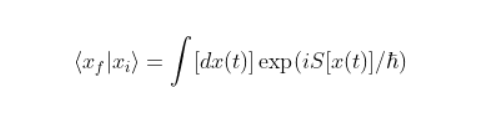
Burada |x_i⟩, parçacığın A noktasındaki başlangıç durumunu ve |x_f⟩, parçacığın B noktasındaki son durumunu temsil eder. S[x(t)] ise x(t) yoluna karşılık gelen eylemi belirtir ve ħ, Planck sabitini temsil eder. Exp(iS[x(t)]/ħ) karmaşık gösterimi, her bir yolun olasılığını temel olarak etkileyen bir niceliği temsil eder. [dx(t)]’li integral sembolüyse, dümdüzden dolambaçlıya kadar tüm olası yollar üzerindeki entegrasyonu gösterir.
Gerçekliğimiz Tüm Olası Gerçekliklerin Toplamı mı?
Az önce açıkladığımız Feynman yol integrali denklemi biraz kafa karıştırıcı gibi gelmiş olabilir. Sonuçta tüm olası ihtimalleri nasıl saptayıp nasıl hepsini toplayacağız öyle değil mi? Aslında bu noktada matematikçiler ve fizikçiler, sabit faz yaklaşımı adını verdikleri bir yönteme başvuruyor.
Fakat biz bu yönteme değinmeyeceğiz. Çünkü ileri matematik bilgisi içeriyor ve böylesi bir konuyu da basitleştirip özünden uzaklaştırarak anlatmayı tercih etmiyoruz. Eğer isterseniz sondaki kaynaklar kısmından sabit faz yaklaşımı yöntemi hakkında bilgi edinebilirsiniz.
Ancak yol integralini anlamaktaki tek sorun elbette bu değil. Aslında en bariz sorun, bu kadar ihtimalin nasıl birleşip tek bir gerçeklik haline geldiğidir. Yol integrali kabaca her olası yolu saptar ve her bir yolun genliğini hesaplar. Çıkan sayı size parçacığın o yolu alma olasılığının ne kadar olduğunu söyler. Daha sonra tüm olası yolların genliklerini toplayarak Feynman yol integralini hesaplamış olursunuz.
Bu noktada genliklerin karmaşık sayılar olması gerektiği önemlidir. Çünkü reel sayılar sayı doğrusunda bir nokta ile temsil edilirken, karmaşık sayılar vektör şeklinde temsil edilir. Ve vektörler konusundan hatırlayabileceğiniz üzere aynı yöne bakan vektörler birbirini güçlendirirken, zıt yöne bakanlar birbirini söndürür. Zaten Feynman yol integralinin en nihayetinde tek bir gerçekliğe varması da bu yüzdendir.
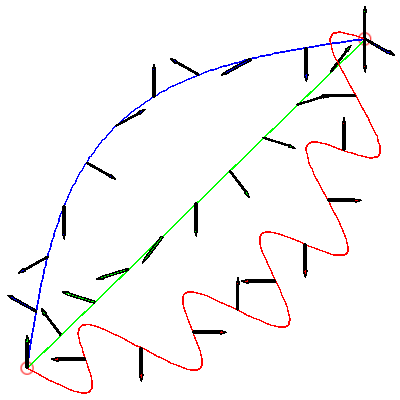
Bir parçacığın A ve B noktaları arasında dümdüzden dolambaçlıya kadar bir sürü yol alabileceğini söylemiştik. Dolambaçlı yollarda vektörler zıt yönlere baktığı için birbirlerini söndürür. Fakat düz yollarda vektörler aynı yöne baktığından birbirini güçlendirir. Bu da en nihayetinde düz yolun kaldığını bize gösteriyor. Bu sayede de tüm olası yollardan geriye bir tek klasik düz yol kalıyor. Yani tüm olası gerçekliklerin toplamı tek bir gerçeklik ediyor.
Sonuç Olarak;
Feynman yol integrali, başarılarıyla ve arkasında yatan fikirle bilim insanlarını büyülemeye devam ediyor. Fakat başta da belirttiğimiz gibi işin matematiği iyi çalışsa da yol integralinin anlamı hakkında pek az şey biliyoruz. Yine de bilim insanları bu integrali yeni çalışmalarla birleştirip yol integralinin özünü anlamaya çalışıyor.
Kaynaklar ve İleri Okumalar
- How Our Reality May Be a Sum of All Possible Realities ; Bağlantı: How Our Reality May Be a Sum of All Possible Realities | Quanta Magazine ; Yayınlanma tarihi: 6 Şubat 2023
- Exploring Feynman Path Integrals: A Deeper Dive Into Quantum Mysteries ; Bağlantı: Exploring Feynman Path Integrals: A Deeper Dive Into Quantum Mysteries | by Freedom Preetham | Quantum Mysteries | Medium ; Yayınlanma tarihi: 10 Temmuz 2023
- Reality Is—The Feynman Path Integral ; Bağlantı: Reality Is—The Feynman Path Integral (thephysicsmill.com) ; Yayınlanma tarihi: 16 Temmuz 2013
Matematiksel