Bir Futbol Topu Neden Beşgen Ve Altıgen Parçalardan Oluşur?

Top yuvarlaktır deriz ancak aslında, futbol topunun şekli yuvarlak değildir. Standart bir futbol topu, her beşgenin altıgenlerle çevreleneceği şekilde düzenlenmiştir. Yani 12 beşgen ve 20 altıgen olmak üzere 32 çokgenin birbirine dikilmesi ile yapılmıştır.

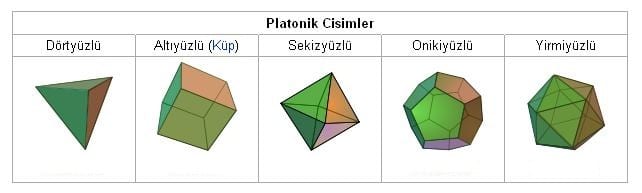
Ama neden beşgen ve altıgen? Bu sorunun cevabı günümüzden ziyade geçmişte, Platonik katıların geometrisinde yatmaktadır. MÖ 360 yıllarında Platon’un “Timaeus” adlı kitabında tanımladığı üzere düzgün, çokyüzlü (platonik) cisimler her köşesinde ay­nı sayıda birbirine eş düzgün çokgenin kesiştiği üç boyutlu cisimlerdir.

Bir Futbol Topunun Özel Şekli Matematikte Gizlidir

Bu tür çokyüzlülerin en küçüğü, 4 tepe nok­tası, 6 kenar ve 4 eşkenar üçgenden (4 üçgensel yüzden) oluşan düzgün dörtyüzlü piramit ve en büyüğü 20 üçgensel yüzden oluşan icosahedrondur. Bu cisimlerin neden tamı tamına beş tane olduğunun ispatında çok ilginç ve bir o kadar önemli bir formül kullanılmaktadır. Bu formülün adı “Euler’in çokyüzlüler formülü” olarak bilinmektedir.

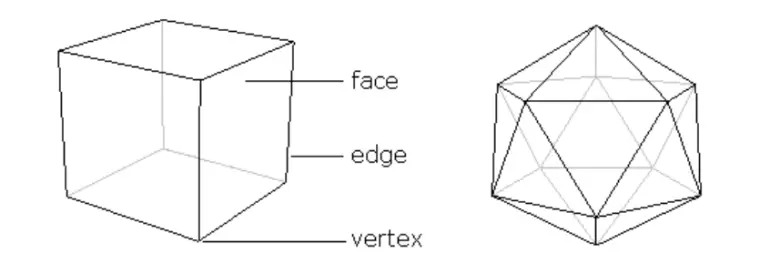
Şimdi yukarıdaki küp şekline bakın. Sahip olduğu köşelerin sayısını bulun ve bu sayıya V adını verin. Küpün 8 köşesi vardır, dolayısıyla V = 8 olacaktır. Ardından, sahip olduğu kenar sayısını bulun ve bu sayıya E adını verin. Bu durumda E = 12 olur.  Son olarak, yüzlerin sayısını sayın ve ona da F deyin. Küp için F = 6 biçimindedir.

Şimdi Euler’in formülü bize şunu söylüyor: V – E + F = 2. Yani köşe sayısı, eksi kenar sayısı artı yüz sayısı her zaman ikiye eşittir. Küp için, V = 8, E = 12 ve F = 6 olduğuna göre V – E + F = 8 – 12 + 6 = 14 – 12 = 2 sonucu doğrudur. Şimdi ise bu formülü futbol topumuza uygulayalım.

Topun Matematiksel Olarak Oluşturulması

Futbol topunun x sayıda altıgen ve y sayıda beşgenden oluştuğunu düşünelim. Toplam yüz sayısı x+y kadar olacaktır. Toplamda, beşgenlerin 5y, altıgenlerin de toplam 6x kenarı olacaktır. O zaman toplam kenar sayısı 6x+5y olmalıdır.

Her kenar, topu oluşturan iki yüz tarafından paylaşılır. Bu nedenle de bu sayının yarısı bizim şeklimizin toplam yüzünü verecektir. Yani (5x+6y)/2. Aynı mantıkla toplam köşe sayısını da hesaplayabiliriz. Ancak bir köşe üç şekil tarafından paylaşıldığı için toplam yüz sayısını bu sefer 3’e bölmemiz gerekir. Bu durumda toplam köşe sayımız da (5x+6y)/3 kadardır.

Şimdi bunları Euler formülünde yerlerine yazalım. Bu durumda çözümde y’ler birbirini götürecek ve x sayısı 12 olarak bulunacaktır. Artık futbol topumuz için 12 beşgen kullanılması gerektiğinden eminiz. Şimdi altıgen sayısını bulmamız gerekiyor. Bununla birlikte altıgen sayısında aslında bir sınırlama yoktur. Aynı şekilde tepe noktası sayısında da bir sınır yoktur.

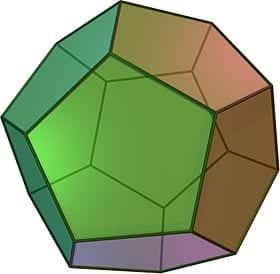
Ancak standart bir futbol topu için seçim yapılırken minimum değerler düşünülmüştür. Bu nedenle tepe noktası sayısı 60 olarak kabul edilmiştir. (Tepe noktalarında üç altıgen yan yana getirilemediğine göre, her tepe noktasında en az bir beşgen bulunmak zorundadır.

Toplam 12 beşgen olduğundan, topta en çok 60 tepe noktası var demektir.). Sonucunda, S = (5x+6y)/3 formülünde S yerine 60 ve x yerine 12 yazarsak altıgen sayısını veren y sayısı da 20 olarak elde edilecektir.

Futbol Topu da Zaman İçinde Değişti

Yaklaşık 40 yıl boyunca topun yapısı, klasik beşgen-altıgen 32 parçalı kaplama formatını takip etti; fakat 2006 yılında, tasarımda radikal değişiklikler yapıldı. 2006 yılında Almanya’da düzenlenen Dünya Kupası organizasyonunda kullanılan Teamgeist isimli top üzerinde yalnızca 14 kaplama parçası bulunuyordu.

Daha sonra Güney Afrika’da 2010 yılında düzenlenen aynı organizasyonda, 8 kaplama parçalı top ile tanıştık. 2014 yılında Brezilya’daki organizasyonda ise, Brazuca isimli top üzerinde yalnızca 6 kaplama parçası vardı.

Peki ama futbol topu tasarımı neden deyişti diye de sorabilirsiniz. Aslında, futbol topu üzerindeki kaplamaların tasarımı ve sayısı, topun havadaki hızını ve yönlendirilişini etkiliyor. Bu nedenle de çeşitli iyileştirmeler yapılıyor. Şu anda, 6 rakamının topun kaplaması için ideal rakam olduğu düşünülüyor.

Kaynaklar ve ileri okumalar:

• Kotschick, Dieter. (2006). The Topology and Combinatorics of Soccer Balls. American Scientist – AMER SCI. 94. 10.1511/2006.60.350.
• Football: aerodynamics of the perfect free kick; yayınlanma tarihi. 28 Haziran 2016; Kaynak site: Conversation. Bağlantı: https://theconversation.com/football-aerodynamics-of-the-perfect-free-kick-61700

Size Bir Mesajımız Var!

Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.

Matematiksel