Basit görünse de, Euler’in Çokyüzlü Formülü, matematikçileri 4000 yıldan fazla bir süredir büyüleyen, “çokyüzlü” dediğimiz üç boyutlu katıların temel bir özelliğini özetler. Bu formül ünlü İsviçreli matematikçi Leonhard Euler’in (1707 – 1783) adını taşır.

Çokyüzlü Nedir?
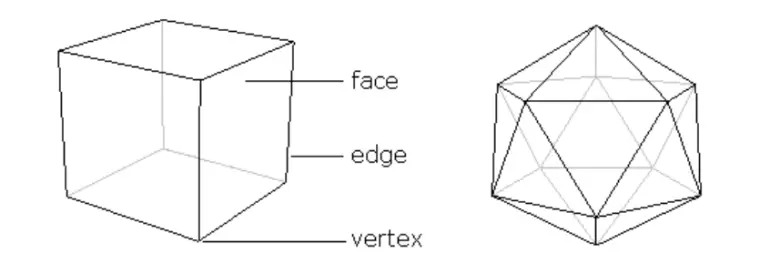
Çokyüzlü (Polyhedron), üç boyutlu bir geometrik şekildir. Yüzeyi, düz ve çokgensel yüzeylerden oluşur ve bu yüzeylerin kenarları düz çizgilerle birleşir. Çokyüzlü, tamamen kapalı bir şekildir, yani hiçbir açıklığı veya deliği yoktur. Çokyüzlü, tek bir parça halinde olmalıdır. Örneğin, yalnızca bir köşe veya kenarla birleşen iki ayrı parça, çokyüzlü olarak kabul edilmez.
Düzenli çokyüzlülere, Platonik Katılar denir. Bunlar, tüm yüzleri aynı türden düzenli çokgenlerden oluşan ve her köşesinde aynı sayıda yüzün buluştuğu simetrik, üç boyutlu şekillerdir. Bu katılar, matematikte ve doğada simetrinin en temel örnekleri arasında yer alır.
Platonik katılar, adını ünlü Yunan filozof Platondan alır. Platon, bu katıların evrenin temel yapı taşları olduğunu ileri sürmüş ve her bir katıyı bir elementle ilişkilendirmiştir. Ancak Platon’dan önce de bu şekiller Pythagoras ve Eudoxus gibi matematikçiler tarafından biliniyordu.
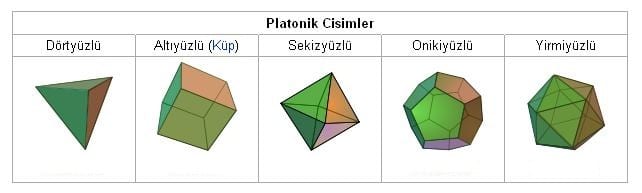
Platonik katılar yalnızca beş tanedir. Daha fazla Platonik katı olması mümkün değildir. Bu durum, Euler’in formülü ile kanıtlanır.
Euler Çokyüzlü Formülü Nedir?
Artık Euler’in formülünün çokyüzlüler hakkında bize ne söylediğini görebiliriz. Bir çokyüzlüye bakın, köşe sayısını sayın ve bu sayıya V deyin. Örneğin, küpün 8 köşesi vardır, yani V=8. Sonra çokyüzlünün kenarlarını sayın ve buna E deyin. Küpün 12 kenarı vardır, bu yüzden E=12. Son olarak, yüz sayısını sayın ve buna F deyin. Küp için F=6.
Şimdi Euler’in formülü bize şunu söylüyor: V – E + F = 2. Yani köşe sayısı, eksi kenar sayısı artı yüz sayısı her zaman ikiye eşittir. Küp için, V = 8, E = 12 ve F = 6 olduğuna göre V – E + F = 8 – 12 + 6 = 14 – 12 = 2 sonucu doğrudur.
İkosahedrona bakarsak, V = 12, E = 30 ve F = 20 olduğunu buluruz . Bu sayıları formülde yerine yazarsak V – E + F = 12 – 30 + 20 = 32 – 30 = 2 elde ederiz ki bu da doğrudur. Aslında bu formül, hemen hemen her çokyüzlü için doğrudur. İşe yaramadığı tek durum, aşağıdaki şekilde gösterildiği gibi içlerinde delikler olan şekillerdir.
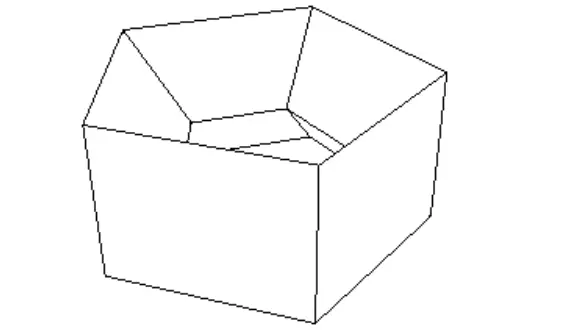
Euler’in formülü bize, örneğin, tam olarak yedi kenarı olan basit bir çokyüzlü olmadığını söyler. Bunu bulmak için karton, makas ve yapıştırıcı ile uğraşmanıza gerek yoktur. Euler formülünü benzer şekilde kullanarak, on yüzü ve on yedi köşesi olan basit bir çokyüzlü olmadığını da keşfedebiliriz.
Euler Çokyüzlü Formülü Neden Önemlidir?
Bu temel gözlemin matematiğin birçok alanıyla derin bağlantıları vardır, ancak Öklid, Arşimet ve Kepler gibi yüzyıllardır geometriyi inceleyen bilim insanları bunu anlayamamıştır çünkü sonuç geometriye bağlı değildir. Sadece şeklin kendisine bağlıdır: Topolojiktir.
Euler, çokyüzlülerin dışbükey olduğunu, yani herhangi iki noktayı birleştiren bir doğru parçasının şeklin tamamen içinde kaldığını varsaymıştı. Çok geçmeden, akademisyenler Euler formülünde dışbükey olmayan istisnalar buldular. Örneğin, 1813’te İsviçreli matematikçi Simon Lhuilier, bir çokyüzlüye daha çok donut şekli vermek için bir delik açarsak sonucun V – E + F = 0 olacağını fark etti.

Kilden bir çokgen yaparsak, kenarlarını bir keçeli kalemle işaretlersek ve onu bir top haline getirirsek, yüzler ve kenarlar eğri olur ancak sayıları değişmez. Bu nedenle, topolojik olarak küre olan herhangi bir şekil için Euler sayısı 2’dir; simit benzeri bir torus için 0’dır; düz bir disk için 1’dir. Euler formülünün bu topolojik anlayışı 1861’de Johann Listing tarafından bir makalede sunulmuştur.
Sonuç olarak
19.yy ortalarına kadar topoloji kendi başına bir araştırma konusu olamadı. 1904’te Henri Poincaré, Evrenin şeklini anlamak için topolojik bir temel oluşturmaya yardımcı olacak bir teori üreterek topolojiye somut bir gerçeklik kazandırdı. Tüm bunların öncül adımlarından birisi de Euler’in çokyüzlü formülü ile atılmıştı.
Kaynaklar ve ileri okumalar için:
- Euler’s polyhedron formula; yayınlanma tarihi: 25 Temmuz 2020; Kaynak site: Plus Math. Bağlantı: Euler’s polyhedron formula/
- Topology 101: The Hole Truth. Yayınlanma tarihi: 26 Ocak 2021. Kaynak site: Quanta magazine. Bağlantı: Topology 101: The Hole Truth
Matematiksel, matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel