Matematiğin en büyülü yönlerinden biri, karmaşık yapıların en basit kurallardan ortaya çıkabilmesidir. Buna güzel bir örnek Pascal Üçgenidir.

Pascal üçgeni muhtemelen tüm matematiksel diyagramların en ünlülerinden biridir. Bunun nedeni üçgenin oluşturulmasının basit olması ancak bünyesinde matematikçilerin ilgisini çekecek bir çok desen barındırmasıdır.
Pascal üçgenini oluşturmak için yan yana duran iki sayıyı toplamak ve sonucu alt satıra tam ortalarına yazmak yeterlidir. Bu biçimde üçgeni sonsuza kadar devam ettirebilirsiniz. Ancak üçgenin iki kenarı her zaman bir olmalıdır. Sayıları düzenlemek için bu kadar basit bir kuralın yalnızca basit sonuçlara yol açabileceğini düşünebilirsiniz. Ancak Pascal üçgeni cebir, sayı teorisi, olasılık ve kombinatorikler (sayma ve düzenlemenin matematiği) dahil olmak üzere matematiğin çeşitli dalları için verimli bir çalışma alanıdır.
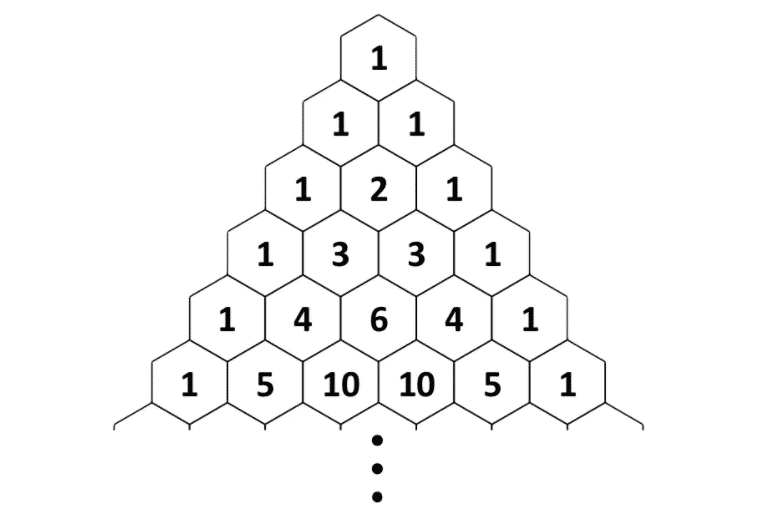
Pascal Üçgeni Farklı İsimler İle Bilinmektedir
Fransız matematikçi, filozof ve teolog Blaise Pascal, 17. yüzyılda üçgen hakkında kapsamlı bir çalışma yapan ilk kişi olduğu için genellikle, bu üçgen genellikle onun adı ile anılır. Blaise Pascal, özellikle, Fransız matematikçi Pierre de Fermat ile yazışmalarında olasılık teorisinin temellerini ortaya koymak için bu üçgeni kullanmıştır.

Bununla birlikte, İtalya’da bu üçgen adını matematikçi Niccolò Tartaglia’dan alır ve bu nedenle Tartaglia Üçgeni olarak bilinmektedir. Ancak Pascal ve Tartaglia’dan çok daha önce aslında bu üçgen farklı isimler altında bilinmekteydi. Bu nedenle de buluşu tek bir kişiye atfedilemez.
Erken dönem Hintli ve Çinli matematikçilerin, matematiksel serilerin toplamları için bu üçgeni kullandıkları bilinmektedir. Pascal üçgenine yapılan en eski referanslar ise MÖ 450 yılı civarında Hindistan’da ortaya çıkmıştır. Bu nedenle de Hintli matematikçiler üçgene Meru Dağı’nın merdivenleri der. Çin’de de Yang Hui’nin Üçgeni adı ile bilinmektedir.

Daha sonra, İslam dünyasından, İranlı şair, astronom ve matematikçi Ömer Hayyam da (1048–1131) bu üçgenin çeşitli özelliklerini araştırdı. Bu nedenle de Pascal üçgeni İran’da Hayyam’ın üçgeni olarak bilinmektedir.
Pascal Üçgeni ve Binom Açılımı İlişkisi
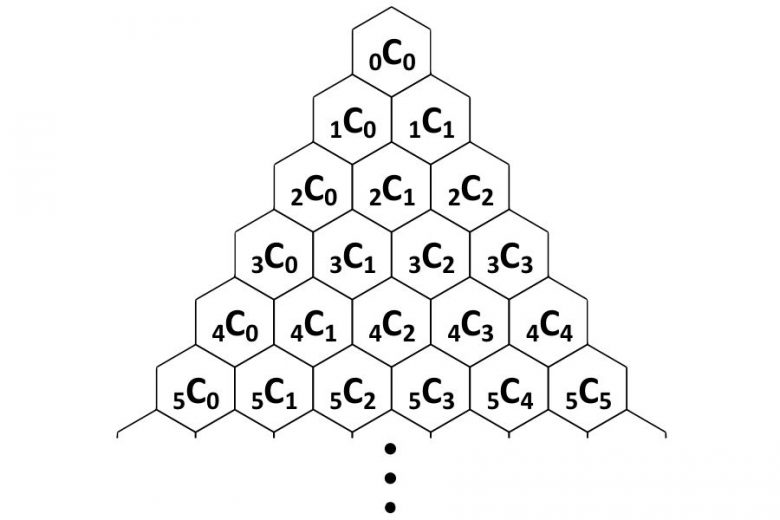
Pascal üçgeni aslında binom açılımı sonucunda ortaya çıkan ifadenin katsayılarının geometrik bir düzenlemesidir. Aslında binom açılımının katsayıları ile Pascal üçgenindeki sayılar arasındaki bu ilişki, sayılar ve olasılık hakkında temel bir gerçeği ortaya çıkarır.

Binom açılımı a + b gibi iki terimli ifadenin kendisiyle belirli sayıda çarpılması anlamına gelir. Yukarıdaki görselde açılımın katsayılarının Pascal üçgenindeki sayılar ile uyumlu olduğunu görebilirsiniz.
Kombinasyonlar
Pascal üçgeni, kombinatorik ile ilgili çalışmalarda doğal olarak ortaya çıkar. Bir poster hazırlamak için beş farklı renk kalem arasından üç kalem seçtiğinizi düşünelim. Bir posterde hangisinin kullanılacağını seçmek için renklerin seçildiği sıra önemli değildir. Eğer seçildiği sıra önemli olsaydı böyle bir duruma permütasyon denirdi. Bu durumda P( 5,3) biçiminde gösterilir. 5! / (5-3)! = 60 olarak hesaplanırdı.
Örneğimizdeki gibi sıralamanın önemli olmadığı durumlara kombinasyon denir. Olası kombinasyonların sayısı her zaman olası permütasyon sayısının bir kısmı kadardır. Bu durumda soru C(5,3) biçiminde olur ve 5! / [3! (5-3)!] = 5! / (3! × 2!) = 10 olarak hesaplanır. Bulduğumuz sonucun Pascal üçgeni ile olan ilişkisini aşağıdaki görselde inceleyebilirsiniz.
Binom Dağılımı
İki sonucu olan (yazı tura atma gibi) olasılıksal bir süreç için, sonuçların sırası matematikçiler ve istatistikçilerin binom dağılımı olarak adlandırdıkları şey tarafından belirlenir. Bu, Pascal üçgeni ile de ilgilidir. Üç defa bozuk para attığımızda 2 × 2 × 2 = 8 olası durum vardır. Bu olası durumlar arasında hepsinin yazı gelmesi 1, hepsinin tura gelmesi 1, iki yazı bir tura gelmesi 3 ve iki tura bir yazı gelmesi 3 biçimde olabilir. Bu sayılar Pascal Üçgeni ile eşleşmektedir.
| Atılan Para Sayısı | Olası Durumlar: Yazı ( Y) Tura (T) | Pascal Üçgenindeki Karşılığı |
| 1 | YT | 1 1 |
| 2 | YY,YT,TY,TT | 121 |
| 3 | YYY,YYT,YTY,TYY,TTY,TYT,YTT,TTT | 1331 |
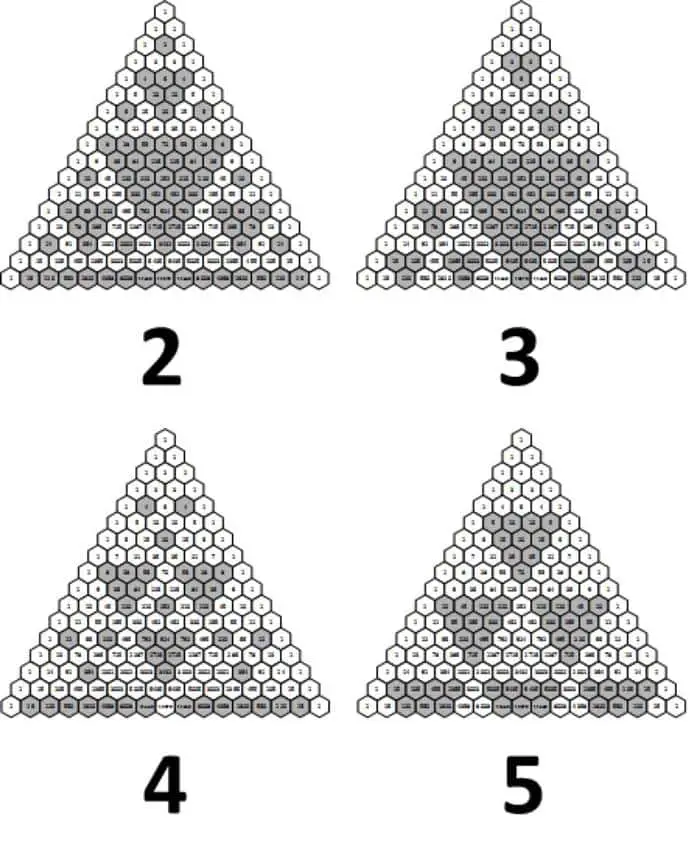
Pascal Üçgeni ile Sierpinski Üçgeni İlişkisi
Matematikçiler bu üçgenin içindeki sayıların örüntüsüyle ve özellikle bölünebilirliğiyle ilgilenir. Pascal üçgeninin sayılarının bölünebilirliğine göre renklendirilmesi, ilginç bir fraktal çeşidi üretir. Örneğin, ikiye bölünebilen tüm sayıların (tüm çift sayıların) renklendirilmesi sonucunda şekil Sierpinski üçgenine dönüşür.
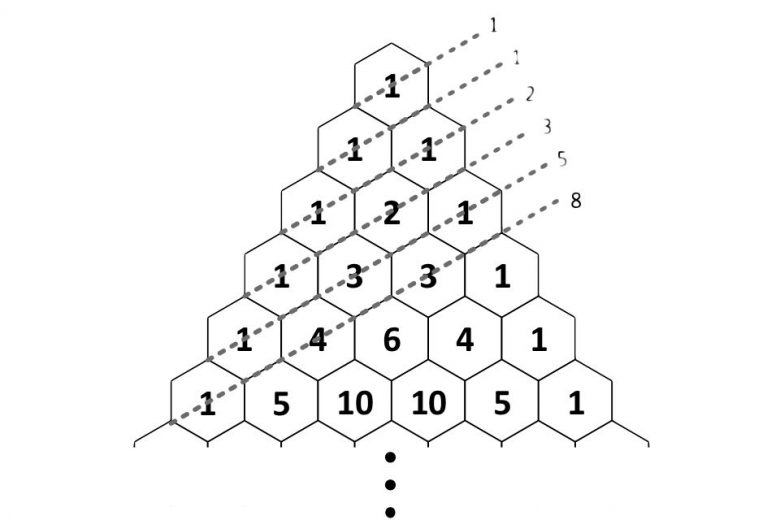
Pascal Üçgeni ve Fibonacci Sayıları
Ayrıca Pascal üçgenini kullanarak Fibonacci sayılarını da bulabilirisiniz. Fibonacci serisi ilk iki terimi 1 olan bir seridir. Bu serinin elemanları 1, 1, 2, 3, 5, 8, 13, 21, 34 biçiminde kendinden önceki iki sayının toplamına eşittir. Aşağıda da gördüğünüz gibi bu sayıları Pascal Üçgeninde bulmanız da mümkündür.
Üçgenin sayı teorisi ile olan bir başka bağlantısı, belirli bir satırın üstündeki satırlardaki tüm sayıların toplamının, her zaman verilen satırdaki sayıların toplamından bir eksik olduğunun keşfidir. Belirli bir satırın üstündeki tüm sayıların toplamı bir asal olduğunda, bu bir Mersenne asalıdır. Günümüzde bilinen en büyük asal sayıların büyük bir kısmı Mersenne asallarından oluşmaktadır. Pascal üçgeni yeterince büyük bir ölçekte çizebilseydik, bu sayıları üçgeninde bulmamız mümkün olabilecekti.
Kaynaklar ve ileri okumalar:
- Robert Coolman; Properties of Pascal’s Triangle; Yayınlanma tarihi. 17 Haziran 2015; Bağlantı: Robert Coolman; Properties of Pascal’s Triangle/
- The Math Book: Big Ideas Simply Explained, ISBN- 1465480242; DK Publishing
- The 12 days of Pascal’s triangular Christmas. Yayınlanma tarihi: 19 Kasım 2013. Kaynak site: The Conversation. Bağlantı: The 12 days of Pascal’s triangular Christmas
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










