Negatif sayılar bize yüzyıllarca zihinsel eziyet yaşattı ve bir çoğumuza halen yaşatmaya devam ediyor. Bu nedenle, negatif sayılardan kaçınmak için elimizden geleni yapıyoruz. Çünkü bir çok kişi hala iki negatif sayının hangisinin daha büyük olduğunu anlamakta bile zorlanıyor.

Matematiği öğretirken, öğretmenler problemleri açıklamak için birçok örnek kullanır. Başlangıçta bunların çoğu mantıklıdır. Ancak matematik eğitimi almaya devam ederseniz, yavaş yavaş sembolik kuralları ve önermeleri kabul etmek zorunda kalırsınız. Kafalar karışmaya başlasa da öğretmenler bu kuralların, daha ileri matematikte lazım olacağı için, öğrenilmesinde ısrar eder.
Yol boyunca, matematiksel kavramlar yavaş yavaş gerçeklikten ayrılmaya başlar. Öte yandan, eğer aynı zamanda fizik de okuyorsanız, her şey matematiğe bağlı gibi görünüyor. Peki ama, matematiğin kurallarını fiziksel olarak tanımlamamız olası değilse, nasıl oluyor da fiziksel fenomenlerin tanımı için matematik gerekli olabilir?
Cevap matematik tarihinde saklıdır. Matematiğin bazı kısımları sıradan deneyime karşılık gelirken bazı kısımları gelmez. Bazı matematiksel işlemlerin fiziksel işlemlere yakın bir benzerliği vardır, bazılarının yoktur. Örneğin −4 ×−4=16 çarpımını ele alalım. İki negatif sayının çarpımının pozitif bir sayı çıkmasının fiziksel olarak bir karşılığı yoktur.
Diyelim ki −4 ×−4=−16 olan bir sistem kurabilir miyiz? Aslında, evet yapabiliriz. Matematiksel mantıkçılar bunun doğru olabileceğini bilirler. Ancak biz sıradan insanlar bunu kullanmayız. Bizim için iki negatif sayının bir pozitif sayı çıkması fiziksel bir karşılığı olmayan kabuldür. Birçok insana “matematik yasalarını” değiştirmek imkansız gibi görünür. Ama gerçekte bu yapılabilir ve tarih boyunca farklı zamanlarda yapılmıştır.
Negatif Sayılar Hayatımıza Nasıl Girdi?
İnsanlığın negatif sayıların varlığını anlaması biraz da ticaretin gelişmesi ile ilgili gözüküyor. Antik dönemde Çinliler, hesap işlerini kolaylaştırmak için küçük bambu çubuklar kullandılar. Alacaklar kırmızı çubuklarla ve borçlar siyah çubuklarla gösterilmekteydi. Pozitif sayıların (kırmızı çubuklar) ve negatif sayıların (siyah çubuklar) kutuplaşmış doğası, Çin felsefesiyle de uyumluydu.
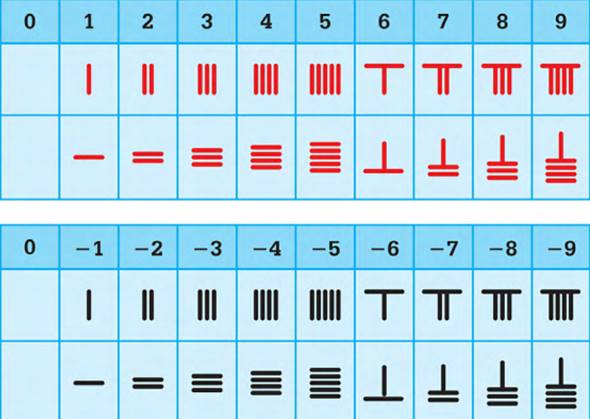
Birkaç yüzyıl sonra, Hindistan’da matematikçiler negatif sayılar ile ilişkili somut bir bağlam buldular. Bu elbette para idi. Sizden beş rupi ödünç alırsam, beş rupi borcum vardır. Ancak size beş rupi geri verdiğimde sıfır olacaktır. Yedinci yüzyıl gökbilimcisi Brahmagupta, pozitif ve negatif sayıların aritmetiği için “servet” ve “borçlar” adını verdiği kurallar yazdı. Bu sayede sıfır sayısı ile birlikte negatif sayılar varlığı da kabul görmeye başladı.
Ancak negatif sayıların sayı doğrusunda yerlerini alması oldukça uzun zaman aldı. Antik Yunan düşünürleri ve sonraki Avrupalı matematikçilerin çoğu, negatif sayıları saçma buldular. Sonucunda eksi bir elmayı hayal edemeyiz, bu yüzden doğuştan gelen bir negatif sayı hissine sahip olmamızın bir yolu yok. Bu düşünce 1600’lü yıllara kadar da devam etti.

Örneğin Fransız matematikçi Blaise Pascal’ın “0’dan 4’ü çıkarmanın sonucu nedir?” sorusuna verdiği yanıtı ele alalım. Ona göre cevap 0’dı ve aksini düşünen herkesi küçümsedi. René Descartes (1596-1650) negatif nicelikleri denklemlerin çözümü olarak kabul etti. Ancak bunlara gerçek sayılar yerine “yanlış kökler” adını verdi. Bilimsel keşif ve teknolojik yeniliklerin ortasında bile, Batı’nın en iyi beyinlerinden bazıları negatif sayıların varlığını kabul etmekte isteksizdi.
Negatif Sayıların Kabulü John Wallis Sayesinde Oldu
Oxford Üniversitesi’nde Geometri Profesörü olan John Wallis (1616-1703), insanların bir görselleştirme yapıldığında daha iyi düşündüklerini fark ettiğinde işler değişmeye başladı. John Wallis’in 1685 yılında yazdığı A Treatise of Algebra adlı çalışmasında negatif sayılar ilk defa sayı doğrusunda yerini almıştı.
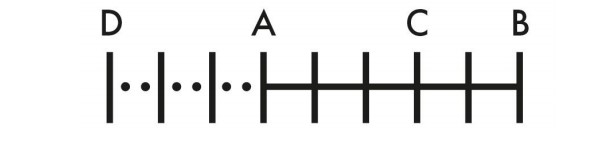
Bu sayı doğrusu aslında tüm zamanların en açıklayıcı diyagramıydı. Sizin de fark ettiğiniz gibi bu sayı doğrusunda negatif sayılar rakamlar yerine harfler ile gösteriliyor. Wallis’in bu rakamlardan kaçınmasının bir nedeni vardı. Sonucunda son derece önemli bir başka matematiksel araç – sıfır – henüz kabul edilmemişti. Matematik 1800’lerin ortalarına kadar, “nicelik bilimi” ve “büyüklük bilimi” ile eşanlamlı olarak tanımlandı. Bu nedenle, negatif sayılar “hiç yoktan az olan miktarlara” itirazlar olması olağandı.
Negatif Sayılar Nasıl Yazılır?
Negatif sayılar ilk kez sayı olarak kabul edildiğinde, bunların nasıl yazılacağı konusunda büyük tartışmalar yaşandı. 19. yüzyılın sonlarında, bazı yazarlar, negatif sayıların yatay olarak çevrilmiş pozitif sayılar olarak yazılması gerektiğini öne sürdüler.. Bir süreliğine sayıların üzerine ek bir çizgi eklenerek yazıldı. Bir dönemde de negatif ve pozitif sayılar ay ile gösterildi. Aşağıda bir örneğini görebilirsiniz.
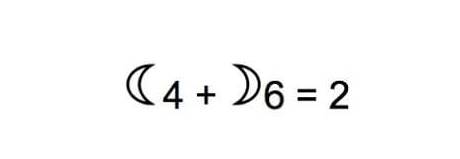
Negatif sayıların işleyişine ilişkin kuralların çoğu zaman içinde yaygın olarak kabul edilse de, bazı kuralların gerekçelendirilmesi konusunda da birçok anlaşmazlık vardı. Bunun en başında da negatif sayıların çarpılması ve bölünmesi geliyordu.
Leonhard Euler, 1770 tarihli Complete Introduction to Algebra (yıllardır en iyi cebir ders kitabı olarak kabul edilir) adlı eserinde, parasal varlıklar ve borçlar kavramlarına göre pozitif ve negatif niceliklerin önemini gösterdi.
Bu mantıkla, negatif bir sayının bir pozitif ile çarpımının negatif sayı yaptığı kuralını, birkaç kez alınan bir borcun hala bir borç doğurduğu gerekçesiyle haklı çıkardı. Ancak yine de 1796’ya kadar, matematik ders kitapları negatiflerin kullanılmasına karşı uyarıda bulunuyordu.
Negatif İki Sayının Çarpımı Neden Pozitiftir?
Pek çarpma kuralları ne olacak? Anlamak için sayı doğrusu bize yardımcı olacaktır. Diyelim ki 0 noktasında duruyorsunuz, sayı doğrusunun pozitif yönüne bakıyorsunuz. İki adım geriye gidiyorsunuz ve bunu 4 kez yapıyorsunuz. Bu durumda kendinizi -8 noktasında bulursunuz, bu da -2 adım çarpı 4’ün -8 olduğunu yani (-2)x4=-8 sonucunu bizlere gösteriyor.

Şimdi 0’a geri döndüğünüzü varsayalım, bu sefer negatif yöne bakıyorsunuz. 2 adım ileri gidiyorsunuz ve bunu 4 kez yapıyorsunuz. Bu sefer de -8 noktasında son bulursunuz, bu da 2 adım çarpı -4’ün yani 2x(-4)=-8 yaptığını bizlere gösterir.
Şimdi tekrar 0 noktasına geri dönün ve yüzünüzü negatif tarafa doğru çevirin. 2 adım geriye gidin ve bunu 4 kez yapın. Kendinizi 8 sayısında bulacaksınız. Geriye doğru adım atmak size -2 verir. Negatif yöne doğru bakmak size -4 verir. Bunun sonucunda da (-2)x(-4)=8 sonucunu elde ederiz.
Kaynaklar ve ileri okumalar
- Maths in a minute: negative numbers. Yayınlanma tarihi: 21 Ocak 2011. Kaynak site: Plus Math. Bağlantı: Maths in a minute: negative numbers
- From thousands to millions to billions to trillions to quadrillions and beyond: Do numbers ever end? Yayınlanma tarihi: 15 Nisan 2024. Kaynak site: Conversation. Bağlantı. From thousands to millions to billions to trillions to quadrillions and beyond: Do numbers ever end?
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





