Tartaglia olarak da bilinen Niccolò Fontana ve Gerolamo Cardano, kübik yani üçüncü dereceden denklemlerin çözümünde önemli rol oynadılar, ancak yol boyunca da düşman oldular.

İkinci dereceden bir denklemin köklerini bir formül yardımı ile günümüzde kolayca buluyoruz. Aslına bakarsanız bu kökleri neredeyse 3000 yıldır bulmayı biliyoruz. Peki ya üçüncü dereceden denklemler? Üçüncü dereceden denklemler, a≠ 0 olmak üzere, ax3 + bx2 + cx + d = 0 biçimindeki denklemlerdir. Matematikçiler bu denklemleri çok eski zamanlardan beri bilir. Peki onlar için de benzer formüller kullanmak mümkün müdür?
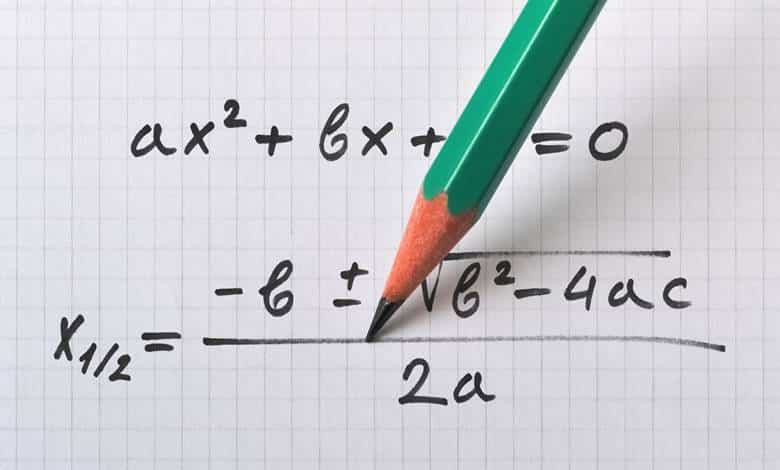
1494’te İtalyan Rönesans matematikçisi ve Leonardo da Vinci’nin arkadaşı Luca Pacioli Summa de Arithmetica isimli kitabını yayınladı. Bu kitapta, doğrusal ve ikinci dereceden denklemleri çözme yöntemleri yer alıyordu. Ancak kübik denklemleri çözmenin genel bir yönteminin bilinmediğini ve muhtemelen böyle bir yöntemin mümkün olmadığını da belirtmişti. Bu söylem, diğer matematikçileri bir çözüm bulmaya teşvik etti.
Tüm üçüncü dereceden denklemleri çözecek bir yöntem geliştirmek isteyen Ömer Hayyam konikleri kullanarak geometrik bir çözümü bulan ilk kişidir. Ancak kendisi genel bir çözüm bulmayı başaramamıştır. Üçüncü dereceden denklemlerin genel çözümlerinin bulunması hikâyesi de, matematik tarihinin en ilginç hikâyelerinden biridir. Hikâye Rönesans İtalya’sında geçer.
Üçüncü Dereceden Denklemlerin Genel Çözümleri Nasıl Bulundu?
1500’lerin başlarında, Scipio del Ferro adındaki Bolonyalı bir matematikçi, içinde x2 li terim içermeyen, diğer bir deyişle x3 + px = q biçimindeki kübik denklemleri çözmek için bir yöntem buldu.

Günümüzde, böyle bir keşif yapan bir matematikçi, onu yayınlamakta acele eder. Ancak, o dönemin İtalya’sında matematikçiler, çeşitli sorular ortaya atıp birbirlerine meydan okuyarak kendilerine bir geçim yolu bulmuşlardı. Matematiğe ilgili bir insan kitlesinin önünde yapılan bu gösterilerde seyirciler bahse girerlerdi. Bu düellolarda kazanan matematikçiler ise ortaya konan ödülleri kazanırdı.
Del Ferro bu nedenle yöntemini gizli tuttu. Bu sayede rakiplerinin çözemeyeceği soruları düelloda sorabilirdi. Sırrını iki öğrencisi Antonio Maria Fiore ve Annibale della Nave’ye ancak ölüm döşeğinde açtı. Ancak, etrafta del Ferro’nun keşfi hakkında söylentiler yayılmaya başlamıştı.

1530’ların başında, Tartaglia (italyanca’da kekeme) namı ile tanınan Niccolò Fontana adlı matematikçi de, kendisinin de kübik denklemleri çözebileceğini iddia etmeye başladı. Bunun üzerine Fiore, Tartaglia’yı bir yarışmaya davet etti. 30’ar adet soru ortaya atılmıştı ve hepsi de üçüncü dereceden denklemlerin belli bir formu şeklindeydi. Tartaglia hepsini çözerek düelloyu kazandı.
Yarışmayı duyduktan sonra ilginç yaşamı ve kumarbazlığıyla tanınan matematikçi Girolamo Cardano, yöntemi hakkında bilgi almak için Tartaglia ile temasa geçti. Cardano, o sıralar kapsamlı bir matematik kitabı yazmakla uğraşmaktaydı. Kitabına dönemin bu meşhur probleminin çözümünü de ekleyebilirse, bu eserin kendisine bolca ün ve para kazandırması gayet mümkündü.
Genel Çözümü İlk Kim Buldu?
Tartaglia ona çözümünü ancak bunu gizli tutmayı kabul ettikten sonra anlattı. Tartaglia çözümü ilk bulanan kendisi olduğunu düşünüyor ve bunu kitabında yayınlamak istiyordu.

Genel olarak üçüncü dereceden bir denklem ax3+bx2+cx+d=0 şeklindedir. Ancak Tartaglia’nın çözümü, bu genel formda değildi. Tartaglia’nın çözmek istediği denklem x3 + px = q biçiminde idi ve burada p ve q sayıları pozitif olmak zorundaydı. ( O dönemde negatif sayılar henüz yeterince kabul görmemişti.)
Cardano genel çözüm arayışına girdi. Önce üçüncü dereceden denklemleri 13 tipe ayırdı. Bunlardan ilk üçü Tartaglia’nın çözümünü verdiği denklem tipleriydi. Cardano bazı matematik hileleriyle diğer 10 denklemi bu 3 denkleme dönüştürdü. Böylece hepsini çözmüş oldu!
Cardano’nun dahi öğrencisi Ferrari
Bu esnada, Cardano’nun ev işlerine yardımcı olsun diye işe aldığı Lodovico Ferrari matematik çalışmalarını temize çekmeye başladı. Birlikte Bologna’ya yaptıkları bir gezide, Del Ferro’nun çalışmalarına rastladılar. Tartaglia ile aynı yöntemi kullandığını keşfettiler. Yani Tartaglia’dan çok daha önce, bu yöntemi bulan başka bir matematikçi vardı. Bu durumda yemin geçersiz olmuştu.
Cardano, matematik tarihinde önemli bir yeri olacak olan kitabı Ars Magna (Büyük Sanat) adlı eserini 1545’de yayınladı. Tartaglia’nın (ya da Del Ferro’nun) çözümü de kitapta yer alıyordu. Cardano çözümün kime ait olduğu konusunda yalan söylemiyor, her iki ismi de kitabında andı.
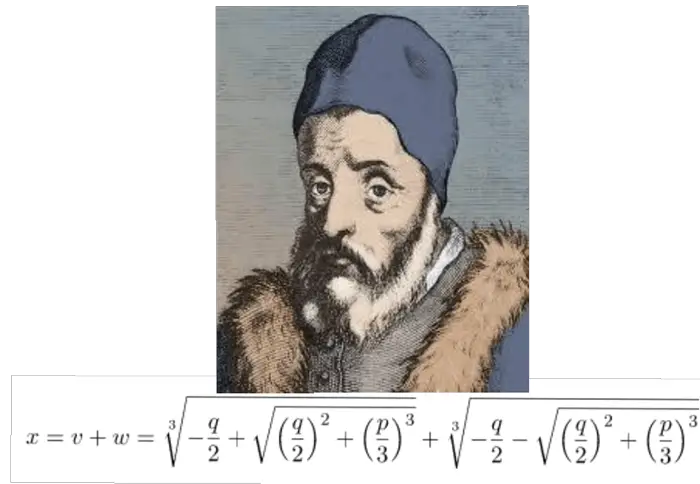
Cardano’nun kitabı kübiklerin çözümünü içermesi bakımından çok büyük ses getirmişti ve Tartaglia’nın itirazları çok da taraftar toplamamıştı.
Kübik çözümün formülünün günümüzde Cardano’nun formülü olarak bilinmesi size adaletsiz görünecektir. Ancak sadece Amerika’yı keşfetmek yetmez. Bu keşfi dünyanın geri kalanına da duyurmalısınız. Cardano bu son adımı tek başına attı ve zaferi elde etti.
Üçüncü Dereceden Denklemin Çözümü Nasıl Yapılır?
Üçüncü dereceden bir denklemin genel çözümü için aynı ikinci dereceden denklemlerde olduğu gibi discriminanta ( D) bakmak gerekir. D> 0 ise, üç farklı gerçek kök vardır. D = 0 ise, ya üç eşit gerçek kök (üçlü kök) ya da iki eşit kök (çift kök) ve bunlardan farklı basit bir kök vardır.
Tüm kökler gerçektir. D <0 ise, o zaman yalnızca bir gerçek kök vardır. Diğer iki kök, karmaşık eşlenik sayılardır. D=a2b2 + 18abc − 4b3 − 4a3c − 27c2 formülü ile hesaplanır.
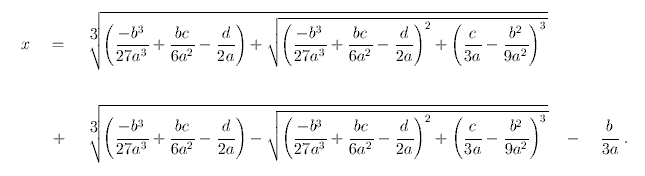
Kübik bir denklemle karşılaştığınızda, amaç her zaman var olacak bir gerçek kök bulmaktır. Ardından diğer iki gerçek kök polinom bölünmesi ve ikinci dereceden formülle bulunabilir. Pratik açıdan bakıldığında, tamsayı bir çözüm bulmayı başarırsanız, Cardano’nun formülünü kullanarak hesaplamalar yapmanıza gerek kalmaz. Tüm bunlar ne işe yaradı derseniz…
Üçüncü dereceden denklemlerin genel çözümlerinin bulunması karmaşık sayıların varlığını anlamamız ve geliştirmemiz açısından önemli bir adımdı. Sadece günümüz matematiği değil, aynı zamanda günümüz fiziği de hayali sayılar olmadan düşünülemezdi. Cardano’nın başarısı tahmin ettiğinden çok daha öteye gitmeyi başarmıştı.
Kaynaklar ve ileri okumalar:
- Saiber, Arielle. (2014). Niccolò Tartaglia’s poetic solution to the cubic equation. Journal of Mathematics and the Arts. 8. 10.1080/17513472.2014.933552.
- The Sordid Past of the Cubic Formula. Yayınlanma tarihi: 30 Temmuz 2022. Kaynak site: Quanta Magazine. Bağlantı: The Sordid Past of the Cubic Formula
- The Cubic Equation as Poetry; yayınlanma tarihi: 21 Nisan 2016; Bağlantı: https://blogs.scientificamerican.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










