Matematikçilere en beğendikleri formülü sorduklarında alınan cevap genellikle Euler Formülü olur. Bu formülden fizikçi Richard Feynman’ın derslerinde “matematiğin en dikkate değer formülü” olarak bahsettiği de bilinmektedir. Gerçekten de bu formül hem fiziğin hem de matematiği kalbinde yer alır. Peki ama neden önemlidir?
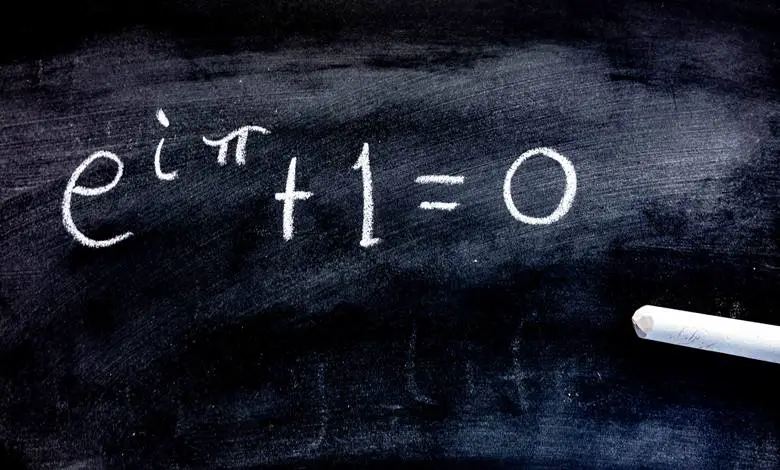
Matematikteki birçok şey, muhtemelen tüm zamanların en üretken matematikçisi olan Leonhard Euler’in adını almıştır. Yukarıda gördüğünüz bu denklem de onun adını taşır ve üstel fonksiyonların, sanal sayıların ve trigonometrinin görünüşte ilgisiz dünyalarını estetik açıdan hoş tek bir denklemde zarif bir şekilde birleştirir.
Ayrıca matematikte sıklıkla kullandığımız beş tanıdık sayıyı (e, i, π, 0 ve 1) ve üç basit işlemi (üs, çarpma ve toplama) bu denklemde birlikte görürüz. Matematiğin görünüşte farklı dallarını son derece basit bir şekilde birbirine bağladığı için de “matematiğin en güzel formülü” olarak kabul edilir. Ancak bu tam olarak neden önemli olduğunu bize açıklamaz.

Günümüzde adı Euler ile eşleşen o kadar çok formül vardır ki kimi zaman bunlar birbirine kolaylıkla karışabilmektedir. Bizim bu yazıda ele alacağımız Euler formülü üstel fonsiyon ve trigonometriyi birleştirmesi açısından önemlidir. Aslına bakarsanız matematiğin en güzel formülünün adı Euler özdeşliğidir. Euler özdeşliği Euler formülünün özel bir durumudur.
Euler Formülü Nedir?
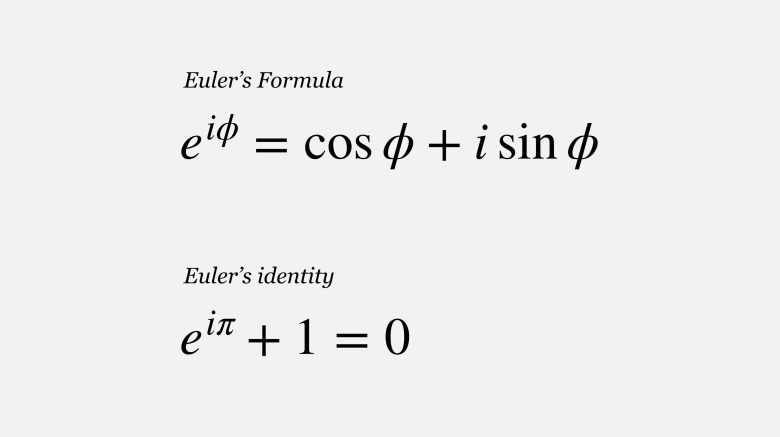
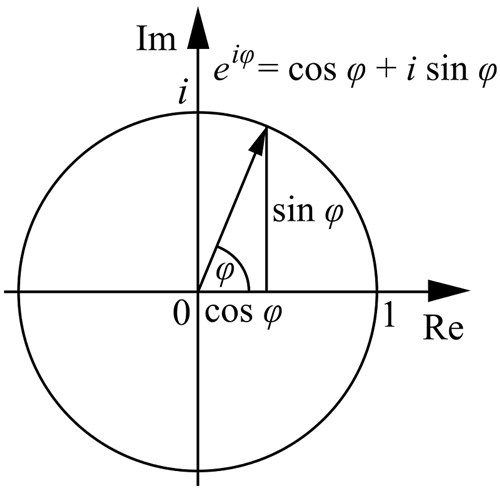
Euler formülü trigonometrik fonksiyonlar ile üstel fonksiyonlar arasındaki temel ilişkiyi kurar. Geometrik olarak, bir karmaşık sayının iki gösterimi arasında köprü kurmanın bir yolu olarak da düşünülebilir. Aşağıda gördüğünüz herhangi bir r uzunluğuna sahip olan doğrunun koordinat düzleminde gösterilişidir.
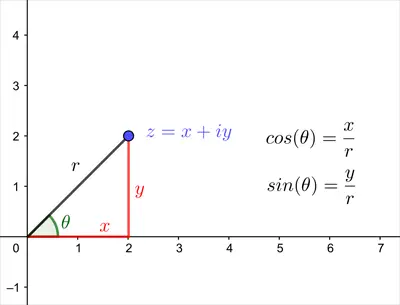
Bu sayede düzlemdeki bir (x,y) noktası, kutupsal koordinatları ile de tanımlanabilir. Bunu yapmak için yukarıdaki oranlardan x ve ye değerini hesaplamak ve sonuçlarını z=x+iy karmaşık sayımızda yerlerine yazmak yeterli olacaktır.
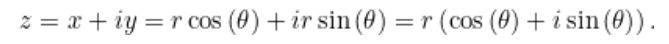
Ancak daha işimiz bitmedi. Düşüncenin güzelliği aslında burada karşımıza çıkıyor. Aşağıda kosinüs, sinüs ve üstel fonksiyonların kuvvet serileri verilmiştir. (Nereden geldikleri konusunda endişelenmeyin; sadece görünümlerine bakın)
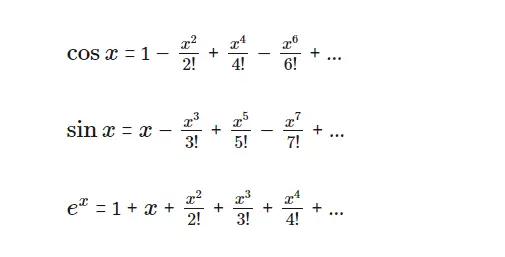
Yukarıdaki üçlüye dikkatle bakarsanız üstel fonksiyonun kuvvet serisi ve sinüs ile kosinüs fonksiyonları arasında bir ilişki olduğunu fark edeceksiniz. İşte bu ilişki Leonhard Euler’i matematik tarihindeki en muhteşem ve en geniş kapsamlı formüllerden birini keşfetmeye yönlendirdi.
Bu noktadan sonra bir adım daha atarak bizi matematiğin en güzeli olarak tanımlanan denkleme ulaşabiliriz. Bunun için yapmamız gereken tek şey açının yerine 180° veya π radyan yazmak olacaktır.
Euler Formülü Ne İşe Yarar?
Şu ana kadar bulduklarımız size pek bir işe yaramayacak gibi gözükecektir. Ancak aslında pratik de öyle değildir. Euler formülü döngülerin ve dalgaların somutlaşmış hali olan sinüs ve kosinüslerin, büyüme fonksiyonları olarak da bilinen üstel fonksiyonun gizli akrabaları olduğunu bizlere gösterir. Doğrudan sonsuz serilerden türetilen Euler formülü elektrik mühendisliği, kuantum mekaniği ve dalgalar ile ilgili tüm teknik disiplinlerde vazgeçilmezdir.
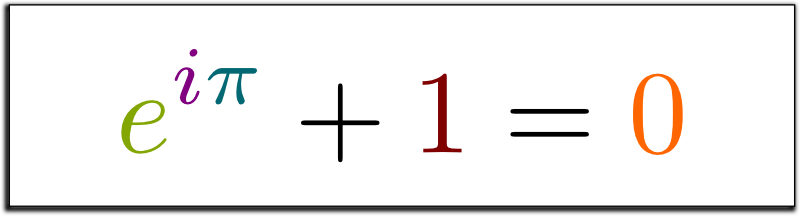
Dip Not: Euler, formülünün e sayısını cos ve sin terimleriyle ilişkilendirdiğini birçok yerde belirtmiştir. Ancak Euler’in kendi adına atfedilen özdeşliği bulduğuna dair somut bir kanıt bulunmamaktadır. Bazı kaynaklar bu özdeşliğin Euler’in doğumundan önce kullanılmakta olduğunu öne sürmektedirler. Bu durum da aslında Stingler kanununa bir örnektir.
Kaynaklar ve ileri okumalar:
- How Infinite Series Reveal the Unity of Mathematics. Yayınlanma tarihi: 24 Ocak 2022. Kaynak site: Quanta Magazine. Bağlantı: How Infinite Series Reveal the Unity of Mathematics
- Euler’s Identity: ‘The Most Beautiful Equation’. Yaınlanma tarihi: 1 Temmuz 2015. Bağlantı: Euler’s Identity: ‘The Most Beautiful Equation’
- Euler’s formula; Yayınlanma tarihi: 6 temmuz 2021; Bağlantı: https://plus.maths.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel



