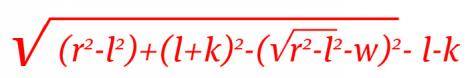Giderek artan araç sayısının beklendik sonucu, trafikte harcanan daha fazla zamandır. Bunu göze alsanız bile diğer bir sorun ise park etmek istediğiniz zaman karşınıza çıkacaktır. Sonucunda bir çok kişi otopark bulma sorunu neticesinde aracını yol kenarına yola paralel biçimde park etmek zorunda kalır. Bu da beraberinde başka sorunları getirir.

Neyse ki matematikçiler bu konuya da el atmış durumda. Aşağıda okuyacağınız iki ayrı araştırma araç park etmenin de aslında bir matematik hesaplaması olduğunu ortaya koyuyor. Önce araç park etme formülünü öğrenelim. Sonrasında da doğru otopark düzenlemesinin nasıl olması gerektiğini. Hazırsanız başlıyoruz.
Araç Park Etme Formülü
Arabanızı park etmek istiyorsunuz ve şans eseri boş bir yer buldunuz. Yol manevra yapmak için yeterince geniş gözüküyor. Ama iki arabanın arasına park etmek için yeterli alan olup olmadığından emin değilsiniz. İşte bu noktada, matematik işinize yarayacaktır.
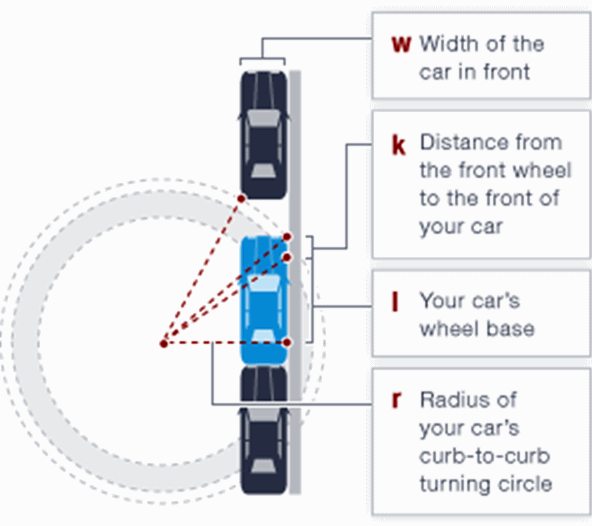
Mükemmel paralel park etme formülü Londra Üniversitesi matematik profesörlerinden Simon Blackburn’ün çalışması idi. Formüldeki uygun uzaklık ölçülerini gerekli yerlere girerseniz aracınızın boşluğa sığıp sığamayacağını anlıyorsunuz. Pratikte bu formülün uygulanabilirliği pek olası gözükmese formül aşağıda verildiği gibi…
- r: Aracınızın dönüş alanı üzerinden çizilen bir yarıçap
- l: Tekerleklerin açıklığı
- k: Aracın tekerlekleri ile ortası arasındaki mesafe
- w: Arkanızda olan aracın genişliği
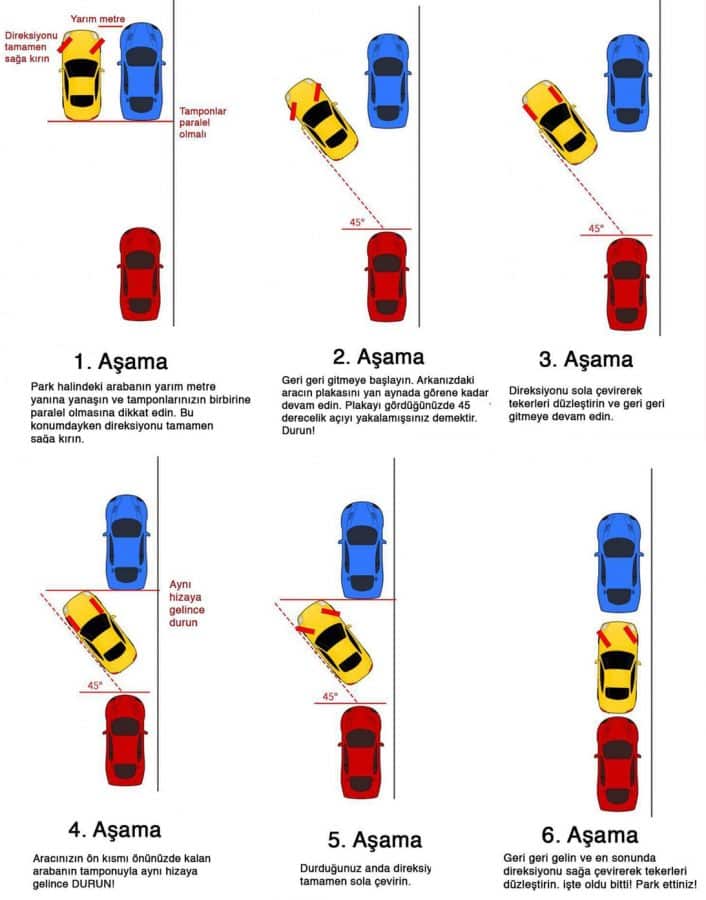
Aslında bu formül tam olarak ne kadar ekstra boşluğa ihtiyacınız olduğunu söylemekle kalmıyor. Aracınızın uzunluğuna bağımlı olmadan basit park etmenin aşamalarını da anlatıyor. Aşağıdaki görsele bakarak, araç park etmemiz gerektiğinde geometrinin biz farkında olmadan işin içine karıştığını görebilirsiniz. Şimdi ise araç park etme sorunumuz için matematikçilerin bir başka önerisini içeren ikinci araştırmaya geçelim.
Yetersiz Park Yeri Sorunu
Araçlarımızı toplu bir biçimde park etmek zorunda kaldığımız zamanlarda genelde önümüzdeki aracı park etmesini beklerken, gereksiz biçimde zaman kaybederiz. Bir profesör, boşlukların açısı, trafik akışının yönü ve hatta binanın şekli dahil olmak üzere mükemmel bir park yerinin arkasındaki matematiği ortaya çıkardı. Salford Üniversitesi’nde matematik profesörü olan David Percy’ye göre, ızgara tabanlı otoparklar en verimli tasarım değil.

Genelde park yerlerini birbirinden ayıran çizgiler 90 derecelik açıyla çizilidir. 90 derecelik açıyla aracınızı park yerine yerleştirirseniz, çıkış esnasında geri gitmek için arka planda aracınızın uzunluğu kadar boşluk bırakılması gereklidir. Bunun anlamı aslında park yerindeki boş alanların israfıdır. Ancak 45 derecelik açıyla yerleştirilen bir araba çok rahat bir şekilde daha dar bir boşlukta geri vitesle manevra yapıp çıkacaktır. Bunun sonucunda da park alanından tasarruf edilmiş olur.
Percy’ye göre 45 derecelik park yerleri park alanında %23′ lük bir kazanım sağlıyor. Bu da 500 arabalık bir park yerine 119 araba daha fazla aracın park etmesi anlamına gelmektedir. Bu iki örnek matematiğin hayatımızı kolaylaştırmak adına iş başında olduğuna sizleri inandıracaktır. Yazının devamında göz atmak isterseniz: Braess Paradoksu: Daha Fazla Yol Daha Az Trafik Demek Değildir!
Kaynaklar ve ileri okumalar için:
- Mathematician solves the puzzle of the perfect parking lot – and says leaving your car at an angle is key; Yayınlanma tarihi: 25 Ağustos 2016; Bağlantı: https://www.dailymail.co.uk/
- Here’s what maths can teach us about how to design the perfect car park; Yayınlanma tarihi: 26 Eylül 2016; Bağlantı: https://theconversation.com/
- The Formula For Perfect Parallel Parking. yayınlanma tarihi: 23 Ocak 2010; Bağlantı: https://www.npr.org/2010/01/23/122880263/the-formula-for-perfect-parallel-parking
- Cherif, Abour & Stamati, Angeliki. (2018). Learning Mathematics in Car Parking Lots: A Case for Promoting STEM Education Learning Activities.
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel