Yeni yollar inşa etmek trafik sıkışıklığını artırır. Ayrıca mevcut yolların kapatılması ise trafik sıkışıklığını azaltır. Tamamen sezgilerimize aykırı olan bu durum kanıtlanmıştır ve günümüzde Braess Paradoksu olarak bilinmektedir.

Şimdi bir senaryo düşünelim. Sabahtan akşama trafik sıkışıklığı ile boğuşmak zorunda kaldığınız herhangi bir metropolde yaşamak zorunda olun. O sıralarda da bu metropole yeni bir belediye başkanı seçilsin. Bu başkan da bir biçimde tanıdığınız olsun. Bir gün sizinle konuşurken şu cümleleri söylesin.
“Şehrimde yeni yollar inşa etmek için bir milyar dolara kadar harcayabilirsin. Bana nerede ve nasıl olduğunu söyle, projeni finanse edeyim.” İşte o zaman yapmanız gereken 1968’de Alman matematikçi Dietrich Braess tarafından öne sürülen ve bu durumda yapılması gereken en iyi şeyin yeni yol yapmak değil mevcut yolları kapatmak olduğunu söylemeniz gerekir. Başkanın tepkisinin ne olacağını bilemeyiz ancak matematik açısından çözüm budur.

Bu paradoks, her sürücünün kendi seçiminin diğer sürücüler üzerindeki etkilerini dikkate almadan en hızlı rotayı seçmesi nedeniyle ortaya çıkar. Bu paradoksun arkasındaki mantığa daha yakından bakmak için aşağıda gösterilen durumu düşünün.
Braess Paradoksu Nedir?
Bir yolculuğun Başlangıç ve Bitiş olarak etiketlenmiş iki büyük şehir olsun. İki şehir arasındaki yolcuların iki rota seçeneği vardır: A Kasabası üzerinden veya B Kasabası üzerinden arabalarını sürebilirler.
Başlangıçtan A Kasabasına ve B Kasabasından rotanın sonuna giden yolların her ikisi de otoyoldur. Bu yollarda herhangi bir sayı da araç yolculuk yapabilir ve yolu tamamlamak 105 dakika sürer. Ancak başlangıçta A kasabasına ve B kasabasından bitişe kadar olan yollar ise küçük dar yollar. Bu yollarda yolculuk için geçen süre ise yolda N tane araba varsa her araç için N dakikadır.
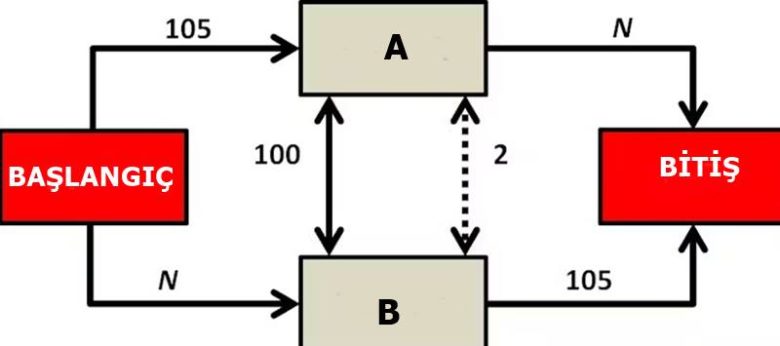
A Kasabasını B Kasabasına bağlayan ve yolculuk süresi 100 dakika süren eski bir yol da var. Bu yol o kadar yavaş ki, başlangıçtan bitişe kadar hiçbir araç sürücüsü bu yolu içeren bir rotayı seçmeyecektir. Eğer 100 arabanın aynı anda baştan sona kadar seyahat ettiğini varsayarsak, o zaman A ya da Kasabasından geçmenin bir farkı yoktur.
Sonucunda tüm araçlar trafikte aynı zamanı harcayacaktır. Bu durumda trafik yaklaşık eşit olarak bölünecektir. Yani bu durumda ağdaki ortalama seyahat süresi kabaca 155 ( 105+100/2) dakikadır. Bu en hızlı rotadır. (Gerçekte, arabaların iki yola eşit bölünmesi elbette olası değildir. Ancak önemli bir dengesizlik olmadığı ağdaki ortalama seyahat süresi 155 dakika olacaktır.

Şimdi, A Kasabası ile B Kasabası arasındaki yolun iyileştirildiğini düşünelim. Bunun sonucunda kasabalar arasında yolculuk 100 dakika yerine artık yalnızca 2 dakika sürüyor. Artık en hızlı rota, tüm sürücülerin başlangıçtan B Kasabasına 100 dakikada gitmesi sonrasında A Kasabasına 2 dakikalık yolculuk yapması ve ardından A Kasabasından sona kadar 100 dakika daha gitmesi biçiminde. Bu yolculuk toplamda 202 dakika sürüyor.
Ancak bu sonuç, ilk durumdan 47 dakika daha uzun. A Kasabası ile B Kasabası arasındaki eski yol son derece verimsiz olsa da, bu verimsizlik aslında ağın bir bütün olarak makul derecede verimli kalmasını sağlıyordu. Sonucunda bu yol trafiğin ikiye bölünmesini sağlıyordu. Ancak bu nispeten önemsiz yolun iyileştirilmesi, trafiğin eşit biçimde dağılmasını engelledi ve sonucunda da genel sistemi iyileştireceğine kötüleştirdi.
Braess Paradoksu İle İlgili Örnekler
Bu paradoks basit bir matematiksel tuhaflık değildir. Yeni yollar inşa etmek yerine yolların kaldırılmasının ulaşım ağlarını iyileştirdiğine dair çok sayıda örnek vardır.

1990’da New York’ta çok yoğun bir şehirlerarası yol olan 42. caddenin kapanmasının bir trafik kabusuna neden olması bekleniyordu. Bunun yerine, 25 Aralık 1990’da The New York Times’ta bildirildiği gibi, trafik akışı gerçekten iyileşti. 2005 yılında, Seul’de altı şeritli bir otoyol kaldırıldı. Sonrasında çevresel faydaların yanı sıra şehir genelinde trafikte bir hızlanma olduğu görüldü.
1960’ların sonlarında Stuttgart şehri, şehir merkezindeki trafiği hafifletmek için yeni bir cadde açmaya karar verdi. Ancak bu cadde trafiği daha kötü hale getirdi, sonrasında da yetkililer kapatmak zorunda kaldı. Yakın zamanda yapılan deneysel bir çalışma da, yol kapasitesinin arttırılmasının herkes için daha kötü trafik koşullarına yol açabileceğini göstererek bu paradoksun hala mevcut olduğunu doğruladı
Braess paradoksu sadece trafik için geçerli değildir ve birçok bağlamda ortaya çıkar. Örneğin, 2012 tarihli bir makalede, Max Planck Enstitüsü’ndeki bilim insanları, bir enerji şebekesine güç hatları eklemenin şebekenin performansını mutlaka iyileştirmeyeceğini ortaya koydu. Yeni hatlar, mevcut hatlara göre nerede bulunduklarına bağlı olarak sonucu daha verimsiz hale de getirebiliyordu. Daha az hat bazen daha verimli bir elektrik şebekesi demek olabiliyordu.
Sonuç olarak
Trafikte bunaldığınız zamanlarda daha fazla değil, daha az yola ihtiyacınız olduğunu anımsayın. Bu paradoksun nedeninin bencilce hareket eden sürücüler olduğunu unutmayın. Aslında bu durum ekonomide de kendine bir yer edinmiştir.
Kaynaklar ve ileri okumalar için:
- Raphael Rosen; From Klein Bottles to Chaos Theory, a Guide to the Nerdiest Math Facts, Theorems, and Equations; 2015
- Do more roads really mean less congestion for commuters?. Yayınlanma tarihi: 12 Nisan 2015. Kaynak site: Conversation. Bağlantı: Do more roads really mean less congestion for commuters?
- Noland, Robert & Goodwin, Phil. (2003). Building new roads really does create extra traffic: A response to Prakash et al. Applied Economics. 35. 1451-1457. 10.1080/0003684032000089872.
- Want less traffic? Build fewer roads!; Yayınlanma tarihi: 3 Eylül 2015; Kaynak site: Plus Maths. Bağlantı: Want less traffic? Build fewer roads/
- Bad Traffic? Blame Braess’ Paradox; yayınlanma tarihi: 20 Ekim 2016; Bağlantı: Bad Traffic? Blame Braess’ Paradox
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










