Kalp şeklindeki eğriler matematiksel özellikleri ve pratik uygulamaları nedeniyle yüzyıllardır matematikçileri büyülemiştir. Günümüzde de bu eğriler bir yerde sevginin sembolü haline gelmiştir. Kardiyoit veya kalp eğrisi, sabit bir çember üzerinde yuvarlanmakta olan aynı yarıçaplı ikinci bir çember üzerindeki herhangi bir noktanın izlediği eğridir. İsmi Yunanca kardia (kalp) ve eidos (şekil) kelimelerinin birleşiminden oluşur. Kalp (♥) şeklini anımsattığı için bu ismi almıştır.
Matematikte kardiyoit ismini ilk kullanan, 18. yüzyıl İtalyan matematikçisi Johann Castillon olmuştur. Bir kardiyoit, r yarıçaplı sabit bir çember etrafında kaymadan yuvarlanan, yine r yarıçaplı çemberin çevresi üzerindeki herhangi bir noktanın izlediği yol olarak tanımlanmaktadır. Bunun neye benzediğini aşağı görmeniz mümkündür.
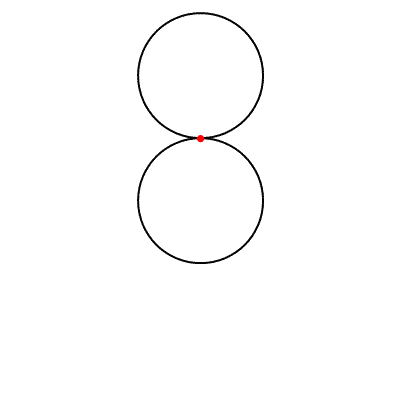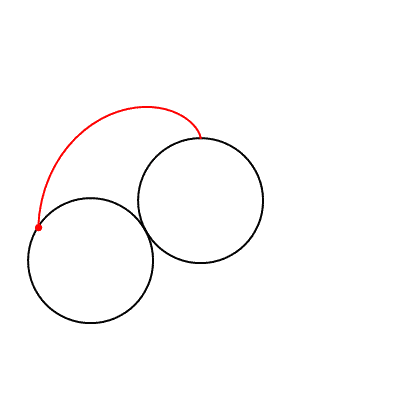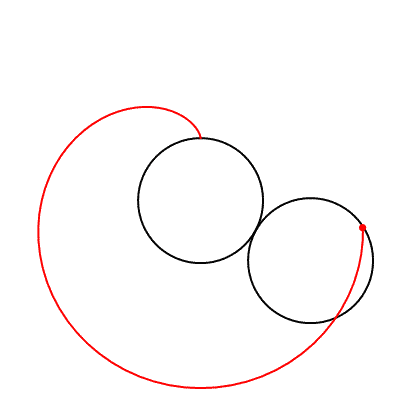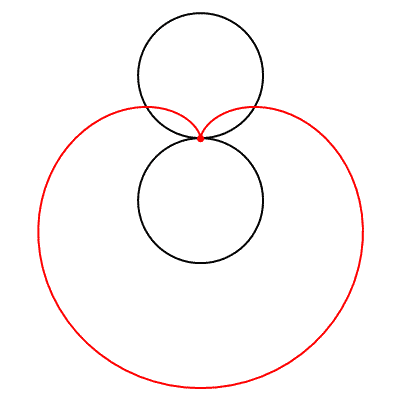
Bir kardiyoit, cebirsel olarak aşağıdaki formül ile gösterilmektedir. Kartezyen koordinat sisteminden kutupsal koordinat sistemine x=rcosθ ve y=rsinθ eşitlikleriyle geçilir. Bunun sonucunda da kardiyoit eğrisinin kutupsal koordinat sistemindeki denklemi r=1+cosθ biçiminde olur. (Eğer bu konulara aşina değilseniz bu ikilinin ne anlama geldiğini açıkladığımız bu yazımıza bakmanızı öneririz. Kartezyen mi, Kutupsal mı? Bize Hangi Koordinatlar Lazım?)
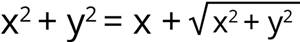
Kalp Eğrileri Örnekleri
Mathematica adlı güçlü ve çok yönlü hesaplamalı yazılım programı bilim, mühendislik ve matematikte 30 yıldan fazla bir süredir yaygın olarak kullanılmaktadır. Program bünyesinde hesaplamalarını yapabilen Wolfram Alpha adında bir sistem bulundurmaktadır. Mathematica sayısal ve sembolik hesaplamaları kolayca yapar. Bu sayede cebirsel işlemler, diferansiyel denklemler ve integraller basitleşir ve çok çeşitli grafikler kolayca çizilir. Örneğin Wolfram Alpha’da ‘kalp eğrileri’ (heart curves) biçiminde bir arama yaparsanız aşağıdaki gibi bazı grafikleri bulabilirsiniz.
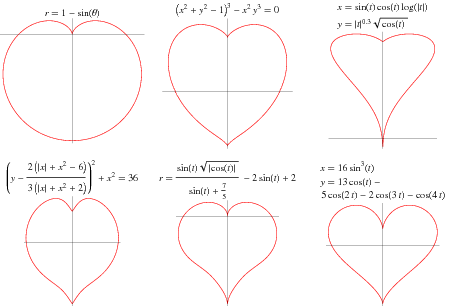
Kartografide Werner Projeksiyonu gibi bazı uygulamalarda kalp şeklindeki eğriler ortaya çıkar. Kalp eğrisinin cebirsel formu, altıncı dereceden x ve y’ye bağlı bir polinomdur. Yalnızca x’in çift dereceli kuvvetlerinden oluştuğu için, eğri simetrik bir biçimdedir.
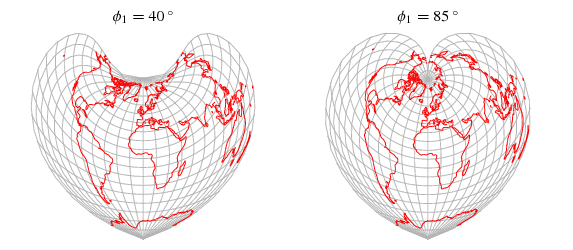
Kalp Eğrisinin Varyasyonları
Kalp eğrileri arasında yukardaki görselde ortada görebileceğiniz eğriyi ele alalım. Bu doğrunun denklemi (x2 + y2 – 1) 3 – x2y3 = 0 biçimindedir. Mathematica’daki Manipulate işlevi, bir kişinin değişen bir parametrenin etkisini keşfetmesine izin verir. Değer bir kaydırıcı aracılığıyla değiştirildiğinde, görüntülenen grafik de değişir. Biz de yukarıdaki denklemin sağ tarafını sıfırdan α değerine değiştirebiliriz. Bu durumda da ilginç başka eğriler elde ederiz.
Örneğin denklemimiz (x2 + y2 – 1) 3 – x2y3 = α biçiminde olsun. Açımız yani α değeri pozitif olacak biçimde büyüdükçe grafik, kalp biçiminden uzaklaşır. Bunun sonucunda şeklimiz giderek daireye benzemeye başlar. Bununla birlikte, α negatif biçimde arttıkça, eğri daha ilginç şekillerde değişir.
Sol ve sağda üstte loblar geliştirir ve sonunda yaklaşık α = –0.1’de bunlar ayrı kapalı eğrilere ayrılır. α <- 1.0 için eğri üzerinde hiçbir gerçek nokta yoktur ve çizim boştur. Ancak α = – 0.1 için sağ ve soldaki loblar bir çizgi film karakterinin kulakları gibi bir form alır. Sonuçta ortaya oldukça eğlenceli bir eğri çıkar.
En sevdiğiniz çizgi film karakterlerini temsil etmek için eğriler tasarlarken siz de eğlenebilirsiniz. Ayı Yogi Eğrisini Mickey Fare gibi görünecek şekilde değiştirmek biraz matematik sayesinde aslında çok da zor değildir. Ayrıca göz atmak isterseniz: Parabolik Bir Nesne Olarak Zincir Eğrisi ve Hayatımızdaki Yeri
Kaynaklar ve ileri okumalar:
- Cardioid; Bağlantı: https://byjus.com/maths/cardioid/
- Make a Cardioid Flip Book; Bağlantı: https://www.gathering4gardner.org/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak veya Patreon üzerinden ufak bir bağış yaparak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel
