Dünyadaki tüm insan kafalarında toplam kıl sayısı 1015 kadardır. Dünya’da 1023 kum tanesi olduğu ve bildiğimiz evrende yaklaşık 1081 atom olduğu düşünülmektedir. Olası satranç oyunlarının sayısı ise, tüm bu sayıların çarpımından kat kat fazladır. Yaklaşık 10120 satranç oyunu vardır ve bu sayı Shannon Sayısı olarak bilinir.

Bir maç başlamadan önce satranç taşları düzenli dizilimleri ile göz doldurur. Ancak ilk hareket, kaosa doğru bir sarmal başlatır. Birinci hamlelerin sonunda 400 olası tahta kurulumu var. İkinci hamlelerden sonra olası oyun sayısı 197.742 olur. Üçüncü hamleden sonra da bu sayı 121 milyona çıkar. Bunun sonucunda da her oyun muhtemelen daha önce hiç oynanmamış bir oyuna dönüşür.
Oyunun başında rakibinizin ilk hareketini tahmin etmek basittir. Çünkü oyuncu başlangıç dizilimi nedeniyle sadece piyonlarını ve atlarını hareket ettirecektir. Her bir piyon ve at sadece 2 konuma hareket eder. Bu durumda toplam 20 olasılık vardır. Beyaz oynadıktan sonra siyah tarafta 20 olası hareketinden birini yapar. İşte gerçek kaos bu kısımda başlar çünkü her hamle ile olasılıklar katlanır.

İlk 5 Turdaki Olası Durumlar
Öncelikle buradaki tur kavramına açıklık getirelim. 1 tur hem beyaz ve hem de siyahın hamle sonucu sonlanacaktır. Yani ilk 5 turda toplam 10 hamle yapılır. Bahsettiğimiz gibi ilk tur için olasılıkları hesaplamak zor değildir. Her oyuncu 20 hareket yaparsa ilk tur sonunda sadece olası 400 oyun oynanacaktır. İlk turun sonunda yapılan her hamleye göre ikinci tur şekillenir.
İkinci turda gelirsek oynanacak oyun sayı yaklaşık 197 bin kadar olacaktır. Sayı bir anda 400’den 197 bine çıktı. Oyunda biraz daha ileri gidip 5. turdaki toplam olası oyunların sayısına bakalım. Bu turun sonuna kadar oynanabilecek 69.352.859.712.417 olası oyun vardır.
Oyunun tümüne bakarsak karşımıza kesin cevaplar yerine yaklaşık sayılar çıkar. Bu sayılardan biri de yazının başında bahsettiğimiz “Shannon Sayısı” olur.
Shannon Sayısı Nedir?

Claude Elwood Shannon satrancın sunduğu olasılıklardan etkilenen matematikçilerden birisiydi. “How To Programme A Computer For Playing Chess“ isimli makalesinde şu soruyu sordu: ” Olası satranç oyunlarının sayısı kaçtır?”. Shannon bu soruya cevap vermek için satranç tahtasındaki oluşabilecek olası durumları incelemeye başladı.
Bu incelemeleri sonucu oyunun farkı evrelerinde sıradaki oyuncunun yaklaşık 30 farklı hamle yapabilme ihtimali olduğunu varsaydı. Bir diğer varsayımını da oyunun ortalama her tarafın yaptığı toplam 80 hareket sonrasında bitmesi üzerine yaptı. Bu sayıları kullanarak 30 80 yani yaklaşık 10 120 olası satranç oyunu olduğunu tahmin etti.
Shannon gibi bir diğer matematikçi Godfrey Hardy’nin de bu soru için bir cevabı vardı. Ona göre bu olasılık 10 üzeri 10 üzeri 50 sayısına denk gelmektedir. Bu iki tahmin birbirinden oldukça uzak tahminlerdir. Shennon’ın sayısı bu sayı yanında oldukça küçük kalmaktadır. Bu devasa farkın nedeni ise Shannon’ın varsayımlarını gerçekçi durumlar üzerine yapmış olduğundandır.
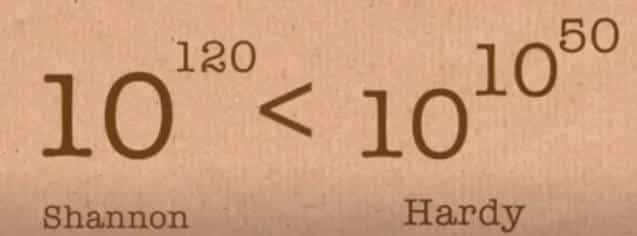
Diğer bir deyişle Shannon bir oyunun gerçekçi şekilde oynanırsa 40 tur sonunda biteceği üzerine hesaplamasını yaptı. Ancak Hardy’nin tahmini üzerine çalışması olmadığından, onun sayısının gerçeğe ne kadar uygun olduğunu bilemiyoruz.
Bu yüzden Shannon’ın sayısına bu hususta daha çok güvenebiliriz. Peki madem bu kadar fazla olasılık var. Bir satranç oyunu sonsuza kadar sürebilir mi?
Sonsuz Santranç Oyunu Mümkün Mü?
Olası hamlelerin sayısının devasa olmasına rağmen, satranç oyunundaki bazı kurallar oyunun sonsuza kadar gitmesini engeller. “50 hamle ” ve “3 kat tekrar” olarak adlandırılan bu kurallar, oyunun berabere olarak bitmesini sağlarlar.
“50 hamle” kuralına göre bir piyonun hareket etmediği ve hiçbir taşın alınmadığı art arda geçen 50 hamle olursa oyun beraberlikle sonuçlanır. “3 kat tekrar” ise oyundaki taşların 3 kez aynı konuma gelmesi yani hareketlerin tekrar etmesi durumunda uygulanır.
Sonuçta oyun yine beraberlikle sonuçlanır. Bu tür kurallar uygulanmazsa ve beraberlik durumu göz ardı edilirse sonsuza kadar sürecek bir oyun olabilir. Örneğin sadece iki şahın kaldığı bir oyun, hiçbir taraf kazanamayacağından sonsuza kadar sürecektir.
Her hamlenin binlerce belki de milyonlarca yeni olasılıklara yol açtığı bir oyunda tüm oynanacak olası hamleleri tahmin etmek bizi içinden çıkamayacağımız bir karmaşanın içine atacaktır. Çünkü Shannon sayısı olan 10120 ‘yi doğru kabul edersek, olası tüm satranç oyunlarının sayısının bilinen evrendeki atom sayısından yani 10 81‘den bile daha fazla olduğunu görürüz.
Bu durumda yapabileceğimiz, en iyi yöntem biraz daha basit düşünüp oyunun sonu yerine birkaç hamle sonrasına odaklanmak ve olasılıkların bizi götüreceği yeri beklemektir.
Kaynaklar ve ileri okumalar:
- How Many Chess Games Are Possible? This Will Blow Your Mind!; https://herculeschess.com
- How Many Different Ways Can a Chess Game Unfold?; https://www.popsci.com/
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel





