Arılar ve karıncalar gibi sosyal hayvan türlerinin gerçekten inanılmaz yetenekleri vardır. Çoğu zaman vücut boyutlarına göre oldukça büyük olan beyinleri sayesinde kendilerinden beklenmeyen ciddi ve şaşırtıcı görevlerin üstesinden gelebilirler. Bunlardan belki de en ilginci arıların peteklerinde kullandıkları hücrelerdir. Bal peteğinin altıgen formu bilim insanlarının kafasını uzun zamandır karıştırmaktadır.

Peki ama neden altıgen? Bu soruya bir cevap arayan İskenderiyeli Pappus, arıların “ilahi bir simetri duygusuna sahip olduklarını” düşündü. Marcus Terentius Varro ( MÖ 127-26) ise düzlemi döşemek için kullanılabilecek diğer çokgenlerle karşılaştırıldığında altıgenlerin en yüksek yüzey/çevre oranına sahip olduğunu düşünüyordu.
Charles Darwin ise, bal peteğini “iş gücünden ve balmumundan tasarruf etme konusunda mükemmel” bir mühendislik şaheseri olarak tanımladı. Jan Brożek (1585–1652) bu soruya cevap olarak matematiksel bir mantık öne sürdü. Sınırları en aza indirirken geniş bir bölgeyi aynı alana ait şekillerle kaplamanın en uygun yolu altıgen bir yapıyı kullanmaktı.

Bu sorun yüzyıllarca çözüme kavuşturulamadı ama sonunda 1998’de Thomas Hales tarafından kesin bir cevaba varılacaktı. Ancak o da cevabını başka bir açık problem olan Kepler Varsayımını çözdükten sonra bulacaktı. 1998 yılında kanıtlanana kadar dört yüz yıldan fazla bir süre cevabını bilemediğimiz bu teorem adını 17. yüzyıl matematikçisi ve astronom Johannes Kepler‘den ( 1571-1630) alıyordu.
Kepler Varsayımı İle Bal Peteklerinin İlgisi Nedir?
Kepler kar tanelerinin neden altıgen olduğunu sorarak işe başlamıştı. İddialarını desteklemek için bir narın içindeki nar taneleri ve arı kovanlarındaki bal petekleri gibi altıgen formdaki yapıları inceledi. Bunun devamında da bir soru sordu. Uzayda özdeş küreleri istiflemek için en etkili yol nedir?
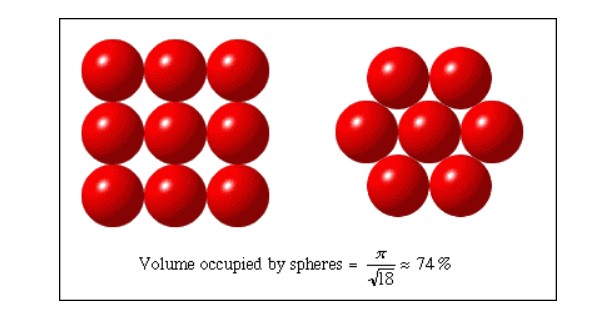
Kepler bunun manavların portakalları istifleme örneğinde gördüğümüz biçimde olması gerektiğini öne sürdü. Bu biçimde bir paketleme sonucunda yoğunluğun yaklaşık %74 olduğunu yazdı ama ispatını yapmadı. Bu problem, Carl Gauss gibi matematik devlerinin dikkatini çekti.
1900 yılında David Hilbert, Paris’teki Uluslararası Matematik Kongresi’nde yaptığı konuşmada, 20. yüzyılda matematik araştırmalarının yönünü etkileyeceğini düşündüğü problemleri tanımladı. Kepler’in Varsayımı bunun bir parçasıydı. Kepler varsayımı Thomas Hales ve öğrencisi Samuel Fargison’un bilgisayar destekli bir ispat yaptığı 1998 yılına kadar tam bir cevaba ulaşamadı.
Bal Peteğinin Altıgen Yapısı Tasarruf İçin En Etkili Formdur
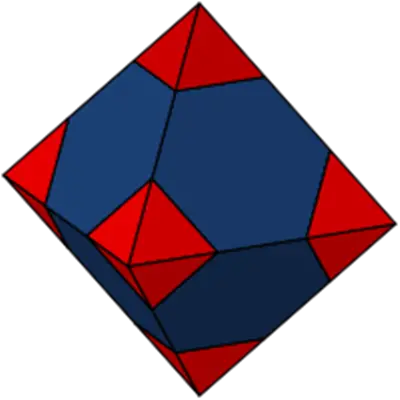
Kepler varsayımına benzer bir problem de Lord Kelvin (William Thomson) anısına Kelvin problemi diye bilinir. Bu problem de “Bir alanı minimum yüzey alanına sahip eşit hacimli hücrelere bölmenin en etkili yolu nedir?” sorusuna bir cevap arar. Lord Kelvin, 1887’de bu probleme bir çözüm önermişti ancak herhangi bir matematiksel kanıt sunmamıştı. Kendisi çözümün uzayı tetradekahedronlarla, altı kare yüzlü ve sekiz altıgen yüzlü çokyüzlülerle doldurmak olduğunu varsayıyordu.
Tüm bu bilgilerin arıların petekleri ile ne ilgisi olduğunu düşünebilirsiniz. Ancak dikkat ederseniz her iki varsayım da kullanılacak şeklin verimliliği ile ilgilidir. Tüm doğa bilimcileri, yuvarlak ve köşeli bir yapı inşa etmenin, köşeli bir yapı inşa etmekten çok daha kolay olduğunu bilir. Örneğin kuşların yuvaları bu nedenle daireseldir. Altıgen geometri ise en az yer kullanarak en sık paketlemeyi sağlayan geometridir. Bunun nedeni ile ilgili de iki olasılık bulunmaktadır.
Bunlardan ilki arıların bal peteklerini ilk dönemlerinde (büyük olasılıkla yuvarlak) yaptıkları ve zamanla, daha verimli olduğu için altıgen petek şekline geçtikleridir. Ya da arılar, peteklerini yuvarlak olacak şekilde inşa ederler. Ancak fizik kanunları gereği bu formlar kaçınılmaz olarak altıgen hale dönüşür. Belki de bu iki olasılık düzgün bir şekilde birlikte çalışmıştır. Aslında aşağıdaki videoda peteklerin altıgen yapılmadığı ancak sonrasında altıgenlere dönüştüğü görülmektedir.
Kaynaklar ve ileri okumalar:
- Karihaloo BL, Zhang K, Wang J. Honeybee combs: how the circular cells transform into rounded hexagons. J R Soc Interface. 2013 Jul 17;10(86):20130299. doi: 10.1098/rsif.2013.0299. PMID: 23864500; PMCID: PMC3730681.
- Scientists explain the amazing process by which bees make hexagonal honeycombs. Yayınlanma tarihi: 22 Temmuz 2014. Kaynak site: Discover Magazine. Bağlantı: Scientists explain the amazing process by which bees make hexagonal honeycombs/
- The Miraculous Space Efficiency of Honeycomb. Yayınlanma tarihi: 22 Temmuz 2015. Kaynak site;: Slate. Bağlantı: The Miraculous Space Efficiency of Honeycomb
Size Bir Mesajımız Var!
Matematiksel, 2015 yılından beri yayında olan ve Türkiye’de matematiğe karşı duyulan önyargıyı azaltmak ve ilgiyi arttırmak amacıyla kurulmuş bir platformdur. Sitemizde, öncelikli olarak matematik ile ilgili yazılar yer almaktadır. Ancak bilimin bütünsel yapısı itibari ile diğer bilim dalları ile ilgili konular da ilerleyen yıllarda sitemize dahil edilmiştir. Bu sitenin tek kazancı sizlere göstermek zorunda kaldığımız reklamlardır. Yüksek okunurluk düzeyine sahip bir web sitesi barındırmak ne yazık ki günümüzde oldukça masraflıdır. Bu konuda bizi anlayacağınızı umuyoruz. Ayrıca yazımızı paylaşarak da büyümemize destek olabilirsiniz. Matematik ile kalalım, bilim ile kalalım.
Matematiksel










